我所接触到的JWT

名称：JWT---》Json Web Token

用途：客户端请求服务端API时的认证方式之一

用法：

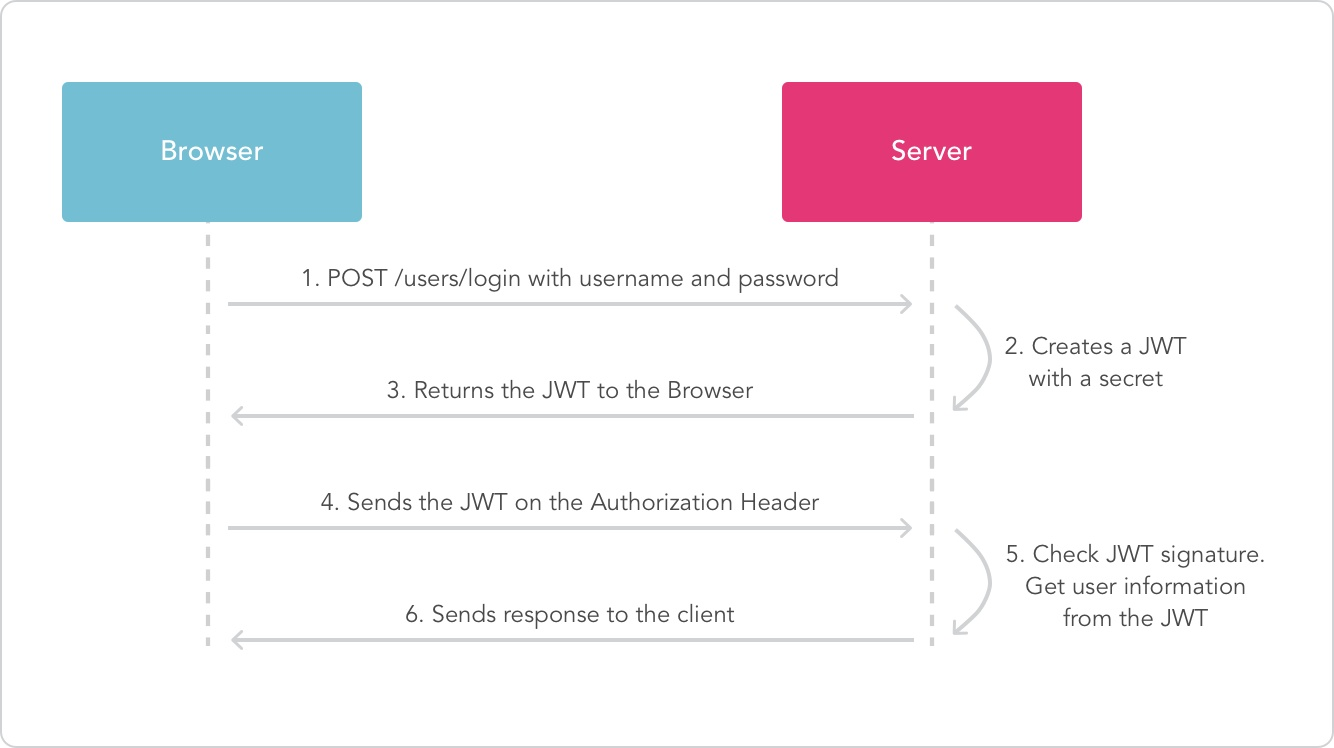
优点：

• 体积小（一串字符串），因而传输速度快

• 支持跨域验证，多应用于单点登录
• 传输方式多样，可以通过HTTP 头部（推荐）、 URL、POST 参数等方式传输
• 充分依赖无状态 API ，契合 RESTful 设计原则（无状态的 HTTP），即每个请求都是独立的

组成： header+payload+signature

header

{
  "alg": "HS256",
  "typ": "JWT"
}

payload

{
  // reserved claims
  "iss": "a.com",
  "exp": "1d",
  // public claims
  "http://a.com": true,
  // private claims
  "company": "A",
  "awesome": true
}

signature = HS256(Base64(Header) + "." + Base64(Payload), secretKey)

返回的最终结果 = Base64(Header) + "." + Base64(Payload) + "." + $Signature