Linux OpenGL 实践篇-12-procedural-texturing

程序式纹理

　　简单的来说程序式纹理就是用数学公式描述物体表面的纹路 。而实现这个过程的着色器我们称之为程序纹理着色器，通常在这类着色器中我们能使用的输入信息也就是顶点坐标和纹理坐标。

程序式纹理的优点

1.程序式纹理的内存占用比预存纹理要低的多；因为程序式纹理主要是算法的实现，数据都是通过计算产生的；

2.程序生成的纹理没有固定的面积和分辨率，可以随意的应用到不同大小的物体，而不用担心精度不够的问题；

3.程序式纹理可以写入一些算法的关键参数，可以方便的供程序修改从而创建出有趣的效果，而预存的纹理则很难进行改动；

4.如果我们使用程序式纹理计算体积而不是表面的话，那么体积的剖面表现力会比任何使用2维纹理的方式要真实的多。

程序式纹理缺点

1.程序式纹理对编程人员的要求较高，特别是算法要求；

2.程序式纹理的数据是实时计算产生的，所以每一次都需要重新计算，相对预存纹理时间会花费的比较多；

3.程序式纹理可能会带来一些难以克服的走样问题；而对于预存纹理现在的图形硬件都有比较成熟的反走样算法；

4.由于数学精度上的差异和噪声实现算法上的差异，在不同平台上程序式纹理的表现不一定一致。

简单的程序式纹理

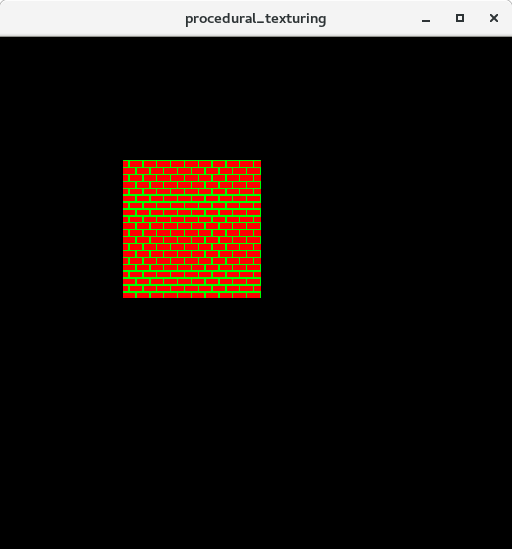
砖块

顶点着色器：

#version  core                                           

layout(location=) in vec3 iPos;
layout(location=) in vec2 iTexcoord;

uniform mat4 model;
uniform mat4 view;
uniform mat4 proj;

out vec2 texcoord;
out vec2 mcPos;

void main()
{
        texcoord = iTexcoord;
        mcPos = iPos.xy;
        gl_Position = proj * view * model * vec4(iPos,1.0);
}

片元着色器：

#version  core                                                      

in vec2 texcoord;
in vec2 mcPos;
out vec4 color;

uniform vec3 brickColor,mortarColor;
uniform vec2 brickSize;
uniform vec2 brickPct;

void main()
{
        vec2 pos, useBrick;
        pos = mcPos / brickSize;

        if(fract(pos.y * 0.5) > 0.5)
        {
                pos.x += 0.5 ;
        }

        pos = fract(pos);
        useBrick = step(pos,brickPct);

        vec3 c = mix(mortarColor,brickColor,useBrick.x * useBrick.y);
        color = vec4(c,1.0);
}

效果图：

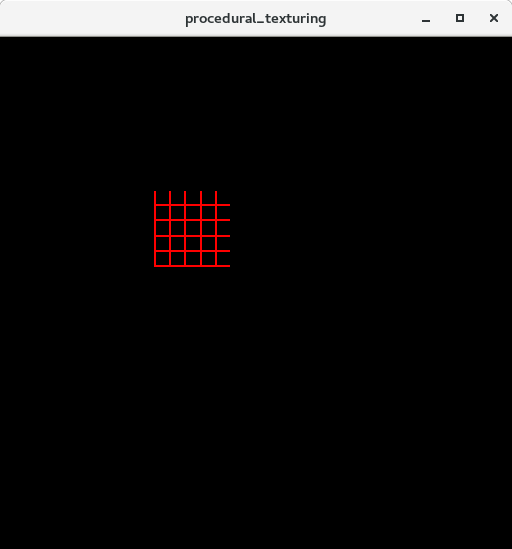
晶格

顶点着色器：

#version  core

layout(location=) in vec3 iPos;
layout(location=) in vec2 iTexcoord;                      

uniform mat4 model;
uniform mat4 view;
uniform mat4 proj;

out vec2 texcoord;

void main()
{
        texcoord = iTexcoord;
        gl_Position = proj * view * model * vec4(iPos,1.0);
}

片元着色器：

#version  core                                     

in vec2 texcoord;
out vec4 color;

uniform vec2 scale;
uniform vec2 threshold;

void main()
{
        float ss = fract(texcoord.s * scale.s);
        float tt = fract(texcoord.t * scale.t);

        if((ss > threshold.s) && (tt > threshold.t))
                discard;

        color = vec4(,,,);
}

效果图：

噪声

　　使用计算机渲染精致的物体式非常的容易的，但在真实的世界中物体往往不是这样的，它们经常是带污渍、凹痕、磨损的，如果要实现这样的效果，艺术家通常要花费很多的时间来进行构建。针对这个问题，Ken Perlin在20世纪80年代进行了深入的研究，提出了一种直到现在也很有用的技术——噪声。噪声我们可以认为是一些无规律的数据，类似老电视机中没有信号时出现的随机的雪花像素点。但这种随机的数据对于计算机图形学并没有什么用处，在计算机图形学当中，我们需要的是一种可重复的函数。比如，对于某个物体的表面，我们希望随机分布是空间上的，而不是时间上的，除非有特定的需求。根据以上的需求，理想的噪声函数应该具备下面一些重要的特性：

1.噪声不会有任何明显的规则或者重复花样；

2.噪声是一个连续函数，它的导数也是连续的；

3.噪声函数的结果可以随时间变化复现（也就是说，每一次输入的数据一致时，它返回的值也是相同的）。

4.噪声的输出数据需要一个明确的空间定义（通常是[-1,1]或[0,1]）；

5.噪声函数的小规模形式不会受到大范围的位置数据影响；

6.噪声函数是各向同性的（它的统计特性在所有的方向都是相同的）；

7.噪声可以定义为1、2、3、4或者更高维度；

8.对于任何给定的输入，噪声的计算都是非常迅速。

在OpenGL中使用以下三种方式为程序添加噪声：

1.自己实现noise函数；

2.使用内置OpenGL函数noise实现；

3.使用纹理预存噪声数据；

下面是自己实现的一个 perlin噪声函数：

/* coherent noise function over 1, 2 or 3 dimensions */
/* (copyright Ken Perlin) */

#include <stdlib.h>
#include <stdio.h>
#include <math.h>

#define B 0x100
#define BM 0xff

#define N 0x1000
#define NP 12   /* 2^N */
#define NM 0xfff

static int  p[B + B + ];
static float g3[B + B + ][];
static float g2[B + B + ][];
static float g1[B + B + ];
static int start = ;

static void init(void);

#define s_curve(t) ( t * t * (3. - 2. * t) )

#define lerp(t, a, b) ( a + t * (b - a) )

#define setup(i,b0,b1,r0,r1)\
        t = vec[i] + N;\
b0 = ((int)t) & BM;\
b1 = (b0+) & BM;\
r0 = t - (int)t;\
r1 = r0 - .;

double noise1(double arg)
{
        int bx0, bx1;
        float rx0, rx1, sx, t, u, v, vec[];

        vec[] = arg;
+---   行: if (start) {------------------------------------------------

        setup(, bx0,bx1, rx0,rx1);

        sx = s_curve(rx0);

        u = rx0 * g1[ p[ bx0 ] ];
        v = rx1 * g1[ p[ bx1 ] ];

        return lerp(sx, u, v);
}

float noise2(float vec[])
{
        int bx0, bx1, by0, by1, b00, b10, b01, b11;
        float rx0, rx1, ry0, ry1, *q, sx, sy, a, b, t, u, v;
        register int i, j;

+---   行: if (start) {----------------------------------------------------------------------

        setup(, bx0,bx1, rx0,rx1);
        setup(, by0,by1, ry0,ry1);

        i = p[ bx0 ];
        j = p[ bx1 ];

        b00 = p[ i + by0 ];
        b10 = p[ j + by0 ];
        b01 = p[ i + by1 ];
        b11 = p[ j + by1 ];

        sx = s_curve(rx0);
        sy = s_curve(ry0);

#define at2(rx,ry) ( rx * q[0] + ry * q[1] )

        q = g2[ b00 ] ; u = at2(rx0,ry0);
        q = g2[ b10 ] ; v = at2(rx1,ry0);
        a = lerp(sx, u, v);

        q = g2[ b01 ] ; u = at2(rx0,ry1);
        q = g2[ b11 ] ; v = at2(rx1,ry1);
        b = lerp(sx, u, v);

        return lerp(sy, a, b);
}

float noise3(float vec[])
{
        int bx0, bx1, by0, by1, bz0, bz1, b00, b10, b01, b11;
        float rx0, rx1, ry0, ry1, rz0, rz1, *q, sy, sz, a, b, c, d, t, u, v;
        register int i, j;

+---   行: if (start) {------------------------------------------------------------

        setup(, bx0,bx1, rx0,rx1);
        setup(, by0,by1, ry0,ry1);
        setup(, bz0,bz1, rz0,rz1);

        i = p[ bx0 ];
        j = p[ bx1 ];

        b00 = p[ i + by0 ];
        b10 = p[ j + by0 ];
        b01 = p[ i + by1 ];
        b11 = p[ j + by1 ];

        t  = s_curve(rx0);
        sy = s_curve(ry0);
        sz = s_curve(rz0);

#define at3(rx,ry,rz) ( rx * q[0] + ry * q[1] + rz * q[2] )

        q = g3[ b00 + bz0 ] ; u = at3(rx0,ry0,rz0);
        q = g3[ b10 + bz0 ] ; v = at3(rx1,ry0,rz0);
        a = lerp(t, u, v);

        q = g3[ b01 + bz0 ] ; u = at3(rx0,ry1,rz0);
        q = g3[ b11 + bz0 ] ; v = at3(rx1,ry1,rz0);
        b = lerp(t, u, v);

        c = lerp(sy, a, b);

        q = g3[ b00 + bz1 ] ; u = at3(rx0,ry0,rz1);
        q = g3[ b10 + bz1 ] ; v = at3(rx1,ry0,rz1);
        a = lerp(t, u, v);

        q = g3[ b01 + bz1 ] ; u = at3(rx0,ry1,rz1);
        q = g3[ b11 + bz1 ] ; v = at3(rx1,ry1,rz1);
        b = lerp(t, u, v);

        d = lerp(sy, a, b);

        return lerp(sz, c, d);
}

static void normalize2(float v[])
{
        float s;

        s = sqrt(v[] * v[] + v[] * v[]);
        v[] = v[] / s;
        v[] = v[] / s;
}

static void normalize3(float v[])
{
        float s;

        s = sqrt(v[] * v[] + v[] * v[] + v[] * v[]);
        v[] = v[] / s;
        v[] = v[] / s;
        v[] = v[] / s;
}

static void init(void)
{
        int i, j, k;

        for (i =  ; i < B ; i++) {
                p[i] = i;

                g1[i] = (float)((random() % (B + B)) - B) / B;

                for (j =  ; j <  ; j++)
                        g2[i][j] = (float)((random() % (B + B)) - B) / B;
                normalize2(g2[i]);

                for (j =  ; j <  ; j++)
                        g3[i][j] = (float)((random() % (B + B)) - B) / B;
                normalize3(g3[i]);
        }

        while (--i) {
                k = p[i];
                p[i] = p[j = random() % B];
                p[j] = k;
        }

        for (i =  ; i < B +  ; i++) {
                p[B + i] = p[i];
                g1[B + i] = g1[i];
                for (j =  ; j <  ; j++)
                        g2[B + i][j] = g2[i][j];
                for (j =  ; j <  ; j++)
                        g3[B + i][j] = g3[i][j];
        }
}

顶点着色器：

#version  core

uniform mat4 MVMat;
uniform mat4 MVPMat;
uniform mat4 normalMat;

uniform vec3 lightPos;
uniform float scale;

layout(location = )in vec3 iPos;
layout(location = )in vec3 iNormal;

out float lightIntensity;
out vec3 mcPos;

void main()
{
        vec3 ecPos = vec3(MVMat * vec4(iPos,));
        mcPos = iPos * scale;
        vec3 tnorm = normalize(vec3(normalMat * vec4(iNormal,1.0)));
        vec3 lpos = vec3(MVMat * vec4(lightPos,1.0));
        lightIntensity = dot(normalize(lpos - ecPos),tnorm);
        lightIntensity *= 1.5f;
        gl_Position = MVPMat * vec4(iPos,);
}

片元着色器：

#version  core

uniform sampler3D noise;
uniform vec3 skyColor;
uniform vec3 cloudColor;

in float lightIntensity;
in vec3 mcPos;

out vec4 color;

void main()
{
        vec4 noisevec = texture(noise,mcPos);
        float intensity = (noisevec[] + noisevec[] + noisevec[] + noisevec[] + 0.03125) * 1.5;

        vec3 c = mix(skyColor,cloudColor,intensity) * lightIntensity;
        color = vec4(c,1.0);
}

效果图：

实践源代码：https://github.com/xin-lover/opengl-learn/tree/master/chapter-12-procedural_texturing