[SDOI2015][bzoj3994] 约数个数和 [莫比乌斯反演]

题面：

传送门

思路：

首先，我们需要证明一个结论：d(i*j)等于sigma(gcd(x,y)==1)，其中x为i的约数，y为j的约数

对于nm的每一个质因子pi分别考虑，设n = pi^ai + n'，m = pi^bi + m'

那么显然质因子pi对d(nm)的贡献为(ai+bi+1)

同理，考虑右边的式子，我们发现质数pi对右侧做的贡献仍然是(ai+bi+1)，即如下的(x,y)

(pi^ai,1) (pi^(ai-1),1) ..... (1,1) .....(1,pi^(bi-1)) (1,pi^bi)

因此左右两式相同

因此原待求表达式化为如下形式：

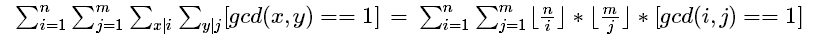
由莫比乌斯函数第二情况得：上式可化为

其中g(i)表示前半个式子中的那段东西，相当于d(i)的前缀和

于是O(Tsqrt(min(n,m))轻松解决

顺便说一句，求约数个数也有线性的方法

记录c[i]表示i的最小的质因子的次数

每次更新这个，然后同时用c[i]+1更新d[i*pri[j]]即可

Code：

 #include<iostream>
 #include<cstdio>
 #include<cstring>
 #include<algorithm>
 #define ll long long
 using namespace std;
 inline ll read(){
     ll re=,flag=;char ch=getchar();
     while(ch>''||ch<''){
         if(ch=='-') flag=-;
         ch=getchar();
     }
     while(ch>=''&&ch<='') re=(re<<)+(re<<)+ch-'',ch=getchar();
     return re*flag;
 }
 ll mu[],pri[],c[],d[],cnt;bool vis[];
 void init(ll n){
     mu[]=d[]=c[]=;ll i,j,k;
     for(i=;i<=n;i++){
         if(!vis[i]){
             pri[++cnt]=i;mu[i]=-;c[i]=;d[i]=;
         }
         for(j=;(j<=cnt)&&(i*pri[j]<=n);j++){
             k=i*pri[j];vis[k]=;
             if(i%pri[j]==){
                 d[k]=d[i]/(c[i]+)*(c[i]+);
                 c[k]=c[i]+;break;
             }
             mu[k]=-mu[i];
             d[k]=d[i]*d[pri[j]];c[k]=;
         }
     }
     for(i=;i<=n;i++) mu[i]+=mu[i-];
     for(i=;i<=n;i++) d[i]+=d[i-];
 }
 ll n,m;
 int main(){
     ll i,j,T=read(),ans;init();
     while(T--){
         n=read();m=read();ans=;
         if(n>m) swap(m,n);
         for(i=;i<=n;i=j+){
             j=min(n/(n/i),m/(m/i));
             ans+=(mu[j]-mu[i-])*d[n/i]*d[m/i];
         }
         printf("%lld\n",ans);
     }
 }