UVA10410 TreeReconstruction 树重建 （dfs，bfs序的一些性质，以及用栈处理递归 ）

题意，给你一颗树的bfs序和dfs序，结点编号小的优先历遍，问你可能的一种树形；

输出每个结点的子结点。

注意到以下事实：

（1）dfs序中一个结点的子树结点一定是连续的。

（2）bfs，dfs序中的一个结点u的后续结点一定是u或u的后兄弟结点{v}，或u和{v}的后代节点{s}。

（3）如果有后兄弟结点，那么bfs序中u后面紧跟着的一定是第一后兄弟结点v1，

（4）如果有后代结点，那么dfs序中u后面紧跟着的一定是第一个子结点s1。

记结点u的bfs序记为bfs(u)，dfs序记为dfs(v)；

dfs序中，一个结点u，结点为v满足dfs(v) = dfs(u) + 1，如果bfs(v) = bfs(u)+1 且 v > u；那么v一定可以视作u的第一个后兄弟结点，

如果不成立，那么v是u的子节点，可以推出u是bfs中u所在层的最后一个结点，这时候u没有后兄弟结点，所以后面的结点一定都是他的后代结点，那么v就一定可以等效作u的兄弟结点而不改变bfs，dfs序。

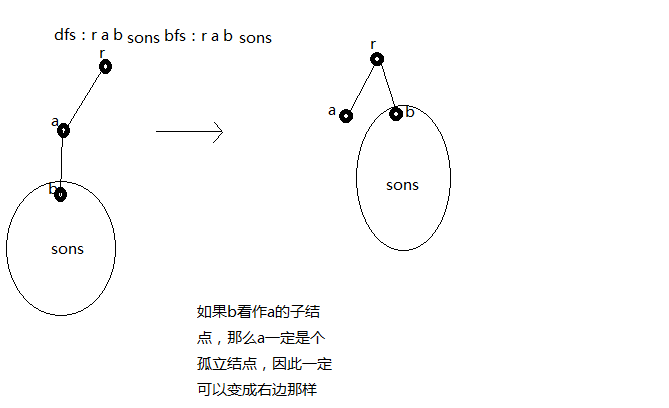
到此，（5）满足bfs(v) = bfs(u)+1 且 v > u条件的v看作是u的第一个后兄弟结点，不满足这个条件的一定不是后兄弟结点，这个可以根据定义可证。

如果v满足（5），根据（1），u以及子树就访问完了，如果v不满足条件且bfs（v）>bfs(u) + 1那么v一定是u的子结点，如果bfs（v）<bfs(u)那么说明v是其父辈结点，而且u的子树已经访问完了。

迭代上述过程，用栈辅助完成，边界条件是root，大功告成~

学习点：

1.用栈处理递归过程。

2.bfs，dfs线性序列的性质。

原来树形转线性要用到这些性质

// Rey
#include<bits/stdc++.h>
using namespace std;
const int maxn = +;

vector<int> G[maxn];
int pos[maxn];

int main()
{
 //  freopen("in.txt","r",stdin);
   int n;
   int t;
   while(~scanf("%d",&n)&&n){
      for(int i = ; i <= n; i++)
         scanf("%d",&t), pos[t] = i, G[i].clear();
      int root;
      scanf("%d",&root);
      stack<int> sta;
      sta.push(root);
      for(int i = ; i < n; i++){
         scanf("%d",&t);
         for(;;) {
            int u = sta.top();if( pos[u]+ < pos[t] ||  (pos[u]+ == pos[t] && u > t) || u == root  ) {
               G[u].push_back(t);
               sta.push(t);
               break;
            }else {
               sta.pop();
            }
         }

      }
      for(int i = ; i <= n; i++) {
         printf("%d:",i);
         for(int j = , sz =  G[i].size(); j < sz; j++)
            printf(" %d",G[i][j]);
         puts("");
      }
   }
   return ;
}