python算法-汉诺塔问题

汉诺塔问题

 

初始状态：

思考：当盘子的个数是3的时候，大家写出移动顺序

移动的步骤：

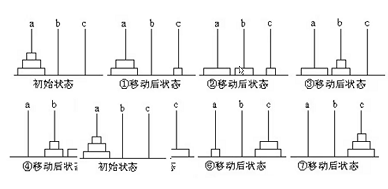
3个盘子，从a到c

1、前面两个盘子，从a到b

1）把前面一个盘子，从a到c

a->c

2）把第二个盘子，从a到b

a->b

3）把c上的盘子，从c到b

c->b

2、最后一个盘子，从a到c

a->c

3、把b上的两个盘子，从b到c

1）把前面一个盘子，从b到a

b->a

2）把第二个盘子，从b到c

b->c

3）把a上的盘子，从a到c

a->c

总结：

n个盘子，从a到c

1、n-1个盘子从a到b

2、最后一个盘子，从a到c

3、n-1个盘子从b到c

代码实现：

# encoding=utf-8

def hanoi(n,a,b,c):

    if n == 1:

        print a,'->',c

    else:

        hanoi(n-1,a,c,b)

        hanoi(1,a,b,c)

        hanoi(n-1,b,a,c)

if __name__ == '__main__':

    hanoi(3,'a','b','c')