HDU4990 Reading comprehension —— 递推、矩阵快速幂

题目链接：https://vjudge.net/problem/HDU-4990

Reading comprehension

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 2329    Accepted Submission(s): 954

Problem Description

Read the program below carefully then answer the question.
#pragma comment(linker, "/STACK:1024000000,1024000000")
#include <cstdio>
#include<iostream>
#include <cstring>
#include <cmath>
#include <algorithm>
#include<vector>

const int MAX=100000*2;
const int INF=1e9;

int main()
{
  int n,m,ans,i;
  while(scanf("%d%d",&n,&m)!=EOF)
  {
    ans=0;
    for(i=1;i<=n;i++)
    {
      if(i&1)ans=(ans*2+1)%m;
      else ans=ans*2%m;
    }
    printf("%d\n",ans);
  }
  return 0;
}

 

Input

Multi test cases，each line will contain two integers n and m. Process to end of file.
[Technical Specification]
1<=n, m <= 1000000000

 

Output

For each case，output an integer，represents the output of above program.

 

Sample Input

1 10
3 100

 

Sample Output

1
5

 

Source

BestCoder Round #8

 

Recommend

heyang

题解：

当n为奇数时，f[n] = 2*f[n-1]+1，f[n-1] = 2*f[n-2]，所以：f[n] = f[n-1] + 2*f[n-2] + 1;

当n为偶数时，f[n] = 2*f[n-1]，f[n-1] = 2*f[n-2] + 1，所以：f[n] = f[n-1] + 2*f[n-2] + 1;

综上：f[n] = f[n-1] + 2*f[n-2] + 1，构造矩阵：

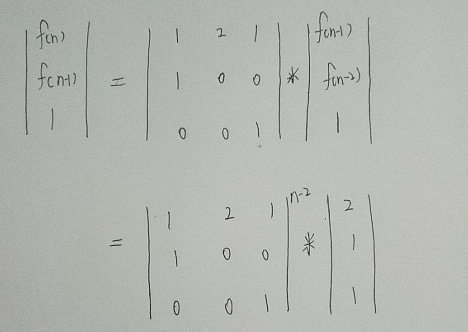
代码如下：

 #include <iostream>
 #include <cstdio>
 #include <cstring>
 #include <algorithm>
 #include <vector>
 #include <cmath>
 #include <queue>
 #include <stack>
 #include <map>
 #include <string>
 #include <set>
 using namespace std;
 typedef long long LL;
 const int INF = 2e9;
 const LL LNF = 9e18;
 //const int MOD = 10000007;
 const int MAXN = 1e6+;

 LL MOD;
 const int Size = ;
 struct MA
 {
     LL mat[Size][Size];
     void init()
     {
         for(int i = ; i<Size; i++)
         for(int j = ; j<Size; j++)
             mat[i][j] = (i==j);
     }
 };

 MA mul(MA x, MA y)
 {
     MA ret;
     memset(ret.mat, , sizeof(ret.mat));
     for(int i = ; i<Size; i++)
     for(int j = ; j<Size; j++)
     for(int k = ; k<Size; k++)
         ret.mat[i][j] += (1LL*x.mat[i][k]*y.mat[k][j])%MOD, ret.mat[i][j] %= MOD;
     return ret;
 }

 MA qpow(MA x, LL y)
 {
     MA s;
     s.init();
     while(y)
     {
         if(y&) s = mul(s, x);
         x = mul(x, x);
         y >>= ;
     }
     return s;
 }

 MA tmp = {
     , , ,
     , , ,
     , ,
 };

 int main()
 {
     LL n, m;
     while(scanf("%lld%lld",&n,&m)!=EOF)
     {
         MOD = m;
         if(n<=)
         {
             printf("%lld\n", n%MOD);
             continue;
         }

         MA s = tmp;
         s = qpow(s, n-);

         LL ans = ((2LL*s.mat[][]%MOD + s.mat[][])%MOD+s.mat[][])%MOD;
         printf("%lld\n", ans);
     }
 }