BZOJ1018：[SHOI2008]堵塞的交通

浅谈树状数组与线段树：https://www.cnblogs.com/AKMer/p/9946944.html

题目传送门：https://www.lydsy.com/JudgeOnline/problem.php?id=1018

我们把第一行和第二行的城市一起处理，对于每一个区间[\(l,r\)]的城市，我们需要维护下面六种关系：

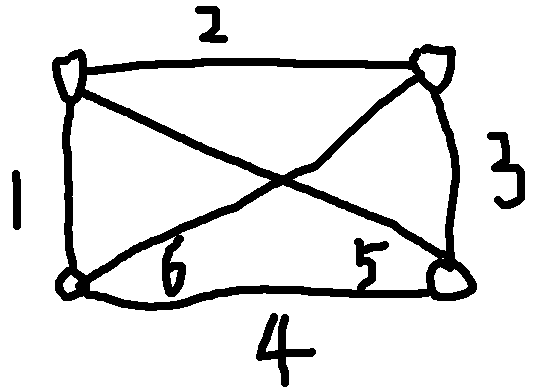
一共六条边，分别用\(bool\)类型的六个变量来表示这六种联通关系是否成立。

然后询问两个城市是否联通，也许他们会绕出区间[\(l,r\)]再绕回来然后联通，所以有四种路径可以走；假设我询问的是一号城市和三号城市，二号城市是一号城市上方/下方的城市，四号城市是三号城市上方/下方的城市，那么这四条路径分别是：

一号---->三号（红色）

一号----》二号---->三号（绿色）

一号---->四号----》三号（蓝色）

一号----》二号---->四号----》三号（灰色）

其中>表示在区间内，》表示绕出去，如图所示：

时间复杂度：\(O(nlong)\)

空间复杂度：\(O(n)\)

代码如下：

#include <cstdio>
#include <algorithm>
using namespace std;

const int maxn=1e5+5;

int n;
char s[10];
bool bo[maxn*3];//bo数组里，[1,n-1]存的是第一行的道路，[n,2*n-1]存的是每一列的道路，[2*n,3*n-2]存的是第二行的道路。

int read() {
	int x=0,f=1;char ch=getchar();
	for(;ch<'0'||ch>'9';ch=getchar())if(ch=='-')f=-1;
	for(;ch>='0'&&ch<='9';ch=getchar())x=x*10+ch-'0';
	return x*f;
}

struct tree_node {
	bool a1,a2,a3,a4,a5,a6;
};

struct segment_tree {
	tree_node tree[maxn<<2];

	tree_node merge(tree_node f,tree_node g,int mid) {
		tree_node res;int mid1=mid,mid2=mid+2*n-1;
		res.a1=(f.a1)|(f.a2&&bo[mid1]&&g.a1&&bo[mid2]&&f.a4);
        //f.a2&&bo[mid1]&&g.a1&&bo[mid2]&&f.a4  1号路径
        //f.a5&&bo[mid2]&&g.a1&&bo[mid1]&&f.a6  2号路径
        //如果2号路径存在那么1号路径必然存在，所以只需要判1号路径即可
		res.a2=(f.a2&&bo[mid1]&&g.a2)|(f.a5&&bo[mid2]&&g.a6);
		res.a3=(g.a3)|(g.a2&&bo[mid1]&&f.a3&&bo[mid2]&&g.a4);
		res.a4=(f.a4&&bo[mid2]&&g.a4)|(f.a6&&bo[mid1]&&g.a5);
		res.a5=(f.a2&&bo[mid1]&&g.a5)|(f.a5&&bo[mid2]&&g.a4);
		res.a6=(f.a4&&bo[mid2]&&g.a6)|(f.a6&&bo[mid1]&&g.a2);
		return res;
	}

	void build(int p,int l,int r) {
		if(l==r) {
			tree[p].a2=tree[p].a4=1;
			return;
		}
		int mid=(l+r)>>1;
		build(p<<1,l,mid);
		build(p<<1|1,mid+1,r);
	}

	void change(int p,int l,int r,int L,int R) {
		if(l==r) {
			if(L==R) {
				tree[p].a1^=1;
				tree[p].a3^=1;
				tree[p].a5^=1;
				tree[p].a6^=1;//如果是单点修改那么这四种关系应该改变状态
			}
			return;
		}
		int mid=(l+r)>>1;
		if(L<=mid)change(p<<1,l,mid,L,R);
		else change(p<<1|1,mid+1,r,L,R);
		tree[p]=merge(tree[p<<1],tree[p<<1|1],mid);
	}

	tree_node query(int p,int l,int r,int L,int R) {
		if(L<=l&&r<=R)return tree[p];
		int mid=(l+r)>>1;tree_node res;
		if(R<=mid)res=query(p<<1,l,mid,L,R);
		else if(L>mid)res=query(p<<1|1,mid+1,r,L,R);
		else res=merge(query(p<<1,l,mid,L,R),query(p<<1|1,mid+1,r,L,R),mid);
		return res;
	}
}T;

int main() {
	n=read();T.build(1,1,n);
	while(~scanf("%s",s+1)) {
		if(s[1]=='E')break;
		int x1=read(),y1=read(),x2=read(),y2=read();
		if(y1>y2)swap(y1,y2),swap(x1,x2);
		if(s[1]=='O'||s[1]=='C') {
			if(x1==x2) {
				int tmp=y1;
				if(x1==2)tmp+=2*n-1;
				bo[tmp]^=1;T.change(1,1,n,y1,y2);
			}
			else {
				bo[y1+n-1]^=1;
				T.change(1,1,n,y1,y2);
			}
		}
		else {
			bool ans=0;
			tree_node j=T.query(1,1,n,1,y1);
			tree_node k=T.query(1,1,n,y1,y2);
			tree_node l=T.query(1,1,n,y2,n);
			if(x1==x2) {
				if(x1==1) {
					ans|=k.a2;
					ans|=j.a3&&k.a6;
					ans|=k.a5&&l.a1;
					ans|=j.a3&&k.a4&&l.a1;
				}
				else {
					ans|=k.a4;
					ans|=j.a3&&k.a5;
					ans|=k.a6&&l.a1;
					ans|=j.a3&&k.a2&&l.a1;
				}
			}
			else {
				if(x1==1) {
					ans|=k.a5;
					ans|=j.a3&&k.a4;
					ans|=k.a2&&l.a1;
					ans|=j.a3&&k.a6&&l.a1;
				}
				else {
					ans|=k.a6;
					ans|=j.a3&&k.a2;
					ans|=k.a4&&l.a1;
					ans|=j.a3&&k.a5&&l.a1;
				}
			}//对于询问的两个点的位置一共有四种不同的关系，分别分情况讨论
			if(ans)puts("Y");
			else puts("N");
		}
	}
	return 0;
}