B树——思路、及C语言代码的实现
0.序
本人现读本科大二，这学期学习数据结构，老师为我们的期末作业布置一道任选题，而我一直以来都有听说B树是一棵挺神奇的树，所以我选择了它，当然更重要的原因是因为B树的难度最高，我喜欢做有挑战性的工作。同时，我听我基友说他热衷于将自己所学所想分享到博客园上，故才有了这样一篇文章。希望我能够在写博客的同时学习到更多东西，同时也能帮助到其他遇到或者即将遇到雷同问题的初学者们。
1.关于B树
B树是一种称之为查找树的树，与之类似的有查找二叉树，平衡二叉树，除此之外，还有各种B树的兄弟姐妹B+树、B-树、B*树等，他们共同的特点就是都是按照一定的顺序规律存储的。B树的应用也是很广泛的，B树是几乎所有数据库的默认索引结构，也是用的最多的索引结构。B树是一种多叉树，根据其最多叉的数目可以直接称为M阶B树。根据算法导论上叙述，还可按B树每个节点最少的分支确定一棵B树的阶，但是这样的话B树的阶便必须为偶数。我个人是使用根据最大分支的数目确定B树的阶的。
下图就是某一棵B树，每一个结点中都包含有数个数据元素，而同时一定会有数据元素的个数加一个的子树。
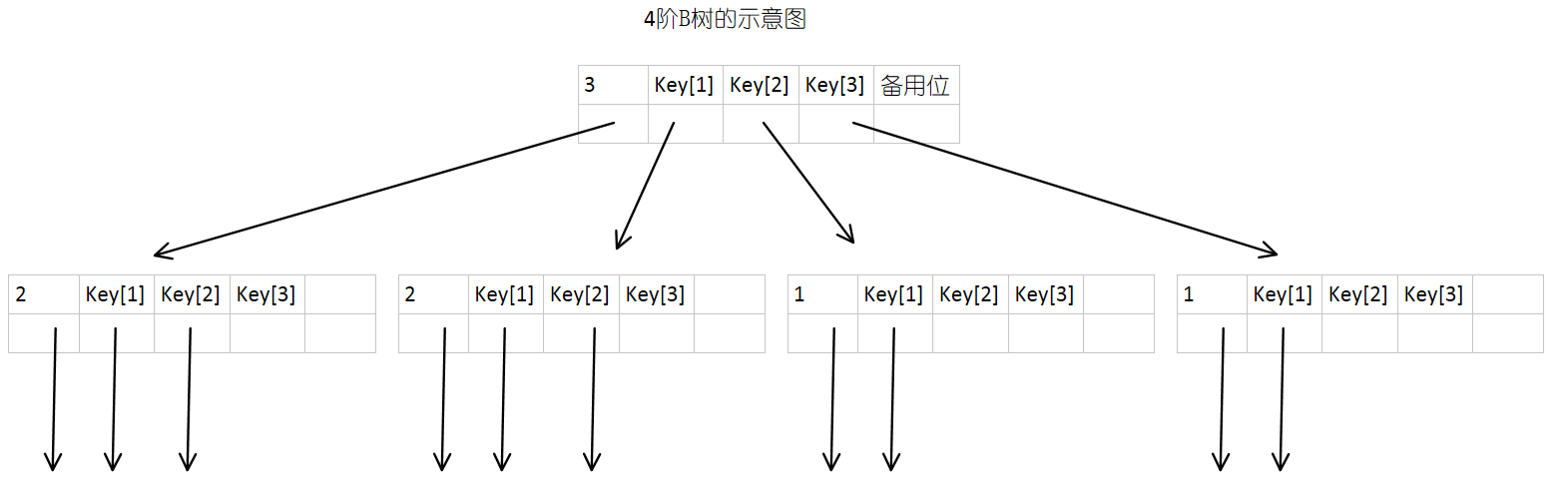
一棵M阶B树或为空树，或为满足下列特性的M叉树：
（1）树中每个结点最多含有M棵子树；
（2）若根结点不是叶子结点，则至少有2棵子树；
（3）除根结点之外的所有非终端结点至少有[m/2]棵子树；
（4）每个非终端结点中包含的信息keynum，ptr[0],key[1],ptr[1],key[2],ptr[2],……key[keynum],ptr[keynum];
其中，key为关键字，且关键字按升序排序，ptr为指向子树的根结点指针
2.思路及实现
B树的接口主要是插入（包括空树插入一个元素）和删除操作，而插入和删除操作不可避免的都会用到查找操作，而查找的主要思路比较简单，主要是利用B树是一种排序树的原理，可以很快找到要插入位置或者要删除结点。这里的关键是注意返回内容包括查找结果所在结点，以及该元素所在位置，这是为了方便接下来的操作比较简单。
插入：
通过对B树进行遍历，找出要插入的结点以及结点位置，如果找到的key值在B树当中已经存在，则说明插入失败，否则，就可以进行插入操作。这里可以先不管是否超出M阶树的上限要求，因为我们在定义的时候会故意留下一个位置，可以存放多余的一个元素，插入之后，通过判断是否达到M阶树上限要求，再进行递归的分裂操作。
/***
* @name Status insertBTree(BTree &T, Record e)
* @description 插入实现元素的插入
* @return 成功返回OK,如果存在则返回FALSE，否则返回ERROR
* @notice
***/
Status insertBTree(BTree &T, Record e)
{
BTree p;
int index, temp;
Status find_flag;
if (NULL == T)//考虑B树为空树的情况
{
T = (BTree)malloc(BTLEN);
if (NULL == T) return OVERFLOW;
T->keynum = ;
T->parent = NULL;
for (index = ;index <= m; ++index)
{
T->ptr[index] = NULL;
T->key[index] = ;
}
T->key[] = e.key;
return OK;
}
find_flag = findBTree(T, p, temp, e.key);//寻找插入节点
if (find_flag == TRUE)
{
return FALSE;
}
if (find_flag == FALSE)
{ //不管怎样先直接插入
p->keynum++;
for (index = p->keynum;index > temp;--index)
{
p->key[index] = p->key[index - ];
p->ptr[index] = p->ptr[index - ];
}
p->ptr[temp] = NULL;
p->key[temp] = e.key;
if (p->keynum == m) //这种情况得分裂
{
splitBTree(p);
}
renewParent(T);
return OK;
}
return ERROR;
}
分裂：
分裂操作是插入操作过程中一个最重要的操作，因为这是处理“冲突”（即结点中的数据元素大于B树规则中要求的最大个数）的一个通用的处理方式，这种方式必须要对所有的情况都适用，而分裂是解决这一问题一个方法。当然这种方法只是考虑到效率，没有对兄弟可否借数据进行判断，但是另外一种方式比较麻烦，这里先不做讨论。
分裂的思路是让父亲结点先腾出一个位置（包括key和ptr）出来，然后在需要分裂的结点里面取中间的元素并且移动中间的元素key到父亲结点已经腾出来的key位置那里，然后把分裂出来的右部分接到腾出来的ptr那里。注意整个过程对左部分和右部分的都要改变元素的个数以及清空一些没用的空间。在往上分裂之后可能会造成一种情况，就是父亲结点也可能达到分裂的最大个数，所以，检查父亲结点是否需要分裂，需要的话，递归之。
/***
* @name status splitBTree(BTree T)
* @description 递归实现分裂节点操作
* @return 成功返回OK,否则返回ERROR
* @notice
***/
Status splitBTree(BTree T) //此时分裂的节点一定会是超出最大值的。
{
BTree t1, t2;
int index, index_1;
if (T->parent == NULL)
{
t1 = (BTree)malloc(BTLEN);
if (NULL == t1) return OVERFLOW;
t2 = (BTree)malloc(BTLEN);
if (NULL == t2) return OVERFLOW; t1->keynum = m / ;
t2->keynum = m - (m / ) - ;
t1->parent = T;
t2->parent = T;
for (index = ;index <= m; ++index) //先全部初始化
{
t1->ptr[index] = NULL;
t1->key[index] = ;
t2->ptr[index] = NULL;
t2->key[index] = ;
}
for (index = ;index <= m / ; ++index) //初始化t1
{
t1->ptr[index] = T->ptr[index];
t1->key[index] = T->key[index];
}
t2->ptr[] = T->ptr[(m / ) + ];
for (index = (m / ) + ;index <= m; ++index) //初始化t2
{
t2->ptr[index - ((m / ) + )] = T->ptr[index];
t2->key[index - ((m / ) + )] = T->key[index];
}
T->keynum = ;
T->ptr[] = t1;
T->ptr[] = t2;
T->key[] = T->key[m / + ];
for (index = ;index <= m; ++index) //初始化T
{
T->ptr[index] = NULL;
T->key[index] = ;
}
return OK;
}
删除：
B树元素的删除操作与插入操作类似，但是却要麻烦，因为得分两种情况处理。（1）寻找到存在这个元素，而且这个元素所在是叶子节点（即它的孩子为空），直接对其进行删除，之后再判断是否小于B树规则中要求的最小的子树个数。如果小于，那就调用合并函数。（2）如果寻找到的这个元素是非叶子节点的元素，通过寻找比该元素小的最大元素（该元素肯定为叶子节点），把该元素直接赋值给要删除的元素，再在叶子节点处进行（1）中的操作。
/***
* @name Status deleteBTreeRecord(BTree &T, Record e)
* @description 实现B树元素的删除
* @return 成功返回OK,否则返回ERROR
* @notice
***/
Status deleteBTreeRecord(BTree &T, Record e)
{
BTree p, q;
int num, temp, index;
Status find_flag;
if (T == NULL)
return ERROR;
find_flag = findBTree(T, p, temp, e.key);
if (find_flag == FALSE)
{
return FALSE;
}
if (find_flag == TRUE)
{
//deleteBTreeBNode(p,temp);
if (p->ptr[temp] == NULL) //如果是叶子节点的话
{
for (index = temp;index <= p->keynum;++index)
{
p->key[index] = p->key[index + ];
p->ptr[index] = p->ptr[index + ];
}
p->keynum--;
if (p->keynum == (m + ) / - )
{
//调用借兄弟的函数
if (borrowBNode(p) == EMPTY) T = NULL;
else renewParent(T);
}
return OK;
}
else //不是叶子结点的话
{
//遍历
findMax(p->ptr[temp - ], q, num);//返回的q一定会是叶子节点
p->key[temp] = q->key[num];
q->key[num] = ;
q->keynum--;
if (q->keynum == (m + ) / - )
{
//调用借兄弟的函数
if (borrowBNode(q) == EMPTY) T = NULL;
else renewParent(T);
}
return OK;
}
return OK;
}
return ERROR;
}
合并:
在此先声明，因为一开始只考虑B树的阶为4的情况，后来改为使用宏定义阶M的数值，所以这段代码存在BUG，只支持阶为3或4的B树= =。
思路还是挺清晰的，首先先向兄弟结点借元素，如果兄弟能够借给你元素的话（即借了你之后并不会小于最少的分支），那么直接从兄弟那里取元素，否则，和兄弟合并。
合并其实是分裂反过来的情况，从父亲结点那里取出一个key值介于要合并的两个结点之间的元素，插入左部分最末尾处，同时右部分插到左部分后面，然后父亲结点元素依次往前挪。从而实现合并操作。之后，也必须对父亲结点进行判断是否小于最小的分支数，如果也小于，对父亲节点进行递归操作。
/***
* @name Status borrowBNode(BTree &T)
* @description 递归实现，向兄弟借元素，否则和兄弟合并
* @return 成功返回OK,否则返回ERROR
* @notice 这种情况应该是T为单元素结点
***/
Status borrowBNode(BTree T)
{
int mynum, bronum, index;
BTree b = NULL, f = NULL;
if (T == NULL) return ERROR;
f = T->parent;
if (f == NULL)//考虑父亲结点不存在的情况
{
if (T->keynum == )
{
f = T->ptr[];
if (f == NULL)
{
free(T);
return EMPTY;
}
for (index = ;index <= f->keynum;index++)
{
T->key[index] = f->key[index];
T->ptr[index] = f->ptr[index];
}
T->keynum = f->keynum;
free(f);
renewParent(T);
}
return OK;
}
mynum = whichSon(T);
if (mynum == )
bronum = ;
else
bronum = mynum - ;
b = f->ptr[bronum];
if (b->keynum == (m + ) / - ) //如果兄弟帮不了你了
{
//那么就和这个兄弟合体
if (bronum < mynum) //如果我不是第一个
{
b->keynum++;
b->key[b->keynum] = f->key[mynum];
b->ptr[b->keynum] = T->ptr[];
for (index = ;index <= T->keynum;index++)
{
b->key[index + b->keynum] = T->key[index];
b->ptr[index + b->keynum] = T->ptr[index];
b->keynum++;
}
free(T);
for (index = mynum;index <= f->keynum;index++)
{
f->key[index] = f->key[index + ];
f->ptr[index] = f->ptr[index + ];
}
f->keynum--;
}
else
{
T->keynum++;
T->key[T->keynum] = f->key[bronum];
T->ptr[T->keynum] = b->ptr[];
for (index = ;index <= b->keynum;index++)
{
T->key[index + T->keynum] = b->key[index];
T->ptr[index + T->keynum] = b->ptr[index];
T->keynum++;
}
free(b);
for (index = bronum;index <= f->keynum;index++)
{
f->key[index] = f->key[index + ];
f->ptr[index] = f->ptr[index + ];
}
f->keynum--;
}
renewParent(f);
if (f->keynum == (m + ) / - )
{
//调用借兄弟的函数
return borrowBNode(f);
}
}
else//如果兄弟能够帮你
{
if (bronum < mynum) //如果我不是第一个
{
for (index = ;index <= T->keynum;index++)
{
T->key[index + ] = T->key[index];
T->ptr[index + ] = T->ptr[index];
}
T->ptr[] = T->ptr[];
T->key[] = f->key[mynum];
T->ptr[] = b->ptr[b->keynum];
T->keynum++;
f->key[mynum] = b->key[b->keynum];
b->key[b->keynum] = ;
b->ptr[b->keynum] = NULL;
b->keynum--; }
else //如果我是第一个
{
T->keynum++;
T->key[T->keynum] = f->key[];
T->ptr[T->keynum] = b->ptr[];
f->key[] = b->key[];
b->ptr[] = b->ptr[];
for (index = ;index <= b->keynum;index++)
{
b->key[index] = b->key[index + ];
b->ptr[index] = b->ptr[index + ];
}
b->keynum--;
}
}
return OK;
}
遍历，输出：
为了让B树更容易看，代码更容易调试，我同时还用队列写了个层次遍历，这个看看就好，实现起来挺麻烦的。而且可能代码实现也存在问题
/***
* @name Status ergodic(BTree T, LinkList L, int newline, int sum)
* @description print需要用到的递归遍历程序
* @return 成功返回OK
* @notice 此处用到队列
***/
Status ergodic(BTree T, LinkList L, int newline, int sum)
{
int index;
BTree p;
if (T != NULL)
{
printf("[ ");
Enqueue_L(L, T->ptr[]);
for (index = ;index <= T->keynum; index++)
{
printf("%d ", T->key[index]);
Enqueue_L(L, T->ptr[index]);
}
sum += T->keynum + ;
printf("]");
if (newline == )
{
printf("\n");
newline = sum - ;
sum = ;
}
else
{
--newline;
}
}
if (IfEmpty(L) == FALSE)
{
Dequeue_L(L, p);
ergodic(p, L, newline, sum);
}
return OK;
}
/***
* @name Status print(BTree T)
* @description 层次遍历并分层输出B树
* @return 成功返回OK
* @notice
***/
Status print(BTree T)
{
LinkList L;
if (T == NULL)
{
printf("[ ]\n");
return OK;
}
InitQueue_L(L);
ergodic(T, L, , );
DestroyQueue(L);
return OK;
}
3.测试
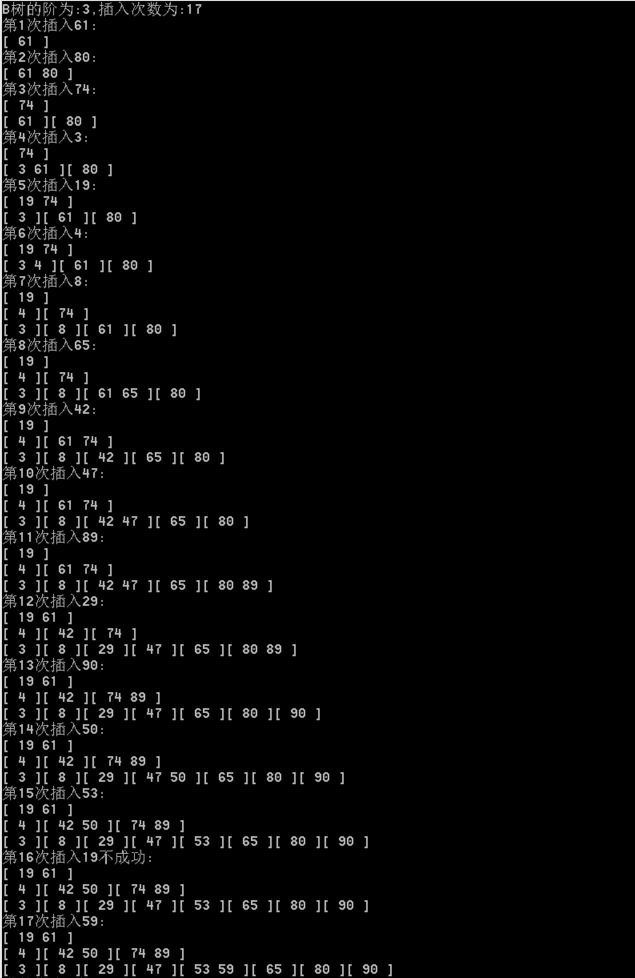
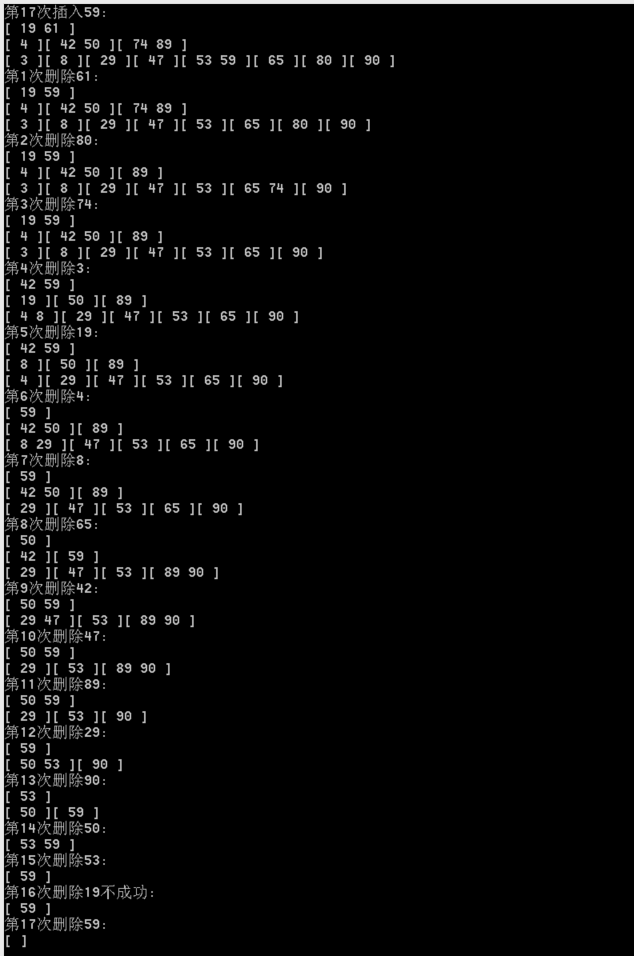
4.总结
以目前所掌握的知识，终于把B树做出来了，整个过程没有参考过其他人的代码，所以并不知道自己的一些思路是否得当，如有错误，多多包涵。在整个过程中，最难，卡的最久的也就是合并操作了，这块的代码也是乱得掉渣，以后有时间把他完善了。最后附上完整代码。
#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
#include<stdlib.h>
#include<time.h>
#define BTREELENGTH 50
#define BTLEN (sizeof(BTNode))
#define MAXINT 100
typedef enum status
{
TRUE,
FALSE,
OK,
ERROR,
OVERFLOW,
EMPTY
}Status;
typedef int KeyType; //**********************************B树****************************************
#define m 3 // B树的阶，此设为4
typedef struct
{
KeyType key;
char data;
} Record;
typedef struct BTNode
{
int keynum; // 结点中关键字个数，即结点的大小
struct BTNode *parent; // 指向双亲结点
KeyType key[m + ]; // 关键字向量，0号单元未用
struct BTNode *ptr[m + ]; // 子树指针向量
// Record *recptr[m + 1]; // 记录指针向量，0号单元未用
//在此添加其他自定义数据
} BTNode, *BTree; // B树结点和B树的类型
typedef struct
{
BTNode *pt; // 指向找到的结点
int i; // 1..m，在结点中的关键字序号
int tag; // 1:查找成功，0:查找失败
} Result; // 在B树的查找结果类型
//**********************************B树**************************************** //**********************************队列***************************************
typedef struct LNode {
BTree data; // 数据域
struct LNode *next; // 指针域
} LNode, *LinkList;
//**********************************队列*************************************** /***
* @name Status InitQueue_L(LinkList &L)
* @description 初始化队列
* @return 成功返回OK，开辟空间失败返回OVERFLOW
* @notice
***/
Status InitQueue_L(LinkList &L)
{ // 初始化一个只含头结点的空单链表L
if (NULL == (L = (LNode*)malloc(sizeof(LNode)))) // 生成新结点
return OVERFLOW;
L->next = NULL;
return OK;
}
/***
* @name LNode* MakeNode_L(BTree e)
* @description 构造队列结点
* @return 返回结点地址
* @notice
***/
LNode* MakeNode_L(BTree e)
{ // 构造数据域为e的单链表结点
LNode *p;
p = (LNode*)malloc(sizeof(LNode)); // 分配结点空间
if (p != NULL)
{
p->data = e;
p->next = NULL;
}
return p;
}
/***
* @name Status Enqueue_L(LNode *p, BTree e)
* @description 队列的入队
* @return 成功返回OK，否则返回ERROR
* @notice
***/
Status Enqueue_L(LNode *p, BTree e)
{ //在p结点之后插入q结点
if (NULL == p) return ERROR; // 参数不合理
while (p->next != NULL)
p = p->next;
p->next = MakeNode_L(e); // 对应图4.11（b）的②，修改p结点的指针域
return OK;
} /***
* @name Status Dequeue_L(LNode *p, BTree &e)
* @description 队列的出队
* @return 成功返回OK，否则返回ERROR
* @notice
***/
Status Dequeue_L(LNode *p, BTree &e)
{
// 删除p结点的直接后继结点并用参数e返回被删结点的值
LNode *q;
if (NULL == p || NULL == p->next) return ERROR; // 删除位置不合理
q = p->next;
p->next = q->next; // 修改被删结点q的指针域
e = q->data;
free(q); // 释放结点q
return OK;
} /***
* @name void DestroyQueue(LinkList L)
* @description 队列的销毁
* @return 无返回
* @notice
***/
void DestroyQueue(LinkList L)
{
// 销毁整个链表
LinkList p;
if (L != NULL)
{
p = L;
L = L->next;
free(p);
DestroyQueue(L);
}
}
/***
* @name Status IfEmpty(LinkList L)
* @description 判断队列是否为空
* @return 空返回TRUE，不空返回FALSE，否则返回ERROR
* @notice
***/
Status IfEmpty(LinkList L)
{
if (L == NULL) return ERROR;
if (L->next == NULL) return TRUE;
return FALSE;
}
/***
* @name Status ergodic(BTree T, LinkList L, int newline, int sum)
* @description print需要用到的递归遍历程序
* @return 成功返回OK
* @notice 此处用到队列
***/
Status ergodic(BTree T, LinkList L, int newline, int sum)
{
int index;
BTree p;
if (T != NULL)
{
printf("[ ");
Enqueue_L(L, T->ptr[]);
for (index = ;index <= T->keynum; index++)
{
printf("%d ", T->key[index]);
Enqueue_L(L, T->ptr[index]);
}
sum += T->keynum + ;
printf("]");
if (newline == )
{
printf("\n");
newline = sum - ;
sum = ;
}
else
{
--newline;
}
}
if (IfEmpty(L) == FALSE)
{
Dequeue_L(L, p);
ergodic(p, L, newline, sum);
}
return OK;
}
/***
* @name Status print(BTree T)
* @description 层次遍历并分层输出B树
* @return 成功返回OK
* @notice
***/
Status print(BTree T)
{
LinkList L;
if (T == NULL)
{
printf("[ ]\n");
return OK;
}
InitQueue_L(L);
ergodic(T, L, , );
DestroyQueue(L);
return OK;
} /***
* @name Status findMax(BTree T, BTree &p,int ans)
* @description 寻找最大关键字的结点,T为要寻找的树，p为返回的节点,ans为第几个
* @return 成功返回OK,否则返回ERROR
* @notice
***/
Status findMax(BTree T, BTree &p, int &ans)
{
if (T == NULL)
return ERROR;
p = T;
while (p->ptr[p->keynum] != NULL)
{
p = p->ptr[p->keynum];
}
ans = p->keynum;
return OK;
}
/***
* @name Status findMin(BTree T, BTree &p,int ans)
* @description 寻找最小关键字的结点,T为要寻找的树，p为返回的节点,ans为第几个
* @return 成功返回OK,否则返回ERROR
* @notice
***/
/***
* @name Status findBTree(BTree T, BTree &p, int &ans, KeyType k)
* @description 寻找 ,T为要寻找的树，p为返回的节点，ans为第几个元素，k为要找的值
* @return 成功返回OK,否则返回ERROR
* @notice
***/
Status findBTree(BTree T, BTree &p, int &ans, KeyType k)
{
BTree q;
int index = ;
KeyType keynow;
if (T == NULL)
return ERROR;
q = T;
keynow = T->key[];
while (q != NULL) //深度的遍历
{
index = ;
keynow = q->key[index];
while (index <= q->keynum) //节点内对各真值进行遍历
{
if (k == keynow) //找到元素
{
p = q;
ans = index;
return TRUE;
}
if (k > keynow)
{
if (index == q->keynum)
{
if (q->ptr[index] == NULL)
{
p = q;
ans = q->keynum + ;
return FALSE;
}
q = q->ptr[index];
break;
}
++index;
keynow = q->key[index];
continue;
}
if (k < keynow)
{
if (q->ptr[index - ] == NULL)
{
p = q;
ans = index;
return FALSE;
}
q = q->ptr[index - ];
break;
}
}
} return ERROR;
}
/***
* @name Status renewParent(BTree p)
* @description 告诉孩子们亲身爸爸是谁
* @return 成功返回OK,否则返回ERROR
* @notice
***/
Status renewParent(BTree p)
{
int index;
if (p == NULL) return ERROR;
for (index = ;index <= p->keynum;++index)
{
if (p->ptr[index] != NULL)
{
p->ptr[index]->parent = p;
renewParent(p->ptr[index]);
}
}
return OK;
}
/***
* @name int whichSon(BTree T)
* @description 找出是父亲的第几个孩子
* @return 成功返回第几个孩子,否则返回-1
* @notice
***/
int whichSon(BTree T)
{
int index = -;
if (T == NULL) return -;
for (index = ;index <= T->parent->keynum;++index) //找出是父亲的第几个孩子
{
if (T->parent->ptr[index] == T) return index;
}
return -;
}
/***
* @name status splitBTree(BTree T)
* @description 递归实现分裂节点操作
* @return 成功返回OK,否则返回ERROR
* @notice
***/
Status splitBTree(BTree T) //此时分裂的节点一定会是超出最大值的。
{
BTree t1, t2;
int index, index_1;
if (T->parent == NULL)
{
t1 = (BTree)malloc(BTLEN);
if (NULL == t1) return OVERFLOW;
t2 = (BTree)malloc(BTLEN);
if (NULL == t2) return OVERFLOW; t1->keynum = m / ;
t2->keynum = m - (m / ) - ;
t1->parent = T;
t2->parent = T;
for (index = ;index <= m; ++index) //先全部初始化
{
t1->ptr[index] = NULL;
t1->key[index] = ;
t2->ptr[index] = NULL;
t2->key[index] = ;
}
for (index = ;index <= m / ; ++index) //初始化t1
{
t1->ptr[index] = T->ptr[index];
t1->key[index] = T->key[index];
}
t2->ptr[] = T->ptr[(m / ) + ];
for (index = (m / ) + ;index <= m; ++index) //初始化t2
{
t2->ptr[index - ((m / ) + )] = T->ptr[index];
t2->key[index - ((m / ) + )] = T->key[index];
}
T->keynum = ;
T->ptr[] = t1;
T->ptr[] = t2;
T->key[] = T->key[m / + ];
for (index = ;index <= m; ++index) //初始化T
{
T->ptr[index] = NULL;
T->key[index] = ;
}
return OK;
} index = whichSon(T);
for (index_1 = T->parent->keynum;index_1 > index;--index_1) //腾出父亲的位置
{
T->parent->ptr[index_1 + ] = T->parent->ptr[index_1];
T->parent->key[index_1 + ] = T->parent->key[index_1];
}
T->parent->keynum++;
T->parent->key[index + ] = T->key[m / + ];
t2 = T->parent->ptr[index + ] = (BTree)malloc(BTLEN);
if (NULL == t2) return OVERFLOW;
for (index = ;index <= m; ++index) //先全部初始化
{
t2->ptr[index] = NULL;
t2->key[index] = ;
}
t2->keynum = m - (m / ) - ;
t2->parent = T->parent;
t2->ptr[] = T->ptr[(m / ) + ];
for (index = (m / ) + ;index <= m; ++index) //初始化t2
{
t2->ptr[index - ((m / ) + )] = T->ptr[index];
t2->key[index - ((m / ) + )] = T->key[index];
}
T->keynum = m / ;
for (index = (m / ) + ;index <= m; ++index) //初始化t2
{
T->ptr[index] = NULL;
T->key[index] = ;
}
if (T->parent->keynum == m)
{
splitBTree(T->parent);
}
return OK;
}
/***
* @name Status insertBTree(BTree &T, Record e)
* @description 插入实现元素的插入
* @return 成功返回OK,如果存在则返回FALSE，否则返回ERROR
* @notice
***/
Status insertBTree(BTree &T, Record e)
{
BTree p;
int index, temp;
Status find_flag;
if (NULL == T)
{
T = (BTree)malloc(BTLEN);
if (NULL == T) return OVERFLOW;
T->keynum = ;
T->parent = NULL;
for (index = ;index <= m; ++index)
{
T->ptr[index] = NULL;
T->key[index] = ;
}
T->key[] = e.key;
return OK;
}
find_flag = findBTree(T, p, temp, e.key);
if (find_flag == TRUE)
{
return FALSE;
}
if (find_flag == FALSE)
{ //不管怎样先直接插入
p->keynum++;
for (index = p->keynum;index > temp;--index)
{
p->key[index] = p->key[index - ];
p->ptr[index] = p->ptr[index - ];
}
p->ptr[temp] = NULL;
p->key[temp] = e.key;
if (p->keynum == m) //这种情况得分裂
{
splitBTree(p);
}
renewParent(T);
return OK;
}
return ERROR;
}
/***
* @name Status borrowBNode(BTree &T)
* @description 递归实现，向兄弟借元素，否则和兄弟合并
* @return 成功返回OK,否则返回ERROR
* @notice 这种情况应该是T为单元素结点
***/
Status borrowBNode(BTree T)
{
int mynum, bronum, index;
BTree b = NULL, f = NULL;
if (T == NULL) return ERROR;
f = T->parent;
if (f == NULL)//考虑父亲结点不存在的情况
{
if (T->keynum == )
{
f = T->ptr[];
if (f == NULL)
{
free(T);
return EMPTY;
}
for (index = ;index <= f->keynum;index++)
{
T->key[index] = f->key[index];
T->ptr[index] = f->ptr[index];
}
T->keynum = f->keynum;
free(f);
renewParent(T);
}
return OK;
}
mynum = whichSon(T);
if (mynum == )
bronum = ;
else
bronum = mynum - ;
b = f->ptr[bronum];
if (b->keynum == (m + ) / - ) //如果兄弟帮不了你了
{
//那么就和这个兄弟合体
if (bronum < mynum) //如果我不是第一个
{
b->keynum++;
b->key[b->keynum] = f->key[mynum];
b->ptr[b->keynum] = T->ptr[];
for (index = ;index <= T->keynum;index++)
{
b->key[index + b->keynum] = T->key[index];
b->ptr[index + b->keynum] = T->ptr[index];
b->keynum++;
}
free(T);
for (index = mynum;index <= f->keynum;index++)
{
f->key[index] = f->key[index + ];
f->ptr[index] = f->ptr[index + ];
}
f->keynum--;
}
else
{
T->keynum++;
T->key[T->keynum] = f->key[bronum];
T->ptr[T->keynum] = b->ptr[];
for (index = ;index <= b->keynum;index++)
{
T->key[index + T->keynum] = b->key[index];
T->ptr[index + T->keynum] = b->ptr[index];
T->keynum++;
}
free(b);
for (index = bronum;index <= f->keynum;index++)
{
f->key[index] = f->key[index + ];
f->ptr[index] = f->ptr[index + ];
}
f->keynum--;
}
renewParent(f);
if (f->keynum == (m + ) / - )
{
//调用借兄弟的函数
return borrowBNode(f);
}
}
else//如果兄弟能够帮你
{
if (bronum < mynum) //如果我不是第一个
{
for (index = ;index <= T->keynum;index++)
{
T->key[index + ] = T->key[index];
T->ptr[index + ] = T->ptr[index];
}
T->ptr[] = T->ptr[];
T->key[] = f->key[mynum];
T->ptr[] = b->ptr[b->keynum];
T->keynum++;
f->key[mynum] = b->key[b->keynum];
b->key[b->keynum] = ;
b->ptr[b->keynum] = NULL;
b->keynum--; }
else //如果我是第一个
{
T->keynum++;
T->key[T->keynum] = f->key[];
T->ptr[T->keynum] = b->ptr[];
f->key[] = b->key[];
b->ptr[] = b->ptr[];
for (index = ;index <= b->keynum;index++)
{
b->key[index] = b->key[index + ];
b->ptr[index] = b->ptr[index + ];
}
b->keynum--;
}
}
return OK;
} /***
* @name Status deleteBTreeRecord(BTree &T, Record e)
* @description 实现B树元素的删除
* @return 成功返回OK,否则返回ERROR
* @notice
***/
Status deleteBTreeRecord(BTree &T, Record e)
{
BTree p, q;
int num, temp, index;
Status find_flag;
if (T == NULL)
return ERROR;
find_flag = findBTree(T, p, temp, e.key);
if (find_flag == FALSE)
{
return FALSE;
}
if (find_flag == TRUE)
{
//deleteBTreeBNode(p,temp);
if (p->ptr[temp] == NULL) //如果是叶子节点的话
{
for (index = temp;index <= p->keynum;++index)
{
p->key[index] = p->key[index + ];
p->ptr[index] = p->ptr[index + ];
}
p->keynum--;
if (p->keynum == (m + ) / - )
{
//调用借兄弟的函数
if (borrowBNode(p) == EMPTY) T = NULL;
else renewParent(T);
}
return OK;
}
else //不是叶子结点的话
{
//遍历
findMax(p->ptr[temp - ], q, num);//返回的q一定会是叶子节点
p->key[temp] = q->key[num];
q->key[num] = ;
q->keynum--;
if (q->keynum == (m + ) / - )
{
//调用借兄弟的函数
if (borrowBNode(q) == EMPTY) T = NULL;
else renewParent(T);
}
return OK;
}
return OK;
}
return ERROR;
}
/***
* @name Status initBTree(BTree &t)
* @description 初始化一个空B树
* @return 成功返回OK
* @notice
***/
Status initBTree(BTree &t)
{
t = NULL;
return OK;
}
/***
* @name Status test()
* @description 针对数据结构实验做的测试函数
* @return 成功返回OK
* @notice
***/
Status test()
{
// 测试代码
int n, i;
int arr[BTREELENGTH];
BTree a;
Record d;
srand((unsigned)time(NULL));
n = rand() % BTREELENGTH;
//scanf("%d", &n); //可以改为自己输入数据
printf("B树的阶为:%d,插入次数为:%d\n", m, n);
initBTree(a);
for (i = ;i < n;i++)
{
d.key = rand() % MAXINT;
//scanf("%d", &d.key); //可以改为自己输入数据
arr[i] = d.key;
if (insertBTree(a, d) == OK)
printf("第%d次插入%d:\n", i + , d.key);
else
printf("第%d次插入%d不成功:\n", i + , d.key);
print(a);
}
for (i = ;i < n;i++)
{
d.key = arr[i];
if (deleteBTreeRecord(a, d) == OK)
printf("第%d次删除%d:\n", i + , d.key);
else
printf("第%d次删除%d不成功:\n", i + , d.key);
print(a);
}
return OK; }
/***
主函数
***/
int main()
{
test();
return ;
}
BTree
B树——思路、及C语言代码的实现的更多相关文章
- 机器学习十大算法总览（含Python3.X和R语言代码）
引言 一监督学习 二无监督学习 三强化学习 四通用机器学习算法列表 线性回归Linear Regression 逻辑回归Logistic Regression 决策树Decision Tree 支持向 ...
- c语言代码规范
什么叫规范?在C语言中不遵守编译器的规定,编译器在编译时就会报错,这个规定叫作规则.但是有一种规定,它是一种人为的.约定成俗的,即使不按照那种规定也不会出错,这种规定就叫作规范.虽然我们不按照规范也不 ...
- Latex中插入C语言代码
Latex是一个文本排版的语言,能排版出各种我们想要的效果.而且用代码排版的优点是易于修改板式,因此在文本内容的排版时,Latex应用十分广泛. 当我们需要在Latex中插入代码时,就需要用到 \us ...
- loadrnner添加C语言代码的几种方式
今天有人在群里问,想直接把自己的C语言代码让lr调用,该怎么搞. 这东西说来简单,只是对Loadrunner这工具不熟悉可能才会有这种问题吧.个人理解,一般有三种方法吧,废话不多,直接干货. 1.直接 ...
- HTML之一语言代码
HTML的lang属性可用于网页或部分网页的语言.这对搜索引擎和浏览器是有帮助的. 同时也可以是指HTTP Header中的Accept-Language/Content-Language. ISO ...
- 让你的Windows不断重启的C语言代码
原文:让你的Windows不断重启的C语言代码 没有写Linux的原因是因为搞不定Linux下的权限问题,而Windows下基本上使用电脑的用户都是管理员,所以钻个空了,不多说下面是代码#includ ...
- 国家语言，语言代码，locale id对应表
国家语言,语言代码,locale id对应表.比如 en_US对应的id为1033, 中文的locale=zh_CN,id=2052. Locale Languagecode LCIDstring L ...
- 如何提高单片机C语言代码效率
代码效率包括两个方面内容:代码的大小和代码执行速度.如果代码精简和执行速度快,我们就说这个代码效率高.一般情况下,代码精简了速度也相应提上来了.单片机的ROM和RAM的空间都很有限,当您编程时遇到单片 ...
- 使用highlight.js高亮静态页面的语言代码
显示静态的代码其实html的pre标签基本可以满足需求了,至少不会将换行的文本显示成一堆字符串. 不过能使静态的文本能高亮显示,倒更炫酷一点.其实很简单的,引入highlight.js包,可以使用cd ...
随机推荐
- C#时间戳的获取与转换方法
/// <summary> /// 获取当前时间戳 /// </summary> /// <param name="bflag"></pa ...
- 【网络流#7】POJ 3281 Dining 最大流 - 《挑战程序设计竞赛》例题
不使用二分图匹配,使用最大流即可,设源点S与汇点T,S->食物->牛->牛->饮料->T,每条边流量为1,因为流过牛的最大流量是1,所以将牛拆成两个点. 前向星,Dini ...
- 综合使用LruCache和DiskLruCache 缓存图片
Activity public class MainActivity extends Activity { private GridView mPhotoWall; private P ...
- Java多线程——线程池
系统启动一个新线程的成本是比较高的,因为它涉及到与操作系统的交互.在这种情况下,使用线程池可以很好的提供性能,尤其是当程序中需要创建大量生存期很短暂的线程时,更应该考虑使用线程池. 与数据库连接池类似 ...
- Jquery+css实现图片无缝滚动轮播
Today,在XX学院的教学视频中,偶尔看到了Jquery+css实现图片无缝滚动轮播视频教程,虽然以前已写过类似的,但是我感觉他学的比较精简.为了方便以后做项目时直接拷贝,特地写出来,顺便和大家分享 ...
- 学习日记-----ORM
ORM ORM(Object Relation Mapping)对象关系映射 实质:将数据库中 的业务数据用对象的形式表现出来,使用ORM在业务逻辑层和数据访问层之间充当桥梁 核心原则: 简单性 传达 ...
- WinAPI——谐振动的合成
#include<Windows.h> #include<math.h> #define NUM 1000 #define PI 3.14159 LRESULT CALLBAC ...
- Nginx配置域名跳转实例
要求:浏览器地址栏输入qj.123.com之后,地址自动变成qj.abc.com 配置nginx跳转 server { listen 80; server_name qj.abc.com qj.123 ...
- iOS UI_APPEARANCE_SELECTOR
iOS后属性带UI_APPEARANCE_SELECTOR 可以统一设置全局作用 例如: 1>开关控件 @property(nullable, nonatomic, strong) UIColo ...
- 设置Activity显示和关闭时的动画效果
设置Activity显示和关闭时的动画效果 通过overridePendingTransition方法可以设置Activity显示和关闭的动画效果.首先需要在res/anim目录中建立相应的动画资源文 ...