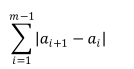被sjy带刷题#1
笔记
【问题描述】
给定一个长度为m的序列a,下标编号为1~m。序列的每个元素都是1~n的
整数。定义序列的代价为你现在可以选择两个数x和y,并将序列a中所有的x改成y。x可以与y相等。
请求出序列最小可能的代价。
【输入格式】
输入第一行包含两个整数n和m。第二行包含m个空格分隔的整数,代表序
列a。
【输出格式】
输出一行,包含一个整数,代表序列最小的代价。
【样例输入 1】
4 6
1 2 3 4 3 2
【样例输出 1】
3
【样例输入 2】
10 5
9 4 3 8 8
【样例输出 1】
6
【样例解释】
样例 1 中,最优策略为将 4 改成 3。样例 2 中,最优策略为将 9 改成 4。
【数据规模和约定】对于30%的数据,n,m<=100.
对于60%的数据,n,m ≤ 2000。
对于100%的数据,1 ≤ n,m≤ 100,000。
城堡
【问题描述】
给定一张N个点M条边的无向连通图,每条边有边权。我们需要从M条边中
选出N − 1条, 构成一棵树。 记原图中从 1 号点到每个节点的最短路径长度为Di ,
树中从 1 号点到每个节点的最短路径长度为? ? ,构出的树应当满足对于任意节点
i,都有Di = Si 。
请你求出选出N − 1条边的方案数。
【输入格式】
输入的第一行包含两个整数N和M。
接下来M行,每行包含三个整数u、v和w,描述一条连接节点u和v且边权为
w的边。
【输出格式】
输出一行,包含一个整数,代表方案数对2^31 − 1取模得到的结果。
【样例输入】
3 3
1 2 2
1 3 1
2 3 1
【样例输出】
2
【数据规模和约定】
对于20%的数据,2<=N<=5,M<=10.
对于50%的数据,满足条件的方案数不超过 10000。
对于100%的数据,2≤ N ≤ 1000,N-1 ≤ M ≤ N(N-1)/2,1<=w<=100.
#include <iostream>
#include <cstdio>
#include <cstring>
#include <queue>
#define maxn 1000
#define maxm 500000
#define mod 1<<31-1
using namespace std;
typedef long long LL;
int m,n;
int w[maxn][maxn], s[maxn][maxn], num[maxn], d[maxn];
LL dis[maxn], sum[maxn], ans();
queue<int> que;
int main(){
ios::sync_with_stdio(false);
cin >> n >> m;
for (int i=;i<=m;i++) {
int u,v,value;cin>>u>>v>>value;
w[u][v] = w[v][u] = value;
s[u][++num[u]] = v;
s[v][++num[v]] = u;
}
for (int i=;i<=n;i++) dis[i] = 0x7fffff;
que.push();d[] = ;dis[] = ;
do{
int h = que.front();d[h] = ;
que.pop();
for (int i=;i<=num[h];i++){
if (dis[s[h][i]] > dis[h] + w[h][s[h][i]]){
dis[s[h][i]] = dis[h] + w[h][s[h][i]];
if (!d[s[h][i]]){
que.push(s[h][i]),d[s[h][i]] = ;
}
}
}
}while(!que.empty());
que = queue<int>();
memset(d, , sizeof(d));
que.push(),d[] = ,sum[] = ;
do{
int h = que.front();d[h] = ;
que.pop();
for (int i=;i<=num[h];i++){
if (dis[s[h][i]] == dis[h]+w[h][s[h][i]]){
sum[s[h][i]] == mod ? sum[s[h][i]] = : sum[s[h][i]]++;
if (!d[s[h][i]]) {
que.push(s[h][i]),d[s[h][i]] = ;
}
}
}
}while(!que.empty());
for (int i=;i<=n;i++) ans=(ans*sum[i])%m;
cout << ans << endl;
return ;
}
castle.cpp
被sjy带刷题#1的更多相关文章
- LeetCode刷题系列
LeetCode 我们工作面试和提高自身数据结构和算法能力的时候往往需要刷刷题,我选择LeetCode是通过一个留学论坛了解的.专业,覆盖语种全面. 提前说说刷题的心得: 尽量手写代码,少使用IDE的 ...
- python部落刷题宝学到的内置函数(二)
感觉到刷题宝有一个好处,也许也不是好处,它的答案必须是真正输出的值,也就是说应该输出字符串aaaa的时候,答案必须写成界面上返回的值,即'aaaa'.有利于真正记忆返回值类型,但是....太繁琐了 1 ...
- [刷题]算法竞赛入门经典(第2版) 4-6/UVa508 - Morse Mismatches
书上具体所有题目:http://pan.baidu.com/s/1hssH0KO 代码:(Accepted,10 ms) //UVa508 - Morse Mismatches #include< ...
- NOIp2018停课刷题记录
Preface 老叶说了高中停课但是初中不停的消息后我就为争取民主献出一份力量 其实就是和老师申请了下让我们HW的三个人听课结果真停了 那么还是珍惜这次机会好好提升下自己吧不然就\(AFO\)了 Li ...
- 周刷题第一期总结(two sum and two numbers)
由于深深的知道自己是事件驱动型的人,一直想补强自己的薄弱环节算法,却完全不知道从哪里入手.所以只能采用最笨的办法,刷题.从刷题中遇到问题就解决问题,最后可能多多少少也能提高一下自己的渣算法吧. 暂时的 ...
- 湾区求职分享:三个月刷题拿到 Google offer,欢迎踊跃提问
本文仅以个人经历和个人观点作为参考.如能受益,不胜荣幸. 本文会不断的修正,更新.希望通过大家的互动最后能写出一份阅者受益的文章. 本文纯手打,会有错别字,欢迎指出,虚心接受及时更改. 小马过河,大牛 ...
- 牛客网Java刷题知识点之Java 集合框架的构成、集合框架中的迭代器Iterator、集合框架中的集合接口Collection(List和Set)、集合框架中的Map集合
不多说,直接上干货! 集合框架中包含了大量集合接口.这些接口的实现类和操作它们的算法. 集合容器因为内部的数据结构不同,有多种具体容器. 不断的向上抽取,就形成了集合框架. Map是一次添加一对元素. ...
- 牛客网Java刷题知识点之泛型概念的提出、什么是泛型、泛型在集合中的应用、泛型类、泛型方法、泛型接口、泛型限定上限、泛型限定下限、 什么时候使用上限?泛型限定通配符的体现
不多说,直接上干货! 先来看个泛型概念提出的背景的例子. GenericDemo.java package zhouls.bigdata.DataFeatureSelection; import ja ...
- noip2019——动态规划刷题历程
加粗的是值得总结的 从洛谷的普及题开始刷题: 背包式dp(有些技巧的) 1.p2639[USACO09OCT]Bessie的体重问题 -p1049取模意义下01背包 技巧:重量=价值 2.金明的预算问 ...
随机推荐
- 初学QML之qmlRegisterType
qmlRegisterType 是一个可以将C++实现的类在QML中调用的,连接C++和QML的一个工具 首先来看QtAssistant的介绍 int qmlRegisterType(const ch ...
- html中embed标签的用法
(一).基本语法: embed src=url 说明:embed可以用来插入各种多媒体,格式可以是 Midi.Wav.AIFF.AU.MP3等等,Netscape及新版的IE 都支持.url为音频或视 ...
- 使用ARM模板在Azure中国大规模部署DCOS集群
容器技术是目前非常流行的技术,尤其是在以Docker作为容器引擎的推动下,让容器的轻量级,可移植,自包含,隔离性等的上了一个新的台阶,目前谈及Dev/Ops,CI/CD很少能够绕过Docker的. A ...
- FPGA技术的一些基本概念(综合、BlackBox)(转)
原文:http://blog.sina.com.cn/s/blog_6254a8ca0100i0wr.html 原文也是转的,哈哈,大家多转转,转转更健康.删除了一些Xilinx的东西 前言 综合是将 ...
- Android中focusable属性的妙用——底层按钮的实现
http://www.cnblogs.com/kofi1122/archive/2011/03/22/1991828.html http://www.juziku.com/weizhishi/3077 ...
- 《Programming WPF》翻译 第6章 1.创建和使用资源
原文:<Programming WPF>翻译 第6章 1.创建和使用资源 资源这个词具有非常广泛的意义.任何对象都可以是一个资源.一个在用户界面中经常使用的Brush或者Color可以是一 ...
- 无人参与安装IIS 6.0
使用脚本安装 IIS 从“开始”菜单,单击“运行”. 在“打开”框中,键入 cmd,然后单击“确定”. 在命令提示符下,键入 Sysocmgr.exe /i:sysoc.inf /u:%path_to ...
- java查找重复类/jar包/普通文件
开发web应用时,有时更新了类却没有生效,其实是因为jboss/tomcat中其他发布包下有同名类(包括全路径都相同). 于是萌发了做个程序来检查指定目录是否存在重复类(通过asm从类文件中取类的全路 ...
- unix c 08
信号 - signal()改变信号的处理方式.默认情况下,信号在Unix中都有自己的处理方式,如果想改变信号的处理方式,signal/sigaction 可以实现. 信号可以在关键代码处进行屏蔽,因为 ...
- 瑞柏匡丞:app商业价值如何体现
在互联网行业,想要实现商业价值,必须先实现用户价值.这个观点发源自PC统治互联网的时代,如今PC端的用户停留时间下降,用户行为趋于稳定保守,移动端则蒸蒸日上.而PC与移动端的区别之一是,PC端的用户流 ...