lucene评分推导公式

在进行Lucene的搜索过程解析之前，有必要单独的一张把Lucene score公式的推导，各部分的意义阐述一下。因为Lucene的搜索过程，很重要的一个步骤就是逐步的计算各部分的分数。

Lucene的打分公式非常复杂，如下：

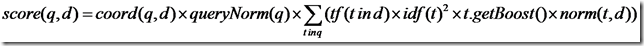
在推导之前，先逐个介绍每部分的意义：

t：Term，这里的Term是指包含域信息的Term，也即title:hello和content:hello是不同的Term 
coord(q,d)：一次搜索可能包含多个搜索词，而一篇文档中也可能包含多个搜索词，此项表示，当一篇文档中包含的搜索词越多，则此文档则打分越高。 
queryNorm(q)：计算每个查询条目的方差和，此值并不影响排序，而仅仅使得不同的query之间的分数可以比较。其公式如下：

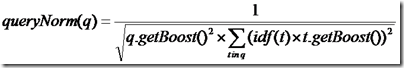
tf(t in d)：Term t在文档d中出现的词频 
idf(t)：Term t在几篇文档中出现过 
norm(t, d)：标准化因子，它包括三个参数： 
Document boost：此值越大，说明此文档越重要。 
Field boost：此域越大，说明此域越重要。 
lengthNorm(field) = (1.0 / Math.sqrt(numTerms))：一个域中包含的Term总数越多，也即文档越长，此值越小，文档越短，此值越大。

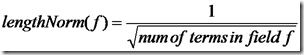
各类Boost值 
t.getBoost()：查询语句中每个词的权重，可以在查询中设定某个词更加重要，common^4 hello 
d.getBoost()：文档权重，在索引阶段写入nrm文件，表明某些文档比其他文档更重要。 
f.getBoost()：域的权重，在索引阶段写入nrm文件，表明某些域比其他的域更重要。 
以上在Lucene的文档中已经详细提到，并在很多文章中也被阐述过，如何调整上面的各部分，以影响文档的打分，请参考有关Lucene的问题(4):影响Lucene对文档打分的四种方式一文。

然而上面各部分为什么要这样计算在一起呢？这么复杂的公式是怎么得出来的呢？下面我们来推导。

首先，将以上各部分代入score(q, d)公式，将得到一个非常复杂的公式，让我们忽略所有的boost，因为这些属于人为的调整，也省略coord，这和公式所要表达的原理无关。得到下面的公式：

然后，有Lucene学习总结之一：全文检索的基本原理中的描述我们知道，Lucene的打分机制是采用向量空间模型的：

我们把文档看作一系列词(Term)，每一个词(Term)都有一个权重(Term weight)，不同的词(Term)根据自己在文档中的权重来影响文档相关性的打分计算。

于是我们把所有此文档中词(term)的权重(term weight) 看作一个向量。

Document = {term1, term2, …… ,term N}

Document Vector = {weight1, weight2, …… ,weight N}

同样我们把查询语句看作一个简单的文档，也用向量来表示。

Query = {term1, term 2, …… , term N}

Query Vector = {weight1, weight2, …… , weight N}

我们把所有搜索出的文档向量及查询向量放到一个N维空间中，每个词(term)是一维。

我们认为两个向量之间的夹角越小，相关性越大。

所以我们计算夹角的余弦值作为相关性的打分，夹角越小，余弦值越大，打分越高，相关性越大。

余弦公式如下：

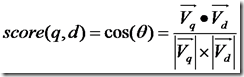
下面我们假设：

查询向量为Vq = <w(t1, q), w(t2, q), ……, w(tn, q)>

文档向量为Vd = <w(t1, d), w(t2, d), ……, w(tn, d)>

向量空间维数为n，是查询语句和文档的并集的长度，当某个Term不在查询语句中出现的时候，w(t, q)为零，当某个Term不在文档中出现的时候，w(t, d)为零。

w代表weight，计算公式一般为tf*idf。

我们首先计算余弦公式的分子部分，也即两个向量的点积：

Vq*Vd = w(t1, q)*w(t1, d) + w(t2, q)*w(t2, d) + …… + w(tn ,q)*w(tn, d)

把w的公式代入，则为

Vq*Vd = tf(t1, q)*idf(t1, q)*tf(t1, d)*idf(t1, d) + tf(t2, q)*idf(t2, q)*tf(t2, d)*idf(t2, d) + …… + tf(tn ,q)*idf(tn, q)*tf(tn, d)*idf(tn, d)

在这里有三点需要指出：

由于是点积，则此处的t1, t2, ……, tn只有查询语句和文档的并集有非零值，只在查询语句出现的或只在文档中出现的Term的项的值为零。 
在查询的时候，很少有人会在查询语句中输入同样的词，因而可以假设tf(t, q)都为1 
idf是指Term在多少篇文档中出现过，其中也包括查询语句这篇小文档，因而idf(t, q)和idf(t, d)其实是一样的，是索引中的文档总数加一，当索引中的文档总数足够大的时候，查询语句这篇小文档可以忽略，因而可以假设idf(t, q) = idf(t, d) = idf(t) 
基于上述三点，点积公式为：

Vq*Vd = tf(t1, d) * idf(t1) * idf(t1) + tf(t2, d) * idf(t2) * idf(t2) + …… + tf(tn, d) * idf(tn) * idf(tn)

所以余弦公式变为：

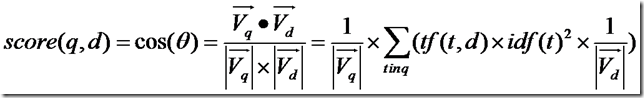
下面要推导的就是查询语句的长度了。

由上面的讨论，查询语句中tf都为1，idf都忽略查询语句这篇小文档，得到如下公式

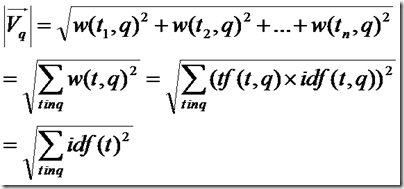
所以余弦公式变为：

下面推导的就是文档的长度了，本来文档长度的公式应该如下：

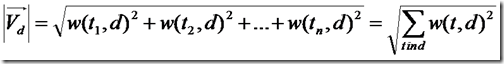
这里需要讨论的是，为什么在打分过程中，需要除以文档的长度呢？

因为在索引中，不同的文档长度不一样，很显然，对于任意一个term，在长的文档中的tf要大的多，因而分数也越高，这样对小的文档不公平，举一个极端的例子，在一篇1000万个词的鸿篇巨著中，"lucene"这个词出现了11次，而在一篇12个词的短小文档中，"lucene"这个词出现了10次，如果不考虑长度在内，当然鸿篇巨著应该分数更高，然而显然这篇小文档才是真正关注"lucene"的。

然而如果按照标准的余弦计算公式，完全消除文档长度的影响，则又对长文档不公平(毕竟它是包含了更多的信息)，偏向于首先返回短小的文档的，这样在实际应用中使得搜索结果很难看。

所以在Lucene中，Similarity的lengthNorm接口是开放出来，用户可以根据自己应用的需要，改写lengthNorm的计算公式。比如我想做一个经济学论文的搜索系统，经过一定时间的调研，发现大多数的经济学论文的长度在8000到10000词，因而lengthNorm的公式应该是一个倒抛物线型的，8000到 10000词的论文分数最高，更短或更长的分数都应该偏低，方能够返回给用户最好的数据。

在默认状况下，Lucene采用DefaultSimilarity，认为在计算文档的向量长度的时候，每个Term的权重就不再考虑在内了，而是全部为一。

而从Term的定义我们可以知道，Term是包含域信息的，也即title:hello和content:hello是不同的Term，也即一个Term只可能在文档中的一个域中出现。

所以文档长度的公式为：

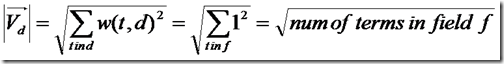
代入余弦公式：

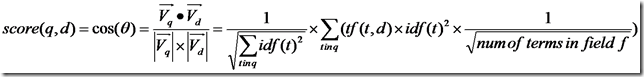
再加上各种boost和coord，则可得出Lucene的打分计算公式。

本文来自CSDN博客，转载请标明出处：http://blog.csdn.net/forfuture1978/archive/2010/03/07/5353126.aspx