AT_abc178_d 题解

洛谷链接&Atcoder 链接

本篇题解为此题较简单做法及较少码量，并且码风优良，请放心阅读。

题目简述

给定一个正整数 \(S\)，问有多少个数满足以下条件：

• 序列中必须为 \(\ge 3\) 的正整数。
• 序列中的和必须为 \(S\)。

思路

首先想到组合数学，本题可通过组合数学插板法解决。

引入：例题，求 \(n\) 个苹果分为 \(k\) 组的方案数，每组苹果个数仅需 \(\ge 1\)。

那么这道题就可转化为：

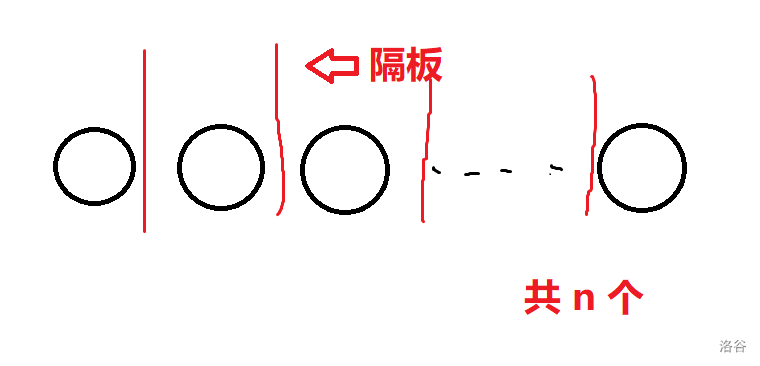
如图，共有 \(n\) 个苹果用 \(k-1\) 个隔板隔开 \(k\) 组，即从 \(n-1\) 个空中选 \(k-1\) 个空插隔板，所以答案即为 \(C_{n-1}^{k-1}\)。

注意：隔板不能重合也不能在两边，因为每组苹果个数需 \(\ge 1\)。

现在再来看此题，发现每组需 \(\ge 3\) 且组数不确定，所以需要枚举组数 \(i\) 从 \(1\) 到 \(n/3\)，并且空格数即可插板的位置数也会发生变化：

\[n-1 \to n-2 \times i-1
\]

隔板数依然不变，是 \(i-1\)。所以对于此题，方案数即为 \(C_{n-2 \times i-1}^{i-1}\)。

接下来就需要解决组合数的计算了，因为此题的数据范围不大，所以就可以用杨辉三角预处理组合数。学过组合数的同学应该都学过，这里直接说结论：杨辉三角的第 \(n\) 行的第 \(i\) 个数即为 \(C_n^i\) 的值。

预处理如下（预处理过程中也要模 \(1000000007\)）：

for(int i = 0; i <= n; i ++) {
		C[i][0] = C[i][j] = 1;
		for(int j = 1; j < i; j ++)
			C[i][j] = (C[i - 1][j - 1] + C[i - 1][j]) % MOD;
	}

经过以上分析及部分代码讲解，基本的代码框架就很清晰了，下面是具体代码实现：

#include<iostream>
using namespace std;
#define MOD 1000000007

int S, C[2005][2005]; // 组合数数组
long long ans = 0; // 记录答案，可不开 long long

int main() {
	cin >> S;
	for(int i = 0; i <= S; i ++) {
		C[i][0] = C[i][j] = 1;
		for(int j = 1; j < i; j ++)
			C[i][j] = (C[i - 1][j - 1] + C[i - 1][j]) % MOD; // 杨辉三角预处理组合数
	}
        // 枚举组数
	for(int i = 1; i <= S / 3; i ++)
		ans = (ans + C[S - 2 * i - 1][i - 1]) % MOD; // 累计答案
        cout << ans << endl; // 输出答案，换行好习惯
	return 0;
}

提交记录：

\[\text{The End!}
\]