[CEOI2011] Matching 题解

前言

题目链接：洛谷。

在上一题之后，模拟赛又放了一道 KMP 重定义相等的问题，但是寄了，故再记之。

题意简述

现在给出 \(1 \sim n\) 的排列 \(p\) 和序列 \(h_1, h_2, \cdots, h_m\)​​，请你求出哪些 \(h\) 的子串符合排列 \(p\)。串 \(a_i\) 符合一个排列被定义为其从小到大排序后得到 \(a_{p_i}\)。

题目分析

先想到定义 \(b_{p_i} = i\)，那么一个串符合 \(p\)，等价于其每个值的排名与 \(b_i\) 相等。

也是考虑，用相对信息来进行匹配。很容易想到，如果对于两个串，每个位置的前驱后继都相等，这两个串是符合上述“符合”的定义的。因为每个数都能够确定在排名中唯一的位置。

由于 KMP 匹配的过程是从左往右扫的过程，我们如果要记相对信息，只能记这个位置和之前位置的相对关系。这是对于 KMP 重定义匹配普遍的结论。这是为什么呢？

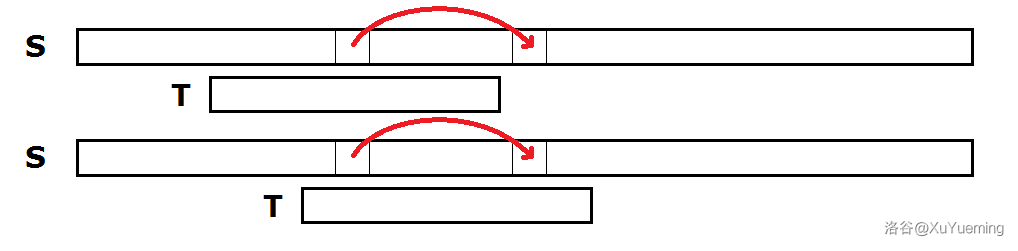
比如，之前我们有一个位置和后面的相对信息超出了当前匹配的范围，我们当做它不存在。但是，随着我们向右扫描的过程中，这个位置可能有被包含了进来，就有可能不符合要求。相反，如果我们记录左边的信息，如果超出范围，就不可能再被包含进来，所以不会出现以上情况。

那我们如何设计新的信息呢？我们假设之前匹配到的位置都暂时符合排名关系，那要新增一个值，让这个值也符合排名位置。这是一个类似于在一个有序的数列里面插入一个值，使得这个值插入的位置满足给出的信息。想到，对于 \(b\) 可以预处理出 \(L_i\) 和 \(R_i\) 分别表示 \(i\) 与在 \(1 \sim i - 1\) 中的前驱后继之差。这也和我们要插进去的位置相关。

所以，假设当前位置为 \(i\)，\(i - 1\) 匹配到的位置为 \(j\)，我们只需要判断 \(S[i - L[j + 1]] < S[i] < S[i + R[j + 1]]\) 就表示可以插到对应位置，满足要求。当然，如果 \(L[j + 1]\) 或 \(R[j + 1]\) 不存在则无需判断。

至于预处理 \(L\) 和 \(R\)，由于 \(b\) 是排列，所以倒序枚举，链表查前驱后继并删去当前数即可。

时间复杂度为 \(\Theta(n + m)\)。

代码

略去了快读快写，是最优解。

// #pragma GCC optimize(3)
// #pragma GCC optimize("Ofast", "inline", "-ffast-math")
// #pragma GCC target("avx", "sse2", "sse3", "sse4", "mmx")
#include <cstdio>
using namespace std;

int n, m;
int xym[1000010], yzh[1000010];
int whr[1000010], fail[1000010];
int L[1000010], R[1000010];
int pre[1000010], nxt[1000010];
int ans[1000010], tot;

inline bool check(int *yzh, int x, int y) {
	return (!L[x] || yzh[y + L[x]] < yzh[y]) && (!R[x] || yzh[y + R[x]] > yzh[y]);
}

signed main() {
	fread(buf, 1, MAX, stdin), read(n), read(m);
	for (int i = 1; i <= n; ++i) {
		read(whr[i]), xym[whr[i]] = i;
		pre[i] = i - 1, nxt[i] = i + 1;
	}
	for (int i = n; i; --i) {
		if (pre[xym[i]]     ) L[i] = whr[pre[xym[i]]] - i;
		if (nxt[xym[i]] <= n) R[i] = whr[nxt[xym[i]]] - i;
		pre[nxt[xym[i]]] = pre[xym[i]];
		nxt[pre[xym[i]]] = nxt[xym[i]];
	}
	for (int i = 1, j = fail[0] = -1; i <= n; ++i) {
		while (~j && !check(xym, j + 1, i)) j = fail[j];
		fail[i] = ++j;
	}
	for (int i = 1; i <= m; ++i) read(yzh[i]);
	for (int i = 1, j = 0; i <= m; ++i) {
		while (~j && (j == n || !check(yzh, j + 1, i))) j = fail[j];
		if (++j == n) ans[++tot] = i - n + 1;
	}
	write(tot), putchar('\n');
	for (int i = 1; i <= tot; ++i) write(ans[i]), putchar(' ');
	fwrite(obuf, 1, o - obuf, stdout);
	return 0;
}