【BZOJ-2669】局部极小值 状压DP + 容斥原理

2669: [cqoi2012]局部极小值

Time Limit: 3 Sec  Memory Limit: 128 MB
Submit: 561  Solved: 293
[Submit][Status][Discuss]

Description

有一个n行m列的整数矩阵，其中1到nm之间的每个整数恰好出现一次。如果一个格子比所有相邻格子（相邻是指有公共边或公共顶点）都小，我们说这个格子是局部极小值。

给出所有局部极小值的位置，你的任务是判断有多少个可能的矩阵。

Input

输入第一行包含两个整数n和m（1<=n<=4, 1<=m<=7），即行数和列数。以下n行每行m个字符，其中“X”表示局部极小值，“.”表示非局部极小值。

Output

输出仅一行，为可能的矩阵总数除以12345678的余数。

Sample Input

3 2
X.
..
.X

Sample Output

60

HINT

Source

Solution

这道题有点劲！自己没想出来，于是看的论文  传送门   下面引用论文里的题解

对于一个合法的数填写方案，其中的数放置的顺序对其是没有影响的，于是我们可以从1开始填数，并且一个一个地填进格子。如果采取这样的做法，那么所有的“X”必然要在其周边所有的格子填数之前就填好一个数，而"X"有多少呢？很显然最多只有8个而已。这时我们就可以想到这样的一个状态压缩方式：opt[i][j]（j是一个二进制表达）表示的是i及其以后的数还没有填进格子，被填写了数的“X”集合状态为j的情况下的方案数。

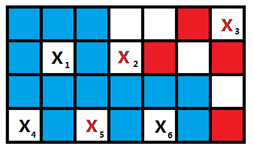
如上图4*7的矩阵中，红色的"X"表示已经填写数的"X"，红色的格子表示已经填写数的非"X"格子，那么可以表述成这样的状态opt[8][num]（8表示已经填写了7个数，下一个填写8，num是011010的表示，含义是第2、3、5个"X"已经填写了数了）

如果我们转移的话就会有两种情况：

第一种情况就是把i填进一个"X"中，这个显然只要枚举一下放哪一个"X"，然后把这个"X"加入j表示的集合里就可以了。

如上图，下一步我们填写"X"是可以随意的，因为只要存在解，任意的"X"都是互不影响的。当前的状态为f[8][num1]（num1为011010的表示），可以推导到f[9][num2](num2为111010、011110、011011的表示)。

第二种情况就是把i填进一个非"X"中，这样的选择就有很多了。对于全图我们一共有n*m个格子，若没有填进去数的"X"格子以及其周边的格子共有tot个，显然这tot个格子都是不能填i的（因为填进的是一个非"X"，并且一个没有填进去数的"X"格子其周边因为都要比它小，所以这两者都不可以填i），又因为已经填写了1到i-1所有的数，所以剩下能填的选择数就是n*m-tot-(i-1)。

如上图，所有的蓝色区域都是无法填写i的，而下一步能填写的格子就只有白色的格子，即4*7-17-7=4个格子。

由于这样的处理方式，尤其是第二种转移可能会导致非"X"点变为最小值，所以还需要使用容斥原理来解决。

Code

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
using namespace std;
#define LL long long
#define P 12345678
int N,M,ANS,bin[],f[][],cnt[];
char mp[][];
int dx[]={-,-,-,,,,,,,},dy[]={-,,,-,,,-,,,};
inline bool OK(int x,int y) {return x>= && x<=N && y>= && y<=M;}
#define Pa pair<int,int>
Pa stack[]; int top;
bool visit[][];
inline void PreWork()
{
    top=;
    for (int i=; i<=N; i++)
        for (int j=; j<=M; j++)
            if (mp[i][j]=='X') stack[top++]=make_pair(i,j);
    for (int i=; i<bin[top]; i++)
        {
            cnt[i]=; memset(visit,,sizeof(visit));
            for (int j=; j<top; j++) if (~i&bin[j]) visit[stack[j].first][stack[j].second]=;
            for (int j=; j<=N; j++)
                for (int k=; k<=M; k++)
                    if (!visit[j][k])
                        {
                            bool flag=;
                            for (int d=,x,y; d<= && flag; d++)
                                x=j+dx[d],y=k+dy[d],flag=!visit[x][y];
                            cnt[i]+=flag;
                        }
        }
}
inline int DP()
{
    PreWork();
    memset(f,,sizeof(f));
    f[][]=;
    for (int i=; i<=N*M; i++)
        for (int j=; j<bin[top]; j++)
            {
                for (int k=; k<top; k++)
                    if (j&bin[k]) (f[i][j]+=f[i-][j^bin[k]])%=P;
                (f[i][j]+=(LL)f[i-][j]*(cnt[j]-(i-))%P)%=P;
            }
    return f[N*M][bin[top]-];
}
inline void DFS(int dep,int x,int y)
{
    if (y==M+) {DFS(dep,x+,); return;}
    if (x==N+) {(ANS+=(LL)DP()*(dep&? -:)%P)%=P; return;}
    DFS(dep,x,y+);
    bool flag=;
    for (int i=; i<= && flag; i++)
        if (mp[x+dx[i]][y+dy[i]]=='X') flag=;
    if (flag) mp[x][y]='X',DFS(dep+,x,y+),mp[x][y]='.';
}
int main()
{
    bin[]=; for (int i=; i<=; i++) bin[i]=bin[i-]<<;
    scanf("%d%d",&N,&M);
    for (int i=; i<=N; i++) scanf("%s",mp[i]+);
    DFS(,,);
    printf("%d\n",(ANS+P)%P);
    return ;
}

菜鸡.jpg