背包DP——完全背包

完全背包模型与 0-1 背包类似，与 0-1 背包的区别仅在于一个物品可以选取无限次，而非仅能选取一次。

而状态转移方程于01背包区别在于可以直接从[i][j-w[i]]转移

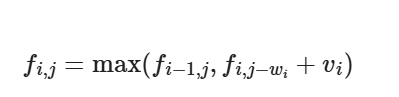
理由是当我们这样转移时，[i][j-w[i]]已经由 [i][j-2*w[i]]更新过，那么 [i][j-w[i]]就是充分考虑了第 i 件物品所选次数后得到的最优结果。

换言之，我们通过局部最优子结构的性质重复使用了之前的枚举过程，优化了枚举的复杂度。

例题

疯狂的采药

题目背景

此题为纪念 LiYuxiang 而生。

题目描述

LiYuxiang 是个天资聪颖的孩子，他的梦想是成为世界上最伟大的医师。为此，他想拜附近最有威望的医师为师。医师为了判断他的资质，给他出了一个难题。医师把他带到一个到处都是草药的山洞里对他说：“孩子，这个山洞里有一些不同种类的草药，采每一种都需要一些时间，每一种也有它自身的价值。我会给你一段时间，在这段时间里，你可以采到一些草药。如果你是一个聪明的孩子，你应该可以让采到的草药的总价值最大。”

如果你是 LiYuxiang，你能完成这个任务吗？

此题和原题的不同点：

\(1\). 每种草药可以无限制地疯狂采摘。

\(2\). 药的种类眼花缭乱，采药时间好长好长啊！师傅等得菊花都谢了！

输入格式

输入第一行有两个整数，分别代表总共能够用来采药的时间 \(t\) 和代表山洞里的草药的数目 \(m\)。

第 \(2\) 到第 \((m + 1)\) 行，每行两个整数，第 \((i + 1)\) 行的整数 \(a_i, b_i\) 分别表示采摘第 \(i\) 种草药的时间和该草药的价值。

输出格式

输出一行，这一行只包含一个整数，表示在规定的时间内，可以采到的草药的最大总价值。

样例 #1

样例输入 #1

70 3
71 100
69 1
1 2

样例输出 #1

140

提示

数据规模与约定

• 对于 \(30\%\) 的数据，保证 \(m \le 10^3\) 。
• 对于 \(100\%\) 的数据，保证 \(1 \leq m \le 10^4\)，\(1 \leq t \leq 10^7\)，且 \(1 \leq m \times t \leq 10^7\)，\(1 \leq a_i, b_i \leq 10^4\)。

Coce

点击查看代码

const int maxn = 1e7 + 10;
int dp[maxn], w[maxn], v[maxn];
void solve() {
    int n, m;
    cin >> m >> n;
    for (int i = 1; i <= n; i++) {
        cin >> w[i] >> v[i];
    }

    for (int i = 1; i <= n; i++) {
        for (int j = w[i]; j <= m; j++) {
            dp[j] = max(dp[j], dp[j - w[i]] + v[i]);
        }
    }

    cout << dp[m];
}