Kulla-Conty BRDF补充_重要性采样GGX

重要性采样的方法有多种，这里我们介绍其中一种，你的实现也可以使用其他方法。我们将通过 GGX 采样来完成 E(µ)的预计算工作。先从理论上讨论 GGX

采样算法，对于给定出射方向 o 的 GGX采样，目标是采样生成入射方向 i 以计算

\(\frac{f r (i,o,h)(i,n)}{pdf i (i)}\)。因此，对于 GGX 算法有两个核心问题需要解决：如何采样和对应的概率 pdf 是什么。

第一个问题，如何采样入射方向 i。

我们首先根据选用的 NDF模型，重要性采样微表面法向 m（也就是 i,o 之间的半程向量h），随后通过采样得到的微表面法向 m，利用反射关系来计算入射方向 i：

\[i = 2(m · o)m − o
\]

同时对于任意 NDF 下，采样 m 对应的概率密度 pdf m (m)，有:

\[pdf_m (m) = D(m)(m · n)
\]

(这是由 NDF 中

\(∫D(m)(m · n) = 1\) 这一性质得出，文档不会涉及到关于

NDF 性质的讨论。同样，关于下述 GGX 采样点生成的推导过程也会被略去)

通过该 \(pdf_m (m)\)，可以计算出 GGX NDF 对应的采样点应该为：

\[θ_m = arctan(
\frac{
α \sqrt{ξ_1}}
{\sqrt{1 − ξ_1}
}) \\
ϕ_h = 2πξ_2
\]

其中，ξ_1 ,ξ_2 ∈ [0,1)。

补充：

\[pdf_m (m) = D(m)(m · n) \\
= \frac{a^2}{PI*(((n \cdot h)^2)*(a^2-1)+1)^2} (n \cdot h) \\
= \frac{a^2}{PI*(cos^2 \theta*(a^2-1)+1)^2} cos \theta
\]

因为我们可以用球面坐标(\(\phi\),\(\theta\))表示半径向量m,因此我们可以把\(pdf_m\)表示为\(pdf_{\phi}\)和\(pdf_{\theta}\)的乘法。\(pdf_{\phi}\)不依赖角度\(\phi\),所以我们可以简单的推导出：

\[pdf_{\phi} = \frac{1}{2\pi}
\]

所以：

\[pdf_{\theta} = \frac{pdf_m(m)}{pdf_{\phi}} = \frac{2 a^2}{(cos^2 \theta*(a^2-1)+1)^2} cos \theta
\]

运用逆变换采样(Inverse Transform Sampling Method)生成具有指定概率密度分布的随机变量,我们需要先得到概率密度的累积分布，这里直接给出结果。

\[cdf_{\phi} = \int_{0}^{\phi}\frac{1}{2\pi}dx = \frac{1}{2 \pi} \phi \\
cdf_{\theta} = \int_0^{q} \frac{2a^2x}{(x^2(a^2-1)+1)^2} dx = \frac{1-q^2}{1+q^2(a^2-1)}
\]

其中 \(q=cos(\theta)\).现在反转cdf函数，以产生从均匀值\(\epsilon_1,\epsilon_2\)到角度\(\phi,\theta\)的映射：

\[\phi = \epsilon_1 * 2 \pi \\
\theta = arccos \sqrt{\frac{1-\epsilon_2}{1+\epsilon_2(a^2-1)}}
\]

或者

\[\theta = arctan \frac{a \sqrt{\epsilon_2}}{\sqrt{1-\epsilon_2}}
\]

两者是等价的。

第二个问题，如何计算采样得到的入射方向的概率。

因为我们最后生成的采

样方向是入射方向 i, 所以最后结果的权重应该是：

\[weight(i) = \frac
{f_r (i,o,h)(i,n)}
{pdf_i (i)}
\]

所以需要将之前采样微表面法线的概率密度 \(pdf_m (m)\) 转换成采样入射的概率密

度 \(pdf_i (i)\)，而两者之间的转换只需要简单的乘一个 Jacobian 项即可，即：

\[pdf_i (i) = pdf_m (m) ∥
\frac
{∂ω_m}
{∂ω_i}
∥
\]

其中，对于反射有：

\[∥
\frac
{∂ω_m}
{∂ω_i}
∥=
\frac
{1}
{4(i · m)}
\]

讨论完以上两点后，最终对于采样入射的权重可以整理为：

\[weight(i) = \frac
{(o · m)G(i,o,h)}
{(o · n)(m · n)}
\]

补充：

Jacobian项

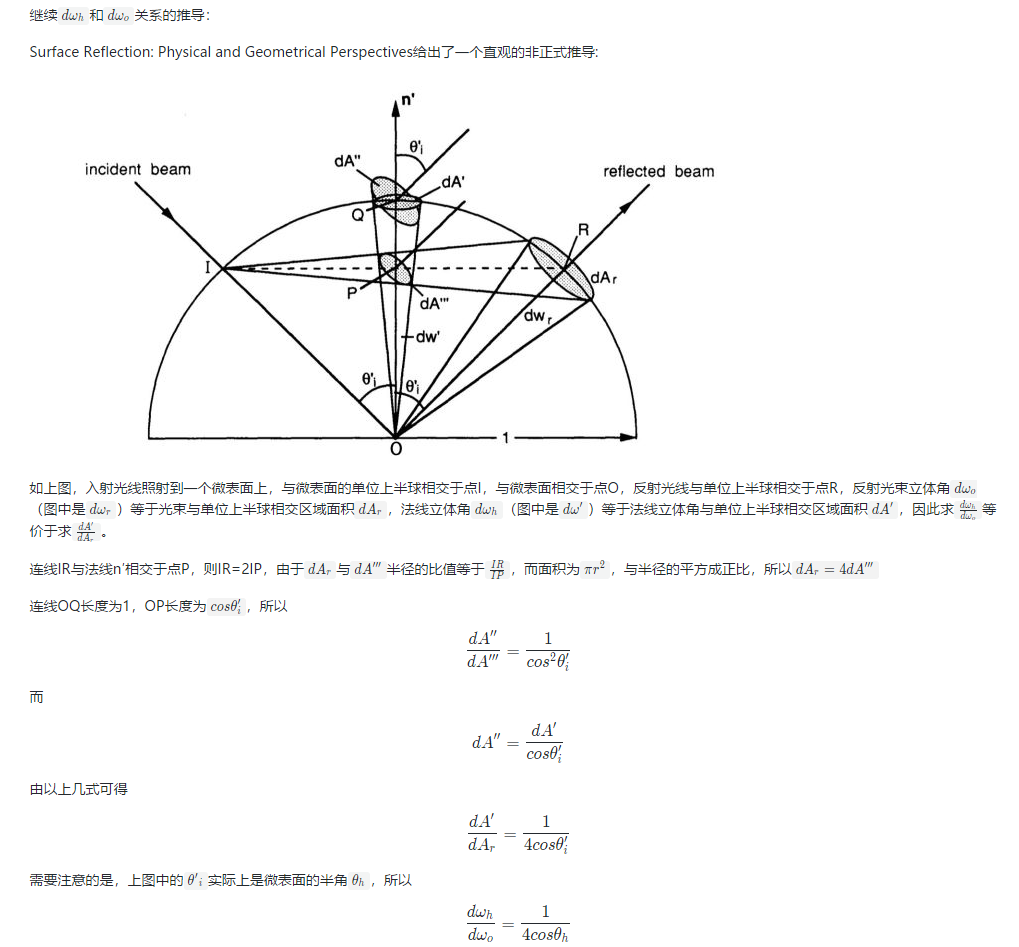
直观理解：

法线分布会以宏观法线为中心对应于一个波瓣lobe，在视线确定情况下，经过反射，反射光线又会形成于另一个波瓣。这两个波瓣的大小不同，因此对应点的概率密度分布也不同。

以一定概率任意取一个法线和以其中为中心的微小的立体角范围，会对应于另一个反射光线和其微小范围；这两个范围的光线的对应概率相等，因为它们直接是1-1映射的关系；又因为范围足够小，可以近似认为是概率密度在这个小区间均匀分布，因此：

\[pdf_h*A_h = pdf_o*A_o
\]

因此概率密度分布之比与微表面积之比成反比。