「模拟赛」A 层多校联训 4（卖品：CTH）

双倒一啦!

感觉这次最大的错误就是没看 T2。（本质原因还是时间浪费的太多了）

赛时记录在闲话啦

accoder 多校比赛链接

02 表示法

唐诗题！考高精的人都\(**\)，输出深度优先搜索解决。高精乘 2、高精减。

子串的子串

官方题解写的不好，放一下 Ratio 的好吃题解：

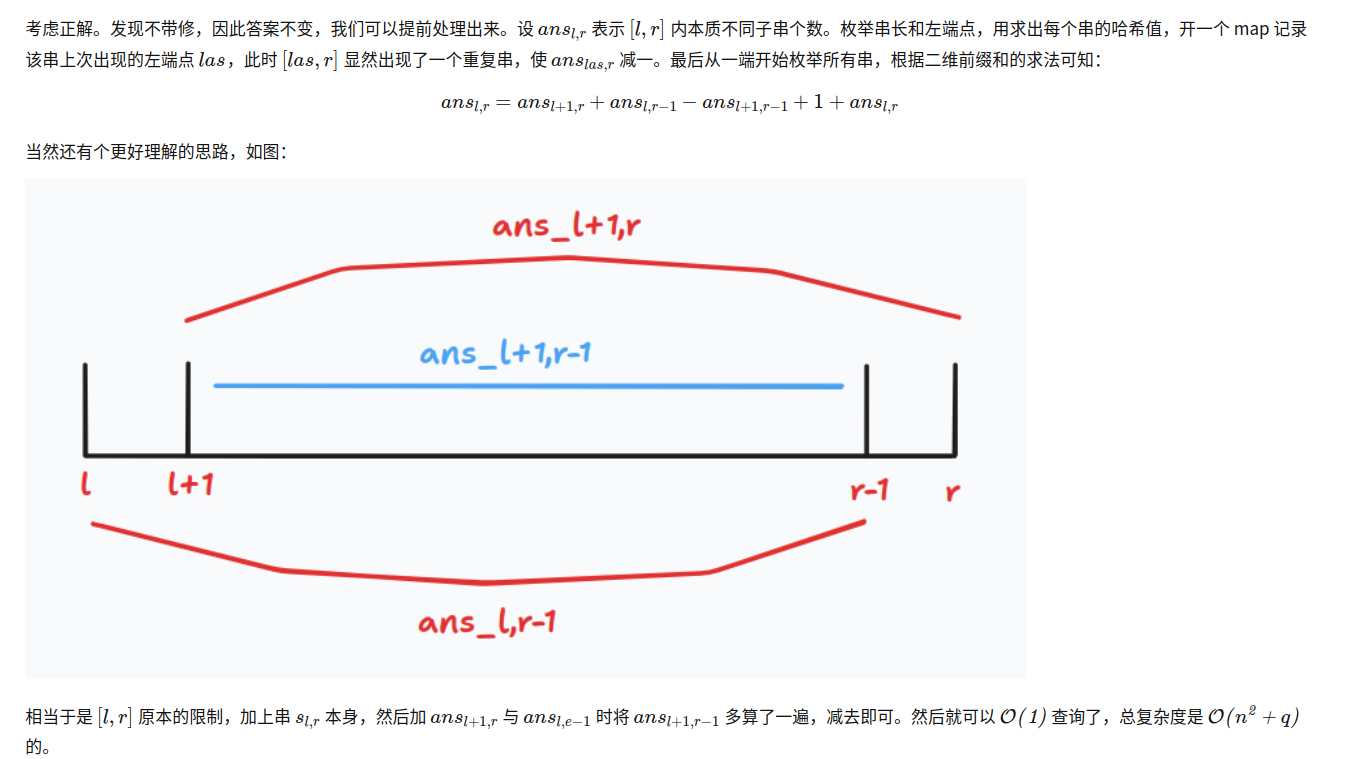
意思就是：\(ans_{l,r-1}\) 和 \(ans_{l+1,r}\) 中 包含重复的部分 \(ans_{l+1,r-1}\)，于是我们用 \(ans_{l,r-1} + ans_{l+1,r}-ans_{l+1,r-1}\) 来转移得到 \(ans_{l,r}\) 以避免重复，最后别忘了再加上字符串 \(s[l,r]\) 自己。

魔法咒语

trie 树

非官方题解思路：（CTH 巨佬的赛时思路，更好理解）

正序、倒序各建一颗 trie 树分别记为 \(tr1,tr2\)，那么所有前缀的个数就是 \(tr1\) 的节点数，后缀的个数就是 \(tr2\) 的节点数。

但直接相乘显然会有重复部分，比如两个字符串：abc 和 cd，前缀 abc 和 后缀 d 可以拼成一个字符串 abcd，同样前缀 ab 和 后缀 cd 也可以拼成abcd，有重复，考虑怎么减去这部分重复。

什么时候会有这样的重复呢？发现如果我们存在一个前缀的最后一个字符和一个后缀的第一个字符相同时，就会造成 1 个重复，因为 （该前缀删去最后一个字符加上该后缀） 与 （该前缀加上该后缀删去第一个字符）可以拼成相同的字符串。

但注意，我们所找的会造成重复的前缀和后缀不能只有一个字符（这样删去一个字符后就成空串了，但题目要求不为空）。

所以我们对于 26 个英文字母分别记它们作为前缀最后一个字符的个数 \(cntQ_{字母}\) 和 作为后缀第一个字符的个数 \(cntH_{字母}\)，保证这些前缀、后缀都是两个及以上的字符。

那么答案就是两棵树的节点数相乘减去 \(\sum _{i=26 个英文字母} cntQ_i\times cntH_i\)。

表达式

赛时最后五十分钟打了 45 部分分（不会 CRT），以为会很极限了，结果读入出锅保龄 RE 了。

部分分：

• \(15pts\)：暴力，每次询问从 \(1~n\) 算一遍就好了；

• \(5pts\)：每次询问时所有符号相同的情况，记一下所有数的加和 \(s\) 以及乘积 \(f\)，询问 \(x\) 时符号是 + 答案就是 \(x+s\)，是 * 答案就是 \(x\times f\)，是 ^ 答案就是 \(x^f\)；

• \(15 pts\)（但实际有 \(25pts\)）：对于没有 ^ 的样例，可以分块或者线段树简单维护就好，如果询问 \(x\) 时，序列可以转化为：\((k_1x+b_1)\times k_2+b_2=k_1k_2x+k_2b_1+b_2\)，那么 \(k_{new}=k_1k_2,b_{new}=k_2b_1+b_2\)，分块预处理出每个块的总 \(K\) 和 总 \(B\) 就好了，更新时把整个块重新遍历一遍，更新 \(K,B\) ，查询计算一遍所有块得到总的 \(k_总\) 和 \(b_总\)，代入 \(x\) 计算。

正解：

数据点分治

前三个点模数过大但数据范围小直接暴力。

其他的点对于模数特别小的，直接维护线段树上的点所有 \(x=[0,mod-1]\) 进入该点时得到的答案，时间复杂度大概是 \(O(qn\log n mod)\)。

而模数较大但是是合数的，把模数拆分成多个小一点的互质的数作为模数，对于每个模数分别像以上方式一样维护，最后 CRT 合并即可。

End

哦对，CTH 大佬无论讲题还是调题都巨棒呢，人也很热心，什么巨型数据结构啊，5k 以上代码啊，都欢迎来找 CTH 调捏