On the Optimization of Deep Networks: Implicit Acceleration by Overparameterization

目录

• 引
• 主要内容
  • 定理1
  • Claim 1
  • Claim 2
  • 定理2
• 证明
  • 定理1的证明
  • Claim 1 的证明
    • Kronecker product (克罗内克积)
  • Theorem 2 的证明
• 代码

Arora S, Cohen N, Hazan E, et al. On the Optimization of Deep Networks: Implicit Acceleration by Overparameterization[J]. arXiv: Learning, 2018.

引

我很喜欢这一篇文章，因为证明用到的知识并不难，但是却用的很巧，数学真是太牛了，这些人的嗅觉怎么这么好呢？

这篇文章，归根结底就是想说明一个问题，就是和一般的认知不同，随着神经网络的加深，参数更新的收敛速度并不会下降，感觉也有很多论文论述了深度depth的重要性.

不过，这篇文章，是在线性神经网络上做的一个分析，另外，标题中的Acceleration并没有很好的理论支撑，作者给出了几个特例和一些实验论据。我想作者肯定尝试过，但是想要证明想想就不易，至少得弄出个\(O(T^?)\)之类的.

虽然理论支撑不够，但是我感觉还是很厉害了.

主要内容

首先，为了排除一些干扰因素，就是Acceleration来自于俩个网络的表达能力不同，神经网络\(N_1,N_2\)， 如果二者的收敛速度不同，原因可能是\(N_1\)和\(N_2\)能让损失下降的程度不同. 而在线性网络中，层数增加并不会改变网络的表达能力.

\(L(W)\)是关于\(W\in \R^{k\times d}\)的损失函数，这个网络的表达能力和\(L(W_NW_{N-1}\cdots W_1)\)的表达能力是相同的，如果\(W_NW_{N-1}\cdots W_1\in \R^{k \times d}\).

对上面的结论，有一点点存疑，假设后者的最优为\((W_N^*, W_{N-1}^*,\ldots,W_1^*)\)，那么只要让\(W=W_N^* W_{N-1}^*\cdots W_1^*\)即可，所以\(L(W^*)\le L(W_N^* W_{N-1}^*\cdots W_1^*)\).

反过来似乎不一定，假设\(N=2\), \(W_2 \in \R^{k \times 1}, W_1 \in \R^{1 \times d}\), 但是利用here的结果，只要\(W_i\in \R^{d_i \times d_{i-1}}\), 满足\(d_i \ge \min \{k, d\}\)且\(L\)关于\(W\)为凸函数，就能说明等价. 居然还用上了之前看过的结果.

符号可能有点多，尽可能简化点吧. \(x \in \R^d\)为样本，\(y\in R^k\)为输出，

\[\Phi^N := \{ x \rightarrow W_NW_{N-1}\cdots W_1 x|W_j \in \R^{n_j \times n_{j-1}}, j=1,\cdots,N\},
\]

显然\(n_N=k,n_0=d\). 假设\(L^N(\cdot)\)是关于\((W_N,W_{N-1},\cdots, W_1)\)的函数, 可得

\[L^N(W_{N}, W_{N-1}, \ldots, W_1)=L^1(W_NW_{N-1}\cdots W_1),
\]

不要觉得这么做多此一举，不然后面证明的时候会弄乱的.

梯度下降采用了类似momentum的感觉，但是又有点不一样:

\[W_j^{(t+1)} \leftarrow (1-\eta \lambda)W_j^{(t)} - \eta \frac{\partial L^N}{\partial W_j}(W_1^{(t)},\ldots,W_N^{(t)}), \: j=1\ldots N.
\]

\(\eta>0\)的学习率，\(\lambda \ge 0\)是权重的递减系数.

定义

\[W_e = W_NW_{N-1}\cdots W_1,
\]

故\(L^N(W_N,\ldots,W_1)=L^1(W_e)\).

作者假设\(\eta\)，也就是学习率是一个小量，所以上面的式子可以从微分方程的角度去看

\[\dot{W}_j(t) = -\eta \lambda W_j(t) - \eta \frac{\partial L^N}{\partial W_j}(W_1^{(t)},\ldots,W_N^{(t)}).
\]

怎么说呢，这个所以，我的理解是\(\eta\)很小的时候，\(W_j(t)\)很平缓，所以可以认为导数和\(\Delta t=1\)的时候是一样的？

看了之前有一篇类似的Oja'rule也用了这种方法，感觉作者的意思应该是如果:

\[\dot{W}_j(t) = -\lambda W_j(t) - \frac{\partial L^N}{\partial W_j}(W_1^{(t)},\ldots,W_N^{(t)}),
\]

此时，

\[\begin{array}{ll}
{W}_j(t+\eta) &= W(t)-[\lambda W_j(t) + \frac{\partial L^N}{\partial W_j}(W_1^{(t)},\ldots,W_N^{(t)})]\eta+O(\eta^2)\\
&\approx(1-\eta \lambda)W_j^{(t)} - \eta \frac{\partial L^N}{\partial W_j}(W_1^{(t)},\ldots,W_N^{(t)}).
\end{array}
\]

我觉得应该是这个样子的，不过对于最后的结果没有影响.

定理1

定理1 假设权重矩阵\(W_1, \ldots W_N\)满足微分方程:

\[\dot{W}_j(t) = -\eta \lambda W_j(t) - \eta \frac{\partial L^N}{\partial W_j}(W_1^{(t)},\ldots,W_N^{(t)}), j=1,\ldots,N,
\]

且

\[W_{j+1}^T(t_0)W_{j+1}(t_0)=W_j(t_0)W_j^T(t_0), \: j=1,\ldots, N-1.
\]

则权重矩阵\(W_e\)的变化满足下列微分方程:

\[\begin{array}{ll}
\dot{W_e}(t) = & \eta \lambda N \cdot W_e(t) \\
& - \eta \sum_{j=1}^N [W_e(t) W_e^T(t)]^{\frac{j-1}{N}} \cdot \\
& \quad \frac{\mathrm{d}L^1}{\mathrm{d}W}(W_e(t))\cdot [W_e^T(t)W_e(t)]^{\frac{N-j}{N}}.
\end{array}
\]

其中\([\cdot]^{\frac{q}{p}}\)是关于半正定矩阵的一个定义，假如:

\[A = VDV^T, A^{\frac{q}{p}}=VD^{\frac{q}{p}}V^T,
\]

对角矩阵\(D^{\frac{q}{p}}\)是让对角线元素的\(D_{ii}^{\frac{q}{p}}\).

所以，权重\(W_e\)的更新变换近似于:

\[\begin{array}{ll}
{W_e}(t+1) = & (1-\eta \lambda N) \cdot W_e(t) \\
& - \eta \sum_{j=1}^N [W_e(t) W_e^T(t)]^{\frac{j-1}{N}} \cdot \\
& \quad \frac{\mathrm{d}L^1}{\mathrm{d}W}(W_e(t))\cdot [W_e^T(t)W_e(t)]^{\frac{N-j}{N}}.
\end{array}
\]

Claim 1

上面的更新实际上让人看不出一个所以然来，所以作者给出了一个向量形式的更新方式，可以更加直观地展现其中地奥秘.

Claim 1 对于任意矩阵\(A\), 定义\(vec(A)\)为由矩阵\(A\)按列重排后的向量形式. 于是，



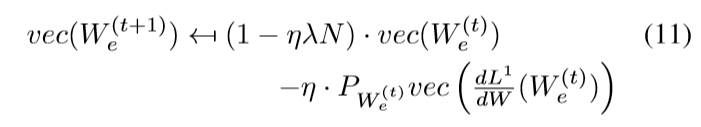
其中\(P_{W_e^{(t)}}\)是一个半正定矩阵，依赖于\(W_e\), 假设

\[W_e^{(t)}=UDV^T,
\]

其中\(U = [u_1,u_2, \ldots,u_k]\in \R^{k \times k}, V=[v_1,v_2,\ldots,v_d] \in \R^{d \times d}\), \(D\)的对角线元素，即\(W_e^{(t)}\)的奇异值从大到小为\(\sigma_1,\sigma_2,\ldots, \sigma_{\max \{k, d\}}\), 则\(P_{W_e^{(t)}}\)的特征向量和对应的特征值为:

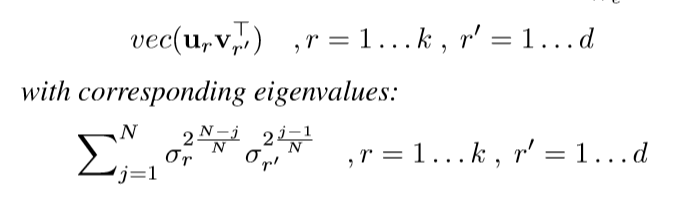
这说明了什么呢？也就是overparameterization后的更新，\(W_e^{(t+1)}\)的更新，也就是\(vec(W_e
^{(t+1)})\)的更新倾向于\(vec(u_1v_1^{T})\), 感觉这一点就和一些梯度下降方法的思想有点类似了，借用之前的成果. 而且，这个借用，会有一种坐标之间的互相沟通，一般的下降方法是不具备这一点的.

Claim 2

定理2

定理2 假设\(\frac{\mathrm{d}L^1}{\mathrm{d}W}\)在\(W=0\)处有定义，\(W=0\)的某个邻域内连续，那么对于给定的\(N \in \N, N > 2\), 定义:



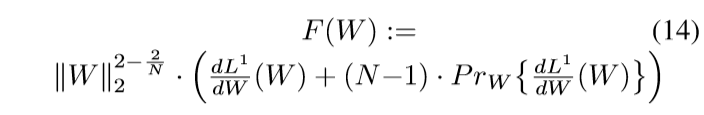
那么，不存在关于\(W\)的一个函数，其梯度场为\(F\).

定理2的意义在于，它告诉我们，overparameterization的方法是不能通过添加正则项来实现的，因为\(F(W)\)不存在原函数，所以诸如

\[L(W)+\lambda \|W\|
\]

的操作是不可能实现overparametrization的更新变化的.

证明思路是，构造一个封闭曲线，证明\(F(W)\)在其上的线积分不为0. （太帅了...)

证明

定理1的证明

首先是一些符号:

\[\prod_a^{j=b} W_j := W_b W_{b-1} \cdots W_a \\
\prod_{j=a}^b W_j^T := W_a^TW_{a+1}^T \cdots W_b^T
\]

用



表示块对角矩阵.

容易证明(其实费了一番功夫，但是不想写下来，因为每次都会忘，如果下次忘了，就再推一次当惩罚):

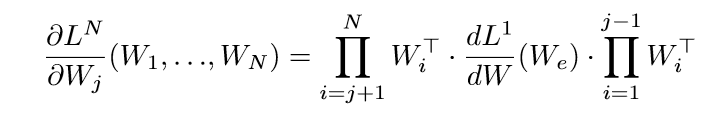
于是



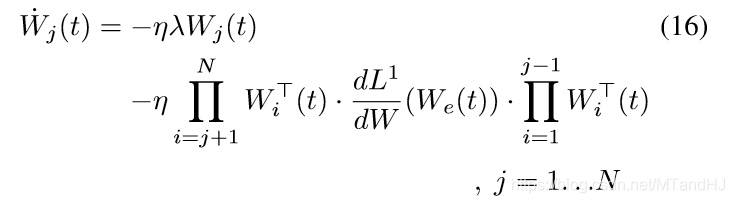
第\(j\)个等式俩边右乘\(W_j^T(t)\), 第\(j+1\)个等式俩边左乘\(W_{j+1}^T(t)\)可得：



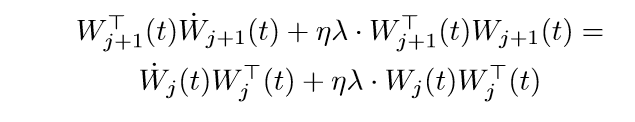
俩边乘以2

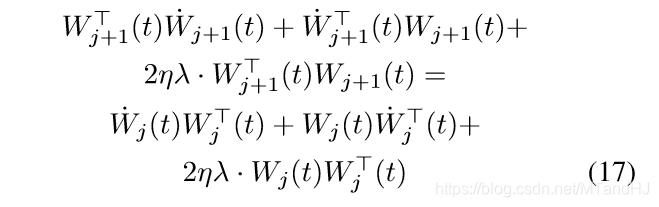
令\(C_j(t):=W_j(t)W_j^T(t), C_j'(t):=W_j^T(t)W_j(t)\), 则

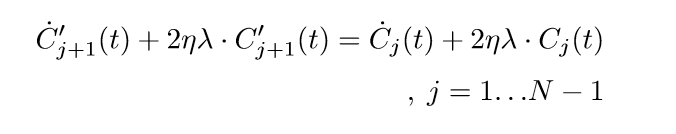
注意，我们将上面的等式改写以下，等价于

\[\dot{(C'_{j+1}-C_j)}(t) = -2\eta \lambda (C'_{j+1}-C_j)(t),
\]

用\(y(t):=(C'_{j+1}-C_j)(t)\), 则

\[\dot{y}(t)=-2\eta \lambda y,
\]

另外有初值条件\(y(t_0)=0\)(这是题设的条件).

容易知道，上面的微分方程的解为\(y\equiv0\).

所以

\[C'_{j+1}(t)=C_j(t), j=1,\ldots, N-1.
\]

假设\(W_j(t)\)的奇异值分解为

\[W_j(t)=U_j \Sigma_jV_j^T.
\]

且假设\(\Sigma_j\)的对角线元素，即奇异值是从大到小排列的.

则可得

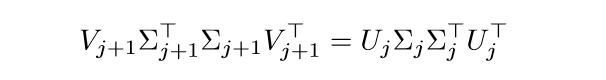
显然\(\Sigma_{j+1}^T\Sigma_{j+1}=\Sigma_j \Sigma_j^T\), 这是因为一个矩阵的特征值是固定的（如果顺序固定的话），特征向量是不一定的，因为可能有多个相同的特征值，那么对于一个特征值的子空间的任意正交基都可以作为特征向量，也就是说

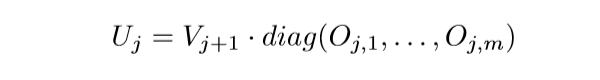
其中\(I_{d_r} \in \R^{d_r \times d_r}\)是单位矩阵, \(O_{j,r} \in \R^{d_r \times d_r}\)是正交矩阵.

所以对于\(j=1\ldots N-1\), 成立

\(j=N\)有



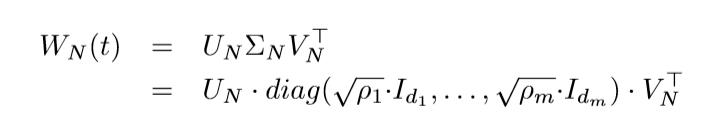
故



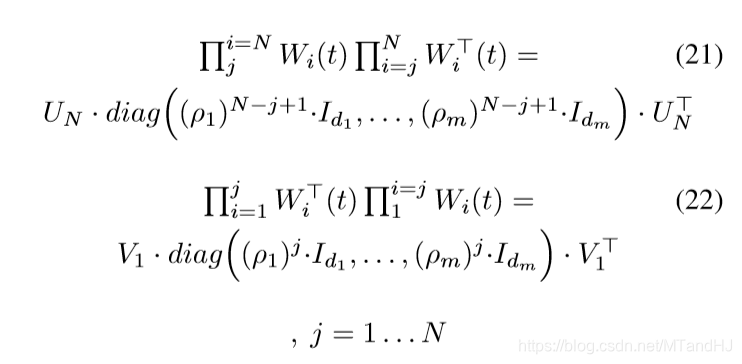
注意，上面的推导需要用到:

\[(diag(O_{j,1},\ldots, O_{j,m}))^T diag((\rho_1)^c I_{d_1},\ldots, (\rho_,)^j I_{d_m})(diag(O_{j,1},\ldots, O_{j,m})) = diag((\rho_1)^c I_{d_1},\ldots, (\rho_,)^j I_{d_m})
\]

既然



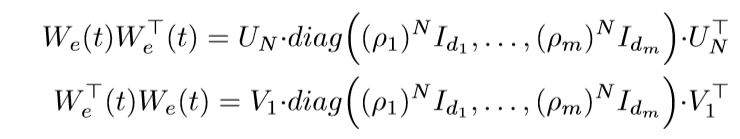
那么





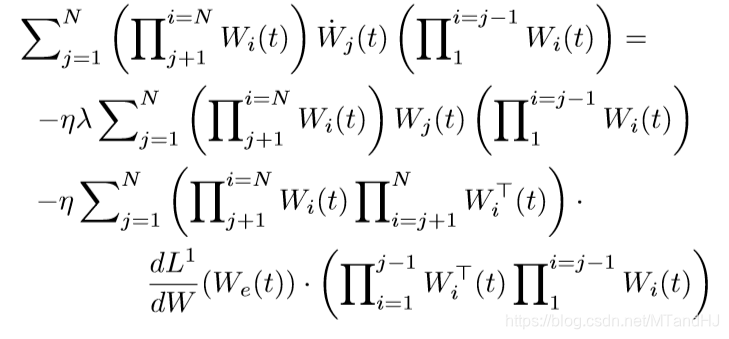
上式左端为\(\dot{W}_e(t)\), 于是

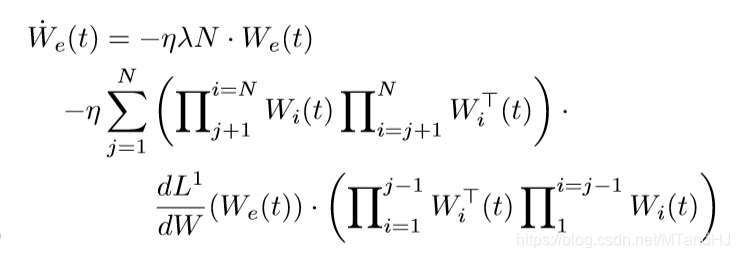
再利用（23）（24）的结论

Claim 1 的证明

Kronecker product (克罗内克积)

网上似乎都用\(\otimes\), 不过这里还是遵循论文的使用规范吧， 用\(\odot\)来表示Kronecker product:

\[A \odot B :=
\left [
\begin{array}{ccc}
a_{11} \cdot B & \cdots & a_{1n_{a}} \cdot B \\
\vdots & \ddots & \vdots \\
a_{m_a1} \cdot B & \cdots & a_{m_a n_a} \cdot B
\end{array}
\right ] \in \R^{m_am_b \times n_an_b},
\]

其中\(A \in \R^{m_a \times n_a}, B \in \R^{m_b \times n_b}\).

容易证明 \(A \odot B\)的第\(rn_b + s, r = 0, 1, \ldots, n_a-1, s = 0, 1, \ldots, n_b-1\)列为:

\[vec(B_{*s+1}A_{*r+1}^T),
\]

其中\(B_{*j}\)表示\(B\)的第\(j\)列, 沿用\(vec(A)\)为\(A\)的列展开. 相应的，\(A \odot B\)的第\(pm_b+q, p=0,1,\ldots,m_a-1,q=0, 1, \ldots, m_b-1\)行为:

\[vec(B_{q+1*}^TA_{p+1*})^T,
\]

其中\(A_{i*}\)表示\(A\)的第\(i\)行.

用\([A\odot B]_{(p,q,r,s)}\)表示\([A \odot B]\)的第\(rn_b+s\)列\(pm_b+q\)行的元素, 则

\[[A\odot B]_{(p,q,r,s)} = a_{p+1,r+1}b_{q+1,s+1}
\]

另外\(I_{d_1} \odot I_{d_2} = I_{d_1d_2}\).

下面再证明几个重要的性质:

\((A_1 \odot A_2)(B_1 \odot B_2) = (A_1 B_1) \odot (A_2B_2)\)

假设\(A_1 \in \R^{m_1 \times l_1}, B_1 \in \R^{l_1 \times n_1}, A_2 \in \R^{m_2 \times l_2}, B_2 \in \R^{l_2 \times n_2}\), 则

\[(A_1 \odot A_2)(B_1 \odot B_2) = (A_1 B_1) \odot (A_2B_2)
\]

考察俩边矩阵的\((pm_2+q,rn_2+s)\)的元素，

\[\begin{array}{ll}
[(A_1 \odot A_2)(B_1 \odot B_2)]_{(p,q,r,s)} &= (A_1 \odot A_2)_{pm_2+q*} (B_1 \odot B_2)_{*rn_2+s} \\
&= vec({A_2}_{q+1*}^T{A_1}_{p+1*})^T vec({B_2}_{*s+1}{B_1}_{*r+1}) \\
& = tr({A_1}_{p+1*}^T{A_2}_{q+1*}{B_2}_{*s+1}{B_1}_{*r+1}^T) \\
& = ({A_1}_{p+1*}{B_1}_{*r+1}) ({A_2}_{q+1*}{B_2}_{*s+1}) \\
& = (A_1B_1)_{p+1,r+1} (A_2B_2)_{q+1,s+1} \\
& = [(A_1 B_1) \odot (A_2B_2)]_{(p,q,r,s)}.
\end{array}
\]

得证. 注意，倒数第四个等式到倒数第三个用到了迹的可交换性.

\((A \odot B)^T=A^T \odot B^T\)

\[\begin{array}{ll}
[(A \odot B)^T]_{(p, q, r, s)} &= [A \odot B]_{(r, s, p, q)} = a_{r+1,p+1}b_{s+1,q+1} \\
& = a^T_{p+1,r+1}b^T_{q+1,s+1}=[A^T \odot B^T]_{(p,q,r,s)}.
\end{array}
\]

\(A^T=A^{-1},B^T=B^{-1} \Rightarrow (A \odot B)^T = (A \odot B)^{-1}\)

\[\begin{array}{ll}
(A \odot B)^T(A \odot B) & = (A^T \odot B^T)(A \odot B) \\
&= (A^TA) \odot (B^TB) \\
&= I_{n_a} \odot I_{n_b} \\
& = I_{n_a n_b},
\end{array}
\]

所以\((A \odot B)^T = (A \odot B)^{-1}\).

回到Claim 1 的证明上来，容易证明



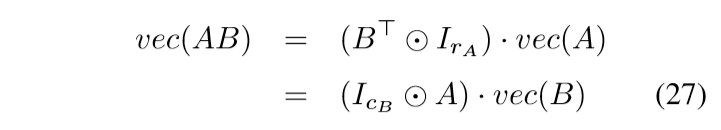
于是



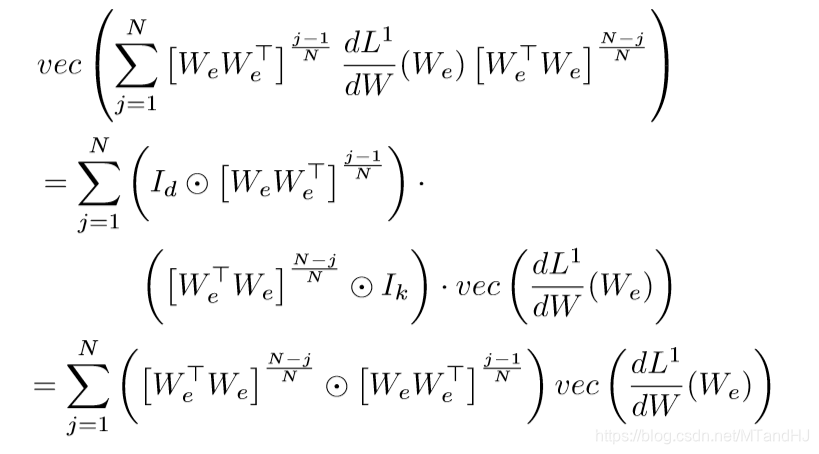
第二个等式用到了\((A_1 \odot A_2)(B_1 \odot B_2) = (A_1 B_1) \odot (A_2B_2)\).

只需要证明：

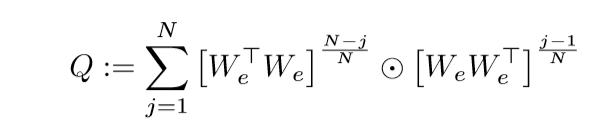
等价于\(P_{W_e}\). 令

\[W_e = UDV^T,
\]

其中\(U \in \R^{k \times k}, V \in \R^{d \times d}\).

所以

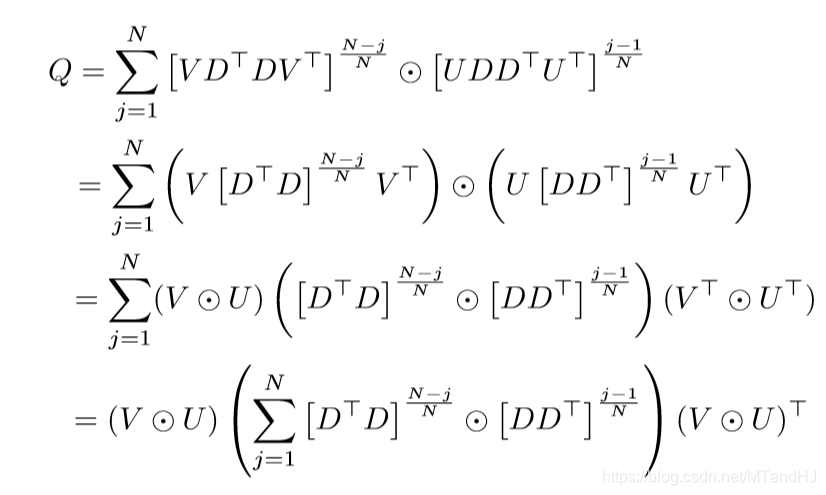
第三个等式用了俩次\((A_1 \odot A_2)(B_1 \odot B_2) = (A_1 B_1) \odot (A_2B_2)\).

定义:

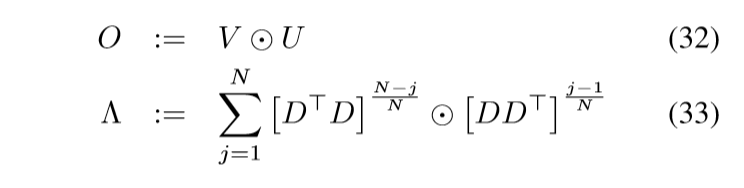
则

\[Q = O \Lambda O^T.
\]

剩下的，关于\(O\)的列



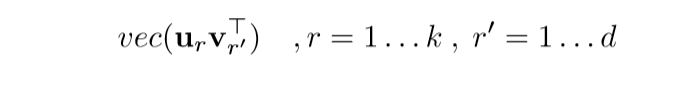
\(\Lambda\)的对角元素:



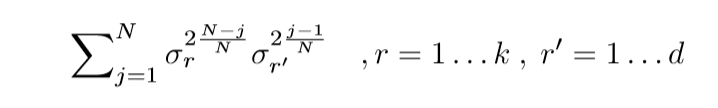
只是一些简单的推导罢了.

Theorem 2 的证明

这个证明我不想贴在这里，因为这个证明我只能看懂，所以想知道就直接看原文吧.

代码

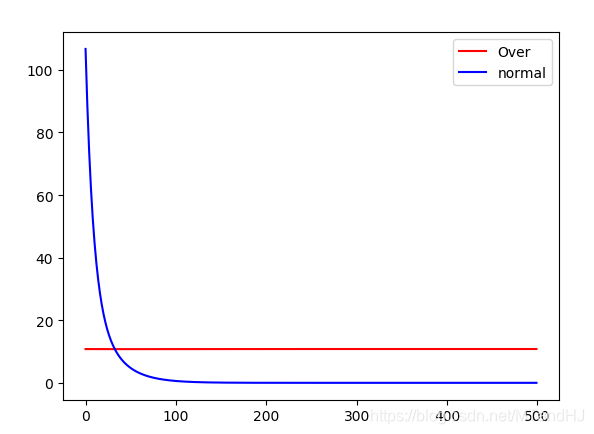
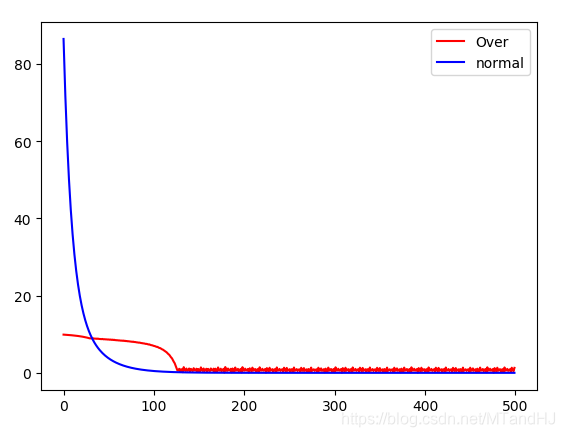
虽然只是用了一个很简单的例子做实验，但是感觉，这个迭代算法很吃初始值. 就像Claim 1 所解释的那样，这个下降方法，会更倾向于之前的方向，也就是之前的错了，后面也会错？

y1设置为100， y2设置为1， lr=0.005, 会出现（也有可能是收敛不到0):

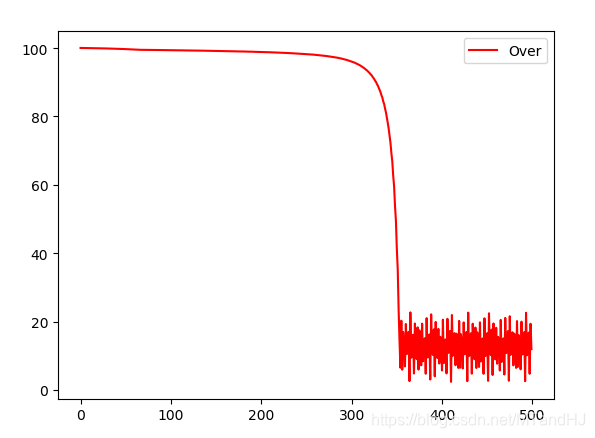
这种下降的方式是蛮恐怖的啊，但是感觉实在是不稳定. 当然，也有可能是程序写的太烂了.

"""
On the Optimization of Deep
Net works: Implicit Acceleration by
Overparameterization
"""

import numpy as np
import torch
import torch.nn as nn
from torch.optim.optimizer import Optimizer, required

class Net(nn.Module):
    def __init__(self, d, k):
        """
        :param k:  输出维度
        :param d:  输入维度
        """
        super(Net, self).__init__()
        self.d = d
        self.dense = nn.Sequential(
            nn.Linear(d, k)
        )

    def forward(self, input):
        x = input.view(-1, self.d)
        output = self.dense(x)
        return output

class Overparameter(Optimizer):
    def __init__(self, params, N, lr=required, weight_decay=1.):
        defaults = dict(lr=lr)
        super(Overparameter, self).__init__(params, defaults)
        self.N = N
        self.weight_decay = weight_decay

    def __setstate__(self, state):
        super(Overparameter, self).__setstate__(state)
        print("????")
        print(state)
        print("????")

    def step(self, colsure=None):
        def calc_part2(W, dw, N):
            dw = dw.detach().numpy()
            w = W.detach().numpy()
            norm = np.linalg.norm(w, 2)
            part2 = norm ** (2-2/N) * (
                dw +
                (N - 1) * (w @ dw.T) * w / (norm ** 2 + 1e-5)
            )
            return torch.from_numpy(part2)

        p = self.param_groups[0]['params'][0]
        if p.grad is None:
            return 0
        d_p = p.grad.data
        part1 = (self.weight_decay * p.data).float()
        part2 = (calc_part2(p, d_p, self.N)).float()
        p.data -= self.param_groups[0]['lr'] * (part1+part2)

        return 1

class L4Loss(nn.Module):
    def __init__(self):
        super(L4Loss, self).__init__()

    def forward(self, x, y):
        return torch.norm(x-y, 4)

x1 = torch.tensor([1., 0])
y1 = torch.tensor(10.)
x2 = torch.tensor([0, 1.])
y2 = torch.tensor(2.)
net = Net(2, 1)
criterion = L4Loss()
opti = Overparameter(net.parameters(), 4, lr=0.01)

loss_store = []
for epoch in range(500):
    running_loss = 0.0
    out1 = net(x1)
    loss1 = criterion(out1, y1)
    opti.zero_grad()
    loss1.backward()
    opti.step()
    running_loss += loss1.item()
    out2 = net(x2)
    loss2 = criterion(out2, y2)
    opti.zero_grad()
    loss2.backward()
    opti.step()
    running_loss += loss2.item()
    #print(running_loss)
    loss_store.append(running_loss)

net = Net(2, 1)
criterion = nn.MSELoss()
opti = torch.optim.SGD(net.parameters(), lr=0.01)
loss_store2 = []
for epoch in range(500):
    running_loss = 0.0
    out1 = net(x1)
    loss1 = criterion(out1, y1)
    opti.zero_grad()
    loss1.backward()
    opti.step()
    running_loss += loss1.item()
    out2 = net(x2)
    loss2 = criterion(out2, y2)
    opti.zero_grad()
    loss2.backward()
    opti.step()
    running_loss += loss2.item()
    #print(running_loss)
    loss_store2.append(running_loss)

import matplotlib.pyplot as plt

plt.plot(range(len(loss_store)), loss_store, color="red", label="Over")
plt.plot(range(len(loss_store2)), loss_store2, color="blue", label="normal")
plt.legend()
plt.show()