51Nod 1264：线段相交（计算几何）

51Nod 1264：线段相交

Decision

给出平面上两条线段的两个端点，判断这两条线段是否相交（有一个公共点或有部分重合认为相交）。 如果相交，输出"Yes"，否则输出"No"。

Input

第1行：一个数T，表示输入的测试数量(1 <= T <= 1000)

第2 - T + 1行：每行8个数，x1,y1,x2,y2,x3,y3,x4,y4。(-10^8 <= xi, yi <= 10^8)

(直线1的两个端点为x1,y1 | x2, y2,直线2的两个端点为x3,y3 | x4, y4)

Output

输出共T行，如果相交输出"Yes"，否则输出"No"。

输入样例

2
1 2 2 1 0 0 2 2
-1 1 1 1 0 0 1 -1

输出样例

Yes
No

Solve

跨立实验

如果两线段相交，则两线段必然相互跨立对方。若P1P2跨立Q1Q2 ，则矢量 ( P1 - Q1 ) 和( P2 - Q1 )位于矢量( Q2 - Q1 ) 的两侧，即( P1 - Q1 ) × ( Q2 - Q1 ) * ( P2 - Q1 ) × ( Q2 - Q1 ) < 0。上式可改写成( P1 - Q1 ) × ( Q2 - Q1 ) * ( Q2 - Q1 ) × ( P2 - Q1 ) > 0。当 ( P1 - Q1 ) × ( Q2 - Q1 ) = 0 时，说明 ( P1 - Q1 ) 和 ( Q2 - Q1 )共线，但是因为已经通过快速排斥试验，所以 P1 一定在线段 Q1Q2上；同理，( Q2 - Q1 ) ×(P2 - Q1 ) = 0 说明 P2 一定在线段 Q1Q2上。所以判断P1P2跨立Q1Q2的依据是：( P1 - Q1 ) × ( Q2 - Q1 ) * ( Q2 - Q1 ) × ( P2 - Q1 ) >= 0。同理判断Q1Q2跨立P1P2的依据是：( Q1 - P1 ) × ( P2 - P1 ) * ( P2 - P1 ) × ( Q2 - P1 ) >= 0。具体情况如下图所示：



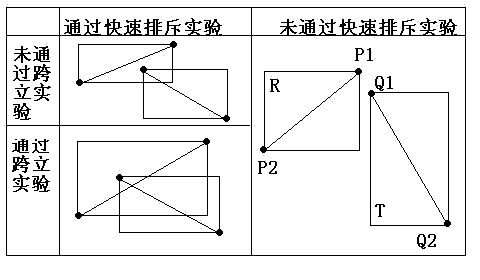
（以上摘自 [https://dev.gameres.com/Program/Abstract/Geometry.htm#判断两线段是否相交]）

Code

/*************************************************************************

	 > Author: WZY
	 > School: HPU
	 > Created Time:   2019-06-25 17:43:54

************************************************************************/
#include <bits/stdc++.h>
#define ll long long
#define ull unsigned long long
#define ms(a,b) memset(a,b,sizeof(a))
const int inf=(1<<30);
const ll INF=(1LL*1<<60);
const int maxn=1e6+10;
const int mod=1e9+7;
const int maxm=1e3+10;
using namespace std;
struct node
{
	double x,y;
}p[maxn];
double cel(node a,node b,node c)
{
	return (a.x-c.x)*(b.y-c.y)-(a.y-c.y)*(b.x-c.x);
}
int main(int argc, char const *argv[])
{
	#ifndef ONLINE_JUDGE
	    freopen("in.txt", "r", stdin);
	    freopen("out.txt", "w", stdout);
	#endif
	ios::sync_with_stdio(false);
	cin.tie(0);
	int t;
	cin>>t;
	while(t--)
	{
		for(int i=0;i<4;i++)
			cin>>p[i].x>>p[i].y;
		if(cel(p[0],p[1],p[2])*cel(p[0],p[1],p[3])<=0&&cel(p[2],p[3],p[0])*cel(p[2],p[3],p[1])<=0)
			cout<<"Yes\n";
		else
			cout<<"No\n";
	}
	return 0;
}