[CTF]维吉尼亚密码(维基利亚密码)

----------------------百度百科

https://baike.baidu.com/item/维吉尼亚密码/4905472?fr=aladdin

维吉尼亚密码（又译维热纳尔密码）是使用一系列凯撒密码组成密码字母表的加密算法，属于多表密码的一种简单形式。

中文名	维吉尼亚密码
外文名	Vigenère cipher
出处	吉奥万巴蒂斯塔贝拉索先生的密码

性质	加密算法
名词解释	恺撒密码的基础上扩展的多表密码
组成元素	明文、密钥、密表

描述

在一个凯撒密码中，字母表中的每一字母都会作一定的偏移，例如偏移量为3时，A就转换为了D、B转换为了E……而维吉尼亚密码则是由一些偏移量不同的恺撒密码组成。

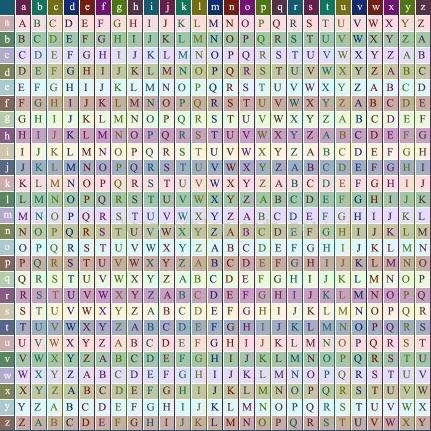
为了生成密码，需要使用表格法。这一表格（如图1所示）包括了26行字母表，每一行都由前一行向左偏移一位得到。具体使用哪一行字母表进行编译是基于密钥进行的，在过程中会不断地变换。

图1.表格

例如，假设明文为：

ATTACKATDAWN

选择某一关键词并重复而得到密钥，如关键词为LEMON时，密钥为：

LEMONLEMONLE

对于明文的第一个字母A，对应密钥的第一个字母L，于是使用表格中L行字母表进行加密，得到密文第一个字母L。类似地，明文第二个字母为T，在表格中使用对应的E行进行加密，得到密文第二个字母X。以此类推，可以得到：

明文：ATTACKATDAWN密钥：LEMONLEMONLE密文：LXFOPVEFRNHR

解密的过程则与加密相反。例如：根据密钥第一个字母L所对应的L行字母表，发现密文第一个字母L位于A列，因而明文第一个字母为A。密钥第二个字母E对应E行字母表，而密文第二个字母X位于此行T列，因而明文第二个字母为T。以此类推便可得到明文。

用数字0-25代替字母A-Z，维吉尼亚密码的加密文法可以写成同余的形式：

解密方法则能写成：

密码破译

对包括维吉尼亚密码在内的所有多表密码的破译都是以字母频率为基础的，但直接的频率分析却并不适用。例如，如果P是密文中出现次数最多的字母，则P很有可能对应E（前提是明文的语言为英语）。原因在于E是英语中使用频率最高的字母。然而，由于在维吉尼亚密码中，E可以被加密成不同的密文，因而简单的频率分析在这里并没有用。

破译维吉尼亚密码的关键在于它的密钥是循环重复的。如果我们知道了密钥的长度，那密文就可以被看作是交织在一起的凯撒密码，而其中每一个都可以单独破解。使用卡西斯基试验和弗里德曼试验来得到密钥的长度。

卡西斯基试验

弗里德里希·卡西斯基于1863年首先发表了完整的维吉尼亚密码的破译方法，称为卡西斯基试验（Kasiski examination）。早先的一些破译都是基于对于明文的认识、或者使用可识别的词语作为密钥。而卡西斯基的方法则没有这些限制。然而，在此之前，已经有人意识到了这一方法。1854年，查尔斯·巴贝奇受到斯维提斯（John Hall Brock Thwaites）在《艺术协会杂志》（Journal of the Society of the Arts）上声称发明了“新密码”的激励，从而破译了维吉尼亚密码。巴贝奇发现斯维提斯的密码只不过是维吉尼亚密码的一个变种而已，而斯维提斯则向其挑战，让他尝试破译用两个不同长度的密钥加密的密文。巴贝奇成功地进行了破译，得到的明文是丁尼生所写的诗《罪恶的想象》（The Vision of Sin），使用的密钥则是丁尼生妻子的名字Emily（艾米莉）。巴贝奇从未对他的方法进行过解释。在对巴贝奇生前笔记的研究中发现，早在1846年巴贝奇就使用了这一方法，与后来卡西斯基发表的方法相同。

卡西斯基试验是基于类似the这样的常用单词有可能被同样的密钥字母进行加密，从而在密文中重复出现。例如，明文中不同的CRYPTO可能被密钥ABCDEF加密成不同的密文：

密钥：ABCDEF AB CDEFA BCD EFABCDEFABCD

明文：CRYPTO IS SHORT FOR CRYPTOGRAPHY

密文：CSASXT IT UKSWT GQU GWYQVRKWAQJB

此时明文中重复的元素在密文中并不重复。然而，如果密钥相同的话，结果可能便为（使用密钥ABCD）：

密钥：ABCDAB CD ABCDA BCD ABCDABCDABCD

明文：CRYPTO IS SHORT FOR CRYPTOGRAPHY

密文：CSASTP KV SIQUT GQU CSASTPIUAQJB

此时卡西斯基试验就能产生效果。对于更长的段落此方法更为有效，因为通常密文中重复的片段会更多。如通过下面的密文就能破译出密钥的长度：

密文：DYDUXRMHTVDVNQDQNWDYDUXRMHARTJGWNQD

其中，两个DYDUXRMH的出现相隔了18个字母。因此，可以假定密钥的长度是18的约数，即长度为18、9、6、3或2。而两个NQD则相距20个字母，意味着密钥长度应为20、10、5、4或2。取两者的交集，则可以基本确定密钥长度为2。

弗里德曼试验

弗里德曼试验由威廉·F·弗里德曼（William F. Friedman）于1920年代发明。他使用了重合指数（index of coincidence）来描述密文字母频率的不匀性，从而破译密码。

指目标语言中两个任意字母相同的概率（英文中为0.067），

指字母表中这种情况出现的概率（英文中为1/26=0.0385），从而密钥长度可以估计为：

其中，观察概率为

其中，c是指字母表的长度（英文为26），N指文本的长度，n1到nc是指密文的字母频率，为整数。

此方法只是一种估计，会随着文本长度的增加而更为精确。在实践中，会尝试接近此估计的多个密钥长度。一种更好的方法是将密文写成矩阵形式，其中列数与假定的密钥长度一致，将每一列的重合指数单独计算，并求得平均重合指数。对于所有可能的密钥长度，平均重合指数最高的最有可能是真正的密钥长度。这样的试验可以作为卡西斯基试验的补充。 [3]

频率分析

一旦能够确定密钥的长度，密文就能重新写成多列，列数与密钥长度对应。这样每一列其实就是一个凯撒密码，而此密码的密钥（偏移量）则对应于维吉尼亚密码密钥的相应字母。与破译凯撒密码类似的方法，就能将密文破译。

柯克霍夫方法作为卡西斯基试验的改进，由奥古斯特·柯克霍夫（Auguste Kerckhoffs）提出。它将每一列的字母频率与转换后的明文频率相对应而得出每一列的密钥字母。一旦密钥中每一个字母都能确定，就能很简单地破译密文，从而得到明文。如果维吉尼亚字母表表格本身是杂乱而非按通常字母表顺序的话，那柯克霍夫方法就会无效，但卡西斯基试验和重复指数对于决定密钥长度仍旧是有效的。

变体

维吉尼亚密码的变体滚动密钥密码也曾一度被认为是不可破译的。这种变体的密钥与密文的长度一致，因此卡西斯基试验和弗里德曼试验即变得无效。1920年，弗里德曼首先发现了此方法的弱点。由于滚动密钥密码的密钥是一段真实的语言，因而破译者便能了解密钥文本的统计信息，而这种信息也会反映到密文当中。

如果密钥是完全随机、与明文的长度一致且只使用过一次，维吉尼亚密码理论上是不可破译的。然而，这种情况下密钥本身而非密文便成了关键，这被称为一次性密码本。

维吉尼亚本人确实发明了一种更强的维吉尼亚密码变体——自动密钥密码。巴贝奇所破译的其实是这种自动密钥密码，而卡西斯基则通常被认为是首先发表了破译固定密钥多表密码的方法。

还有一种简单的变体使用维吉尼亚的解码方法进行加密，同时使用维吉尼亚的加密方法进行解密，这被称为变异博福特密码。此方法与弗朗西斯·博福特创造的博福特密码不同，后者虽然也与维吉尼亚密码相似，但使用了修改过的加密方式和表格，是一种对等加密。

维吉尼亚密码表面上的强度并没能使其在欧洲得到广泛使用。由Gronsfeld伯爵所创造的Gronsfeld密码基本与维吉尼亚密码相同，不过它只使用10个不同的密码字母表（对应字母0到9）。Gronsfeld密码的强度很高，这是因为它的密钥并不是一个单词，但缺点在于字母表数量过少。尽管如此，Gronsfeld密码仍在德国和整个欧洲有着广泛的应用。