DL4J实战之五：矩阵操作基本功

欢迎访问我的GitHub

https://github.com/zq2599/blog_demos

内容：所有原创文章分类汇总及配套源码，涉及Java、Docker、Kubernetes、DevOPS等；

本篇概览

• 作为《DL4J实战》系列的第五篇，在前面对深度学习有一定的了解后，本篇会暂停深度学习相关的操作，转为基本功练习：矩阵操作，即INDArray接口的基本用法
• INDArray的类图如下，由于BaseNDArray是个抽象类，因此在实际使用中，咱们用的都是NDArray的实例：

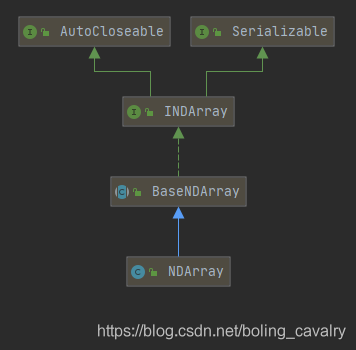
• 之所以用一篇文章来学习矩阵操作，是因为后面的实战过程中处处都有它，处处离不开它，若不熟练就会寸步难行；

• 本篇涉及的API较多，因此先做好归类，后面的代码按照分类来写会清晰一些，一共分为五类：矩阵属性、创建操作、读操作、写操作、矩阵计算，接下来用思维导图列出每一类的常用API

• 矩阵属性：

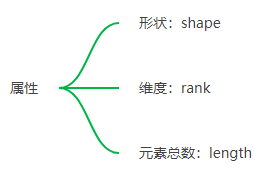
• 创建操作：

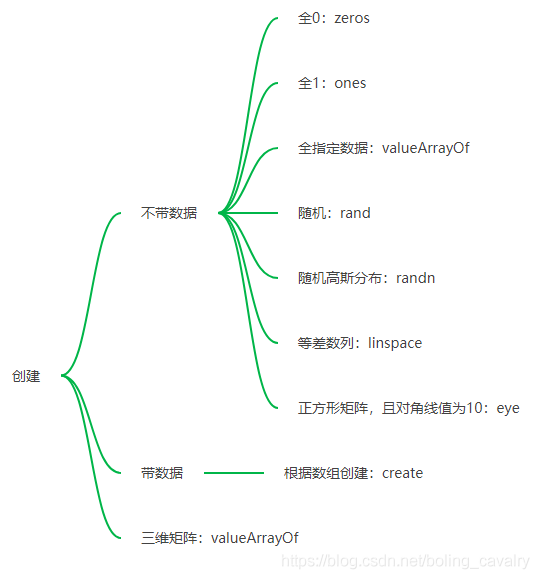
• 读操作：

• 写操作：

• 矩阵计算：

源码下载

• 本篇实战中的完整源码可在GitHub下载到，地址和链接信息如下表所示(https://github.com/zq2599/blog_demos)：

名称	链接	备注
项目主页	https://github.com/zq2599/blog_demos	该项目在GitHub上的主页
git仓库地址(https)	https://github.com/zq2599/blog_demos.git	该项目源码的仓库地址，https协议
git仓库地址(ssh)	git@github.com:zq2599/blog_demos.git	该项目源码的仓库地址，ssh协议

• 这个git项目中有多个文件夹，《DL4J实战》系列的源码在dl4j-tutorials文件夹下，如下图红框所示：

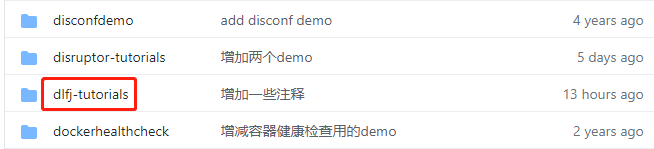
• dl4j-tutorials文件夹下有多个子工程，本次实战代码在ndarray-experience目录下，如下图红框：

创建工程

• 在父工程dl4j-tutorials下新建名为ndarray-experience的子工程，其pom.xml如下：

<?xml version="1.0" encoding="UTF-8"?>
<project xmlns="http://maven.apache.org/POM/4.0.0"
         xmlns:xsi="http://www.w3.org/2001/XMLSchema-instance"
         xsi:schemaLocation="http://maven.apache.org/POM/4.0.0 http://maven.apache.org/xsd/maven-4.0.0.xsd">
    <parent>
        <artifactId>dlfj-tutorials</artifactId>
        <groupId>com.bolingcavalry</groupId>
        <version>1.0-SNAPSHOT</version>
    </parent>
    <modelVersion>4.0.0</modelVersion>

    <artifactId>ndarray-experience</artifactId>

    <dependencies>
        <dependency>
            <groupId>org.nd4j</groupId>
            <!--注意要用nd4j-native-platform，否则容器启动时报错：no jnind4jcpu in java.library.path-->
            <artifactId>${nd4j.backend}</artifactId>
        </dependency>

        <dependency>
            <groupId>ch.qos.logback</groupId>
            <artifactId>logback-classic</artifactId>
        </dependency>
    </dependencies>

</project>

• 接下来的代码都写在ndarray-experience工程中

最基本的方法

• 先列出两个最基本的方法，后面学习时会频繁用到它们：

• rand：秩，维数，例如2行3列的二维矩阵，rand方法返回值等于2

• shape：矩阵每个维度的大小，如2行3列的二维矩阵，shape方法返回值等于[2, 3]

• 准备一个静态方法，可以将INDArray实例的详情打印出来，用的就是rand和shape方法：

    private static void disp(String type, INDArray indArray) {
        StringBuilder stringBuilder = new StringBuilder("*****************************************************\n");
        stringBuilder.append(type)
                     .append("\n维度 : ").append(indArray.rank())
                     .append("\n形状 : ").append(Arrays.toString(indArray.shape()))
                     .append("\n完整矩阵 : \n").append(indArray);

        System.out.println(stringBuilder);
    }

创建矩阵

1. 全零矩阵：zeros

// 创建2行3列的全零矩阵
INDArray indArray0 = Nd4j.zeros(2, 3);
disp("全零矩阵", indArray0);

• 执行结果

全零矩阵
维度 : 2
形状 : [2, 3]
完整矩阵 :
[[         0,         0,         0],
 [         0,         0,         0]]

1. 全1矩阵：ones

// 创建2行3列的全一矩阵
INDArray indArray1 = Nd4j.ones(2, 3);
disp("全一矩阵", indArray1);

• 执行结果

全一矩阵
维度 : 2
形状 : [2, 3]
完整矩阵 :
[[    1.0000,    1.0000,    1.0000],
 [    1.0000,    1.0000,    1.0000]]

1. 全是指定值的矩阵：valueArrayOf

// 创建2行3列的全是指定值的矩阵
INDArray indArray2 = Nd4j.valueArrayOf(new int[] {2, 3}, 888);
disp("全是指定值(888)的矩阵", indArray2);

• 执行结果

全是指定值(888)的矩阵
维度 : 2
形状 : [2, 3]
完整矩阵 :
[[  888.0000,  888.0000,  888.0000],
 [  888.0000,  888.0000,  888.0000]]

1. rand：随机矩阵（0到1之间的随机数）

// 创建2行3列的随机矩阵
INDArray indArray2 = Nd4j.rand(2, 3);
disp("随机矩阵", indArray2);

• 执行结果

随机矩阵
维度 : 2
形状 : [2, 3]
完整矩阵 :
[[    0.7236,    0.5159,    0.1908],
 [    0.9458,    0.4413,    0.4173]]

1. 随机高斯分布的矩阵(平均值为0,标准差为1)：randn

// 创建2行3列的随机高斯分布矩阵
INDArray indArray3 = Nd4j.randn(2, 3);
disp("随机高斯分布矩阵", indArray3);

• 执行结果

随机高斯分布矩阵
维度 : 2
形状 : [2, 3]
完整矩阵 :
[[   -0.4287,   -0.5790,    0.5004],
 [   -0.5122,    1.0551,   -0.1998]]

1. 等差数列：linspace

// 创建等差数列，
// 从1到6、长度为10的等差数列
INDArray indArray4 = Nd4j.linspace(1,6, 10);
disp("等差数列", indArray4);

• 执行结果

等差数列
维度 : 1
形状 : [10]
完整矩阵 :
[    1.0000,    1.5556,    2.1111,    2.6667,    3.2222,    3.7778,    4.3333,    4.8889,    5.4444,    6.0000]

1. 根据数组创建矩阵：create(float[] data, int[] shape)

// 根据数组创建2行3列的矩阵
INDArray indArray6 = Nd4j.create(new float[] {1, 2, 3, 4, 5, 6}, new int[]  {2,3});
disp("根据数组创建矩阵", indArray6);

• 执行结果

根据数组创建矩阵
维度 : 2
形状 : [2, 3]
完整矩阵 :
[[    1.0000,    2.0000,    3.0000],
 [    4.0000,    5.0000,    6.0000]]

1. 三维矩阵

// 三维矩阵
INDArray indArray7 = Nd4j.valueArrayOf(new int[] {2, 2, 3}, 888);
disp("三维矩阵", indArray7);
```shell

三维矩阵
维度 : 3
形状 : [2, 2, 3]
完整矩阵 :
[[[  888.0000,  888.0000,  888.0000],
  [  888.0000,  888.0000,  888.0000]], 

 [[  888.0000,  888.0000,  888.0000],
  [  888.0000,  888.0000,  888.0000]]]

1. 创建正方形二维矩阵，并且对角线上的元素值都是1.0：

// 创建3行3列的二维矩阵，对角线值为1.0
INDArray indArray10 = Nd4j.eye(3);
disp("3*3矩阵，且对角线都是1.0", indArray10);

• 执行结果

3*3矩阵，且对角线都是1.0
维度 : 2
形状 : [3, 3]
完整矩阵 :
[[    1.0000,         0,         0],
 [         0,    1.0000,         0],
 [         0,         0,    1.0000]]

读操作

• 接下来试试读取相关的操作，回顾前面用数组创建的2行3列的矩阵，内容如下：

[[    1.0000,    2.0000,    3.0000],
 [    4.0000,    5.0000,    6.0000]]

1. 读取指定位置：

System.out.println("读取第一行第一列位置的值 : " + indArray6.getDouble(1,1));

• 执行结果

读取第一行第一列位置的值 : 5.0

1. 指定行：

System.out.println("读取第一行 : " + indArray6.getRow(1));

• 执行结果

读取第一行 : [    4.0000,    5.0000,    6.0000]

1. 指定列：

System.out.println("读取第二列 : " + indArray6.getColumn(2));

• 执行结果

读取第二列 : [    3.0000,    6.0000]

1. 指定多列：

System.out.println("读取第二、三列 : " + indArray6.getColumns(1,2));

• 执行结果

读取第二、三列 : [[    2.0000,    3.0000],
 [    5.0000,    6.0000]]

写操作

• 接下来试试读取相关的操作，回顾前面用数组创建的2行3列的矩阵，内容如下：

[[    1.0000,    2.0000,    3.0000],
 [    4.0000,    5.0000,    6.0000]]

1. 修改指定位置，查看了源码后发现，put方法内容实际上是在调用putScalar方法：

indArray6.put(1,1, 123);
indArray6.putScalar(0,0, 456);
disp("a. 修改后", indArray6);

• 执行结果

a. 修改后
维度 : 2
形状 : [2, 3]
完整矩阵 :
[[  456.0000,    2.0000,    3.0000],
 [    4.0000,  123.0000,    6.0000]]

1. 修改整行：

// 准备一维数组
INDArray row1 = Nd4j.create(new float[] {9,8,7});

// 用一维数组替换矩阵的整行
indArray6.putRow(1, row1);
disp("b. 修改后", indArray6);

• 执行结果

b. 修改后
维度 : 2
形状 : [2, 3]
完整矩阵 :
[[  456.0000,    2.0000,    3.0000],
 [    9.0000,    8.0000,    7.0000]]

矩阵计算

• 矩阵计算，咱们从最基本的四则运算开始

1. 加减乘除，入参是一个标量，会与矩阵中的所有元素做计算

// 准备好原始数据，2行3列矩阵
indArray6 = Nd4j.create(new float[] {1, 2, 3, 4, 5, 6}, new int[]  {2,3});

// 加法
disp("加法", indArray6.add(1));

// 减法
disp("减法", indArray6.sub(1));

// 乘法
disp("乘法", indArray6.mul(2));

// 除法
disp("除法", indArray6.div(2));

• 执行结果

加法
维度 : 2
形状 : [2, 3]
完整矩阵 :
[[    2.0000,    3.0000,    4.0000],
 [    5.0000,    6.0000,    7.0000]]
*****************************************************
减法
维度 : 2
形状 : [2, 3]
完整矩阵 :
[[         0,    1.0000,    2.0000],
 [    3.0000,    4.0000,    5.0000]]
*****************************************************
乘法
维度 : 2
形状 : [2, 3]
完整矩阵 :
[[    2.0000,    4.0000,    6.0000],
 [    8.0000,   10.0000,   12.0000]]
*****************************************************
除法
维度 : 2
形状 : [2, 3]
完整矩阵 :
[[    0.5000,    1.0000,    1.5000],
 [    2.0000,    2.5000,    3.0000]]

1. 前面的add方法，执行完毕后会生成一个新的NDArray实例，不影响原对象，但如果调用的是addi，就会修改原对象的内容：

INDArray indArray8 = Nd4j.create(new float[] {1, 2, 3, 4, 5, 6}, new int[]  {2,3});
disp("替换前", indArray8);
indArray8.addi(1);
disp("替换后", indArray8);

• 执行结果

替换前
维度 : 2
形状 : [2, 3]
完整矩阵 :
[[    1.0000,    2.0000,    3.0000],
 [    4.0000,    5.0000,    6.0000]]
*****************************************************
替换后
维度 : 2
形状 : [2, 3]
完整矩阵 :
[[    2.0000,    3.0000,    4.0000],
 [    5.0000,    6.0000,    7.0000]]

1. 展开：Nd4j.toFlattened，2行3列的二维矩阵展开后成了一维的

disp("展开", Nd4j.toFlattened(indArray6));

• 执行结果

展开
维度 : 1
形状 : [6]
完整矩阵 :
[    1.0000,    2.0000,    3.0000,    4.0000,    5.0000,    6.0000]

1. 转换：reshape，相当于使用原有数据，但是换一个shape入参

disp("转换", indArray6.reshape(3,2));

• 执行结果

转换
维度 : 2
形状 : [3, 2]
完整矩阵 :
[[    1.0000,    2.0000],
 [    3.0000,    4.0000],
 [    5.0000,    6.0000]]

1. 提取正方形矩阵的对角线：diag，得到的结果是一维的

// 创建一个人3行3列的正方形矩阵
INDArray indArray9 = Nd4j.create(new float[] {1, 2, 3, 4, 5, 6, 7, 8, 9}, new int[]  {3,3});
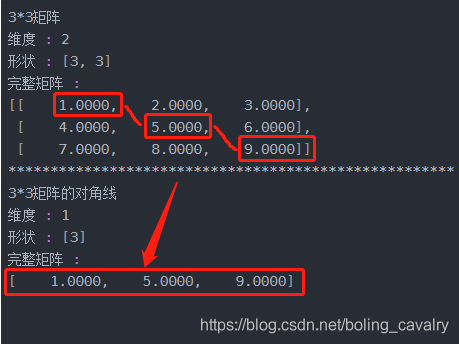
disp("3*3矩阵", indArray9);
// 提取正方形矩阵的对角线
disp("3*3矩阵的对角线", Nd4j.diag(indArray9));

• 执行结果如下图，diag方法得到了源对象的对角线

1. 基于源矩阵形状创建新矩阵，且值都相通（入参值），然后用此新矩阵减去源矩阵：rsub

// 初始化一个2行3列的矩阵
INDArray indArray11 = Nd4j.create(new float[] {1, 2, 3, 4, 5, 6}, new int[]  {2,3});
// 参考indArray12的结构创建一个2行3列的矩阵，该矩阵的所有元素的值都等于10(入参)，
// 然后，用该矩阵减去indArray11，结果作为rsub方法的返回值返回
INDArray indArray12 = indArray11.rsub(10);
disp("rsub方法", indArray12);

• 执行结果如下，可见所有值都是10减去源矩阵对应位置的值：

rsub方法
维度 : 2
形状 : [2, 3]
完整矩阵 :
[[    9.0000,    8.0000,    7.0000],
 [    6.0000,    5.0000,    4.0000]]

1. 两个矩阵相加：add，两个形状相通的矩阵，同样位置的值相加：

INDArray indArray13 = Nd4j.create(new float[] {1, 2, 3, 4, 5, 6}, new int[]  {2,3});
INDArray indArray14 = Nd4j.create(new float[] {1, 1, 1, 1, 1, 1}, new int[]  {2,3});

disp("矩阵相加", indArray13.add(indArray14));

• 执行结果

矩阵相加
维度 : 2
形状 : [2, 3]
完整矩阵 :
[[    2.0000,    3.0000,    4.0000],
 [    5.0000,    6.0000,    7.0000]]

1. 叉乘：mmul，2行3列乘以3行2列，

INDArray indArray13 = Nd4j.create(new float[] {1, 2, 3, 4, 5, 6}, new int[]  {2,3});
INDArray indArray15 = Nd4j.create(new float[] {1, 2, 3, 4, 5, 6}, new int[]  {3,2});
disp("2行3列", indArray13);
disp("3行2列", indArray15);
disp("2行3列矩阵与3行2列矩阵的叉乘", indArray13.mmul(indArray15));

• 执行结果，可见，2行3列矩阵的每一行的元素，都和3行2列矩阵每一列的元素做两两相乘再相加，一共四个值，所以结果就是2行2列的矩阵：

1. 矩阵所有元素值累加：sum

INDArray indArray16 = Nd4j.create(new float[] {1, 2, 3, 4, 5, 6}, new int[]  {2,3});
// 总和
double sum = indArray16.sum().getDouble();
System.out.println("矩阵元素累加和 : " + sum);

• 执行结果

矩阵元素累加和 : 21.0

1. 转置操作（不改变源对象）：transpose

INDArray indArray16 = Nd4j.create(new float[] {1, 2, 3, 4, 5, 6}, new int[]  {2,3});

disp("转置前", indArray16);
disp("转置操作", indArray16.transpose());
disp("transpose操作后的原值(不变)", indArray16);

• 执行结果，可见2行3列转置后变成了3行2列，但是生成了新对象，而源对象未改变

转置前
维度 : 2
形状 : [2, 3]
完整矩阵 :
[[    1.0000,    2.0000,    3.0000],
 [    4.0000,    5.0000,    6.0000]]
*****************************************************
转置操作
维度 : 2
形状 : [3, 2]
完整矩阵 :
[[    1.0000,    4.0000],
 [    2.0000,    5.0000],
 [    3.0000,    6.0000]]
*****************************************************
transpose操作后的原值(不变)
维度 : 2
形状 : [2, 3]
完整矩阵 :
[[    1.0000,    2.0000,    3.0000],
 [    4.0000,    5.0000,    6.0000]]

1. 转置操作（源对象被改变）：transposei

INDArray indArray16 = Nd4j.create(new float[] {1, 2, 3, 4, 5, 6}, new int[]  {2,3});
disp("转置前", indArray16);
disp("转置操作", indArray16.transposei());
disp("transposei操作后的原值(已变)", indArray16);

• 执行结果

转置前
维度 : 2
形状 : [2, 3]
完整矩阵 :
[[    1.0000,    2.0000,    3.0000],
 [    4.0000,    5.0000,    6.0000]]
*****************************************************
转置操作
维度 : 2
形状 : [3, 2]
完整矩阵 :
[[    1.0000,    4.0000],
 [    2.0000,    5.0000],
 [    3.0000,    6.0000]]
*****************************************************
transposei操作后的原值(已变)
维度 : 2
形状 : [3, 2]
完整矩阵 :
[[    1.0000,    4.0000],
 [    2.0000,    5.0000],
 [    3.0000,    6.0000]]

1. 横向拼接：hstack，要求两个矩阵行数相等

// 2行3列
INDArray indArray17 = Nd4j.create(new float[] {1, 2, 3, 4, 5, 6}, new int[]  {2,3});
// 2行1列
INDArray indArray18 = Nd4j.create(new float[] {1, 2}, new int[]  {2,1});
disp("源矩阵", indArray17);
disp("拼接上的矩阵", indArray18);
// 2行3列的矩阵，横向拼接一列后，变成了2行4列
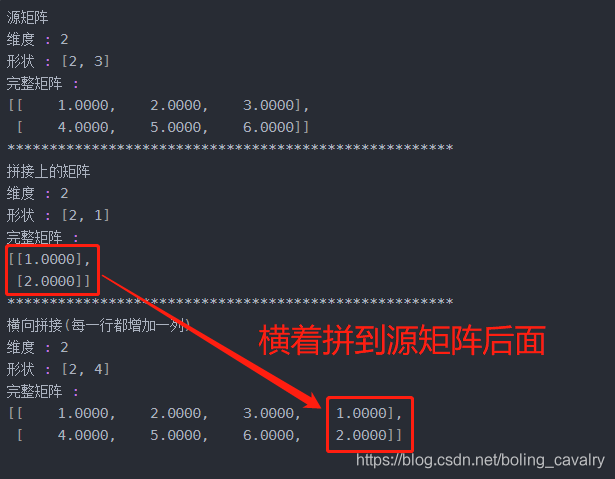
disp("横向拼接(每一行都增加一列)", Nd4j.hstack(indArray17, indArray18));

• 执行结果如下图，可见是把indArray18 横着拼到indArray17 的右侧

1. 纵向拼接：vstack，要求两个矩阵列数相等

// 2行3列
INDArray indArray19 = Nd4j.create(new float[] {1, 2, 3, 4, 5, 6}, new int[]  {2,3});
// 1行3列
INDArray indArray20 = Nd4j.create(new float[] {1, 2, 3}, new int[]  {1,3});
disp("源矩阵", indArray17);
disp("拼接上的矩阵", indArray18);
// 2行3列的矩阵，纵向拼接一行，变成了3行3列
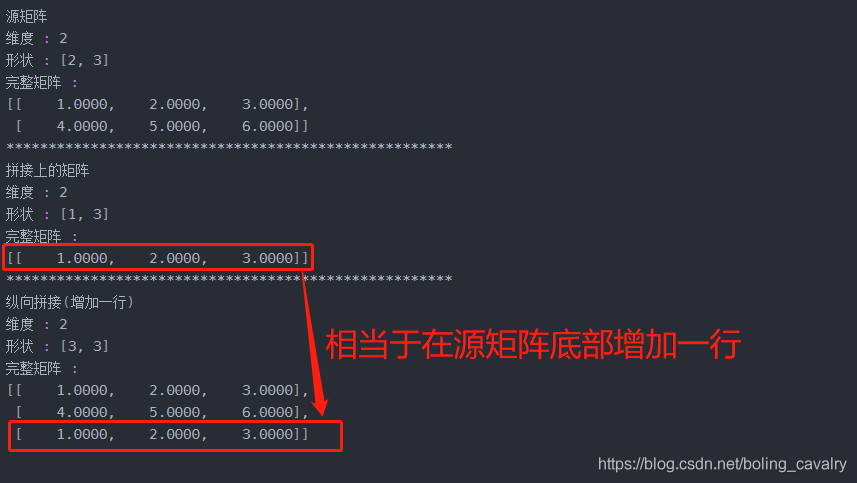
disp("纵向拼接(增加一行)", Nd4j.vstack(indArray19, indArray20));

• 执行结果如下图，可见是把indArray20放在了indArray19的底部

• 以上就是矩阵操作的常用API了，希望能给您一些参考，在深度学习的开发中更熟练的操作数据

你不孤单，欣宸原创一路相伴

1. Java系列
2. Spring系列
3. Docker系列
4. kubernetes系列
5. 数据库+中间件系列
6. DevOps系列

欢迎关注公众号：程序员欣宸

微信搜索「程序员欣宸」，我是欣宸，期待与您一同畅游Java世界...

https://github.com/zq2599/blog_demos