Note -「多项式」基础模板(FFT/NTT/多模 NTT)光速入门
进阶篇戳这里。
\(\omega\) 何为「多项式」\(\omega\)
多项式(polynomial)是指由变量(variable)、系数(coefficient)以及它们之间的加、减、乘、幂运算(非负整数次方)得到的表达式。多项式就是整式。
\(\omega\) 基本概念 \(\omega\)
在初中阶段就有所接触:整式可以包含加、减、乘、除、乘方五种对变量的运算,同时要求除数不含有变量。设 \(x,y\) 为变量,其余字母为常量,则 \(xy,a+by\) 是整式,\(\sqrt{a}x+\pi y~(a\ge0)\) 也是整式,因为根号下的 \(a\) 是常量;\(\frac{x}y,\sqrt{xy}\) 则不是整式。
在本文中,我们所说的多项式通常指一元多项式,即仅含一个变量 \(x\) 的多项式。并简记一个多项式 \(A(x)=a_0+a_1x+a_2x^2+\cdots+a_nx^n\),其中 \(n\) 是 \(A(x)\) 的次数。
\(\omega\) 系数表示法 & 点值表示法 \(\omega\)
在上文中 \(A(x)=a_0+a_1x+a_2x^2+\cdots+a_nx^n\) 就是多项式的系数表示法。而可以证明,对于一个 \(n\) 次多项式,可以用任意 \(n+1\) 个其函数图像上不重合的点来唯一确定这个多项式。我们任取 \(n+1\) 个横坐标的值 \(x_0,x_1,\dots,x_n\),代入 \(A(x)\),求得 \(n+1\) 个点 \((x_0,y_0),(x_1,y_1),\dots,(x_n,y_n)\),就可以用这 \(n+1\) 个点唯一确定 \(A(x)\),这也被称为 \(A(x)\) 的点值表示法。注意到 \(x\) 是任意的,所以同一个多项式的点值表示法不唯一。
接下来,抛出我们的问题:设有两个多项式 \(A(x),B(x)\),如何计算它们的乘积(亦称作卷积) \(C(x)=A(x)\cdot B(x)\) 呢?
一个简单的想法,我们可以利用乘法分配律求到 \(C(x)\) 每一项的系数。于是:
\]
注意求和中的 \(+\infty\) 只是一种形式记法,事实上,当 \(i\) 大于 \(A(x)\) 的次数与 \(B(x)\) 的次数之和时,\(x^i\) 的系数 \(c_i\) 显然为 \(0\)。
不过呢……从算法设计的角度,这种求多项式乘法的方式的复杂度是 \(\mathcal{O}(n^2)\) 的,好慢 qwq。
联系到点值表示法,如果对于同一个横坐标 \(x\),其在 \(A(x)\) 上的坐标为 \((x,y_a)\),在 \(B(x)\) 上的坐标为 \((x,y_b)\),那么代入最初的表达式,它在 \(C(x)=A(x)\cdot B(x)\) 上的坐标就是 \((x,y_ay_b)\) 呐。所以,在已知 \(A(x)\) 和 \(B(x)\) 的点值表示法时,我们可以用 \(\mathcal{O}(n)\) 的时间求出 \(C(x)\) 的点值表示法!
\(\omega\) 傅里叶(Fourier)变换 \(\omega\)
我们继续解决上文多项式乘法的问题——找到一个高效的算法,实现系数与点值表示法的转换。
本节中,若非特别说明,\(n=2^k,k\in\mathbb{N}\)。
\(\omega\) 概述 \(\omega\)
离散傅里叶变换(Discrete Fourier Transform,DFT),是傅里叶变换在时域和频域上都呈离散的形式,将信号的时域采样变换为其 DTFT 的频域采样。
FFT 是一种高效实现 DFT 的算法,称为快速傅立叶变换(Fast Fourier Transform,FFT)。它对傅里叶变换的理论并没有新的发现,但是对于在计算机系统或者说数字系统中应用离散傅立叶变换,可以说是进了一大步。
\(\omega\) 前置知识 - 复数 \(\omega\)
其实很简单:我们把形如 \(z=a+bi\) 的数称为复数,其中 \(a,b\in\mathbb R\); \(a\) 为实部,\(b\) 为虚部,\(i\) 有 \(i^2=-1\),为虚数单位。我们可以把复数与二维平面上的向量 \((a,b)\) 一一对应,此时 \(x\) 轴称为实轴,\(y\) 轴称为虚轴。并记其与 \(x\) 轴正方向的夹角为辐角 \(\theta\),向量的模长为 \(|z|\)。如图,对于 \(z=3+2i\):
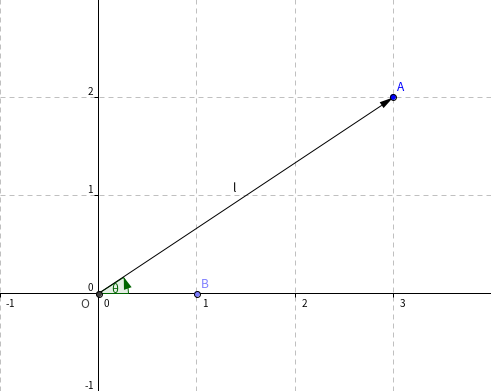
其中 \(l\) 为模长,\(\theta\) 为辐角。接下来我们研究复数的一些基本运算:
加减法:\(z_1\pm z_2=(a_1\pm a_2)+(b_1\pm b_2)i\)。
乘法:\(z_1z_2=(a_1a_2-b_1b_2)+(a_1b_2+a_2b_1)i\)。
进一步研究,发现:
\[|z_1z_2|^2=(a_1^2a_2^2-2a_1a_2b_1b_2+b_1^2b_2^2)+(a_1^2b_2^2+2a_1a_2b_1b_2+a_2^2b_1^2)=(a_1^2+b_1^2)(a_2^2+b_2^2)
\]最后一步用了简单的因式分解技巧。由于 \(a_1^2+b_1^2=|z_1|^2,a_2^2+b_2^2=|z_2|^2\),所以有 \(|z_1z_2|=|z_1||z_2|\)。
此外,运用 \(\tan\) 的和角公式,还可以求到 \(\theta_{z_1z_2}=\theta_{z_1}+\theta_{z_2}\)。
所以,复数的乘法有一个重要的几何意义:模长相乘,辐角相加。
最后,我们定义 \(\overline{z}\) 为 \(z\) 关于 \(x\) 轴对称的向量,称为 \(z\) 的共轭复数。即若 \(z=a+bi\),有 \(\overline{z}=a-bi\)。可以发现 \(z\cdot\overline{z}=a^2+b^2\in\mathbb R\)。 为后文方便叙述,记 \(\operatorname{conj}(z)=\overline z\)。
\(\omega\) 单位根 \(\omega\)
定义 \(n\) 次单位根为所有满足 \(z^n=1\) 的 \(z\)。根据乘法的几何意义,可知 \(|z|=1\),\(n\theta_z=2k\pi\),其中 \(k\in\mathbb{Z}\)。于是满足条件且小于 \(2\pi\) 的 \(\theta_z\) 集合为 \(\{0,\frac{1\times2\pi}{n},\frac{2\times2\pi}{n},\dots,\frac{(n-1)\times2\pi}{n}\}\),共 \(n\) 个。我们记 \(\omega_n^k\) (\(\omega\),/'əʊmɪɡə/)为第 \(k\) 个 \(n\) 次单位根(\(k=0,1,\dots,n-1\))。如图,当 \(n=8\) 时:
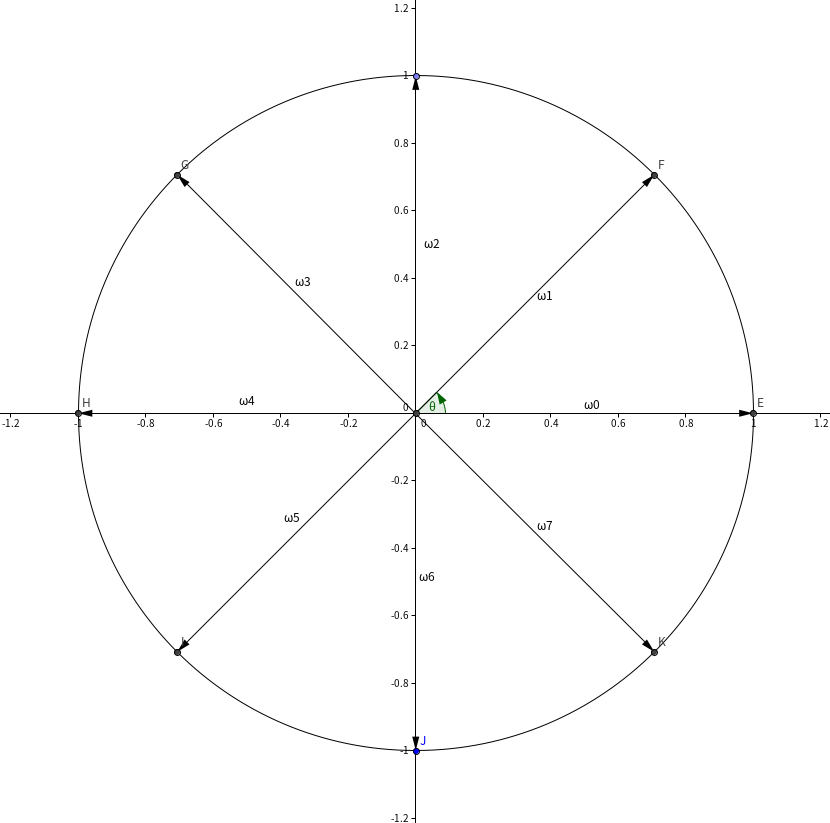
运用简单的三角函数知识,得到:
\]
可以发现,单位根实际上体现了一个周期意义:\(\omega_n^n=\omega_n^0\)。所以此后单位根的上标(乘方或是编号,它们在运算意义上等价)默认对单位根次数取模。单位根有如下性质:
- \(\omega_n^j\omega_n^k=\omega_n^{j+k}\)。
- \(\omega_{kn}^{kj}=\omega_n^j\)。
- \(\omega_{2n}^k=-\omega_{2n}^{k+n}\)。
可以结合乘法几何意义与公式理解。
\(\omega\) 快速傅里叶正变换(FFT)\(\omega\)
有必要重申我们的目标:实现系数与点值表示法的转换。
现在,设有 \(A(x)=a_0+a_1x+a_2x^2+\cdots+a_{n-1}x^{n-1}\),我们希望代入 \(n\) 次单位根 \(\omega_n^0,\omega_n^1,\dots,\omega_n^{n-1}\) 这 \(n\) 个复数来取得 \(A(x)\) 的点值表示法。
分开奇数项与偶数项,记:
\]
\]
利用 \(A_e(x)\) 和 \(A_o(x)\) 来表示 \(A(x)\),有:
\]
设 \(n=2m\),尝试代入一个 \(\omega_n^k\):
\]
注意到 \(\omega_n^{2k}=\omega_{2m}^{2k}=\omega_m^k\),所以:
\]
类似地,代入 \(\omega_n^{k+m}=-\omega_n^k\),有:
\]
所以,当已知 \(A_e(\omega_m^k)\) 和 \(A_o(\omega_m^k)\) 时,可以 \(\mathcal{O}(1)\) 计算出 \(A(\omega_n^k)\) 和 \(A(\omega_n^{k+m})\)。现在,就有了一个算法雏形:
Function name: FFT.
Input: a polynomial \(A(x)=a_0+a_1x_1+\cdots\) which's length is \(n~(n=2^k,k\in\mathbb N)\).
Output: a set \(\mathcal A=\{A(\omega_n^0),A(\omega_n^1),\dots,A(\omega_n^{n-1})\}\).
if \(n=1\) then
return \(\{(a_0,0)\}\)
\(m\leftarrow\frac{n}2\)
\(A_e(x)\leftarrow\sum_{i\in[0,n)\land2|i}a_ix^{\frac{i}2}\)
\(A_o(x)\leftarrow\sum_{i\in[0,n)\land2\not|i}a_ix^{\frac{i-1}2}\)
\(\mathcal A\leftarrow\varnothing\)
\(\mathcal{A}_e\leftarrow\operatorname{FFT}(A_e,m)\)
\(\mathcal{A}_o\leftarrow\operatorname{FFT}(A_o,m)\)
\(k\leftarrow0\)
while \(k<m\) do
\(\mathcal{A}_k\leftarrow{\mathcal{A}_e}_k+\omega_n^k{\mathcal{A}_o}_k\)
\(\mathcal{A}_{k+m}\leftarrow{\mathcal{A}_e}_k-\omega_n^k{\mathcal{A}_o}_k\)
\(k\leftarrow k+1\)
return \(\mathcal A\)
复杂度是 \(\mathcal{T}(n)=2\mathcal{T}(\frac{n}2)+\mathcal{O}(n)=\mathcal{O}(n\log n)\)。在后文中,“多项式 \(A(x)\) 的点值表示”均指由上述 FFT 算法得到的 \(\mathcal A\)。
别着急做题,这种实现方法 SPFA 了 qwq。
\(\omega\) 快速傅里叶逆变换(IFFT)\(\omega\)
利用 FFT,我们可以快速地将系数表示法转换成点值表示法,那怎么在同样优秀的复杂度内转回去呢?
从本质入手,考虑到 \(\mathcal A_j=\sum_{k=0}^{n-1}a_k(\omega_n^j)^k\),我们把它写成矩阵乘法的形式:
(\omega_n^0)^0&(\omega_n^0)^1&\cdots&(\omega_n^0)^{n-1}\\
(\omega_n^1)^0&(\omega_n^1)^0&\cdots&(\omega_n^1)^{n-1}\\
\vdots&\vdots&\ddots&\vdots\\
(\omega_n^{n-1})^0&(\omega_n^{n-1})^1&\cdots&(\omega_n^{n-1})^{n-1}
\end{bmatrix}
\begin{bmatrix}
a_0\\a_1\\\vdots\\a_{n-1}
\end{bmatrix}=
\begin{bmatrix}
\mathcal A_0\\
\mathcal A_1\\
\vdots\\
\mathcal A_{n-1}
\end{bmatrix}
\]
令左侧的系数矩阵为 \(U\),考虑系数矩阵 \(V\):
(\omega_n^{-0})^0&(\omega_n^{-0})^1&\cdots&(\omega_n^{-0})^{n-1}\\
(\omega_n^{-1})^0&(\omega_n^{-1})^0&\cdots&(\omega_n^{-1})^{n-1}\\
\vdots&\vdots&\ddots&\vdots\\
(\omega_n^{-(n-1)})^0&(\omega_n^{-(n-1)})^1&\cdots&(\omega_n^{-(n-1)})^{n-1}
\end{bmatrix}
\]
那么:
\]
当 \(i=j\) 时,显然 \((U\cdot V)_{ij}=n\)。
当 \(i\not=j\) 时,发现是等比数列的形式。所以 \((U\cdot V)_{ij}=\frac{1-\omega_n^{n(j-i)}}{1-\omega_n^{j-i}}\)。又因为 \(\omega_n^n=\omega_n^0=1\),所以分子有 \(1-1=0\),则原式 \(=0\)。
综上,\((U\cdot V)_{ij}=[i=j]n\),即 \(\frac{1}nV=U^{-1}\)。
以此,就有:
a_0\\a_1\\\vdots\\a_{n-1}
\end{bmatrix}=\frac{1}{n}V\begin{bmatrix}
\mathcal A_0\\
\mathcal A_1\\
\vdots\\
\mathcal A_{n-1}
\end{bmatrix}=
\frac{1}n\begin{bmatrix}
(\omega_n^{-0})^0&(\omega_n^{-0})^1&\cdots&(\omega_n^{-0})^{n-1}\\
(\omega_n^{-1})^0&(\omega_n^{-1})^0&\cdots&(\omega_n^{-1})^{n-1}\\
\vdots&\vdots&\ddots&\vdots\\
(\omega_n^{-(n-1)})^0&(\omega_n^{-(n-1)})^1&\cdots&(\omega_n^{-(n-1)})^{n-1}
\end{bmatrix}
\begin{bmatrix}
\mathcal A_0\\
\mathcal A_1\\
\vdots\\
\mathcal A_{n-1}
\end{bmatrix}
\]
注意到 \(\omega_n^{-k}=\omega_n^{n-k}\),所以依然能够用 FFT 的递归形式求解。
\(\omega\) 迭代实现 \(\omega\)
常数惊人呐……
这里,我们将尝试把递归的 FFT Fast-Fast TLE 转换为仅用循环迭代的 FFT。
观察递归时各系数的位置:
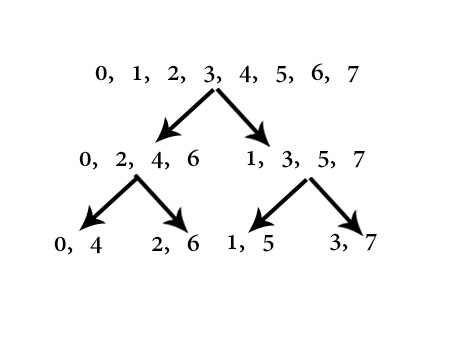
观察第一层和最后一层:
| 原序列 dec | \(0\) | \(1\) | \(2\) | \(3\) | \(4\) | \(5\) | \(6\) | \(7\) |
|---|---|---|---|---|---|---|---|---|
| 原序列 bin | \(000\) | \(001\) | \(010\) | \(011\) | \(100\) | \(101\) | \(110\) | \(111\) |
| 新序列 dec | \(0\) | \(4\) | \(2\) | \(6\) | \(1\) | \(5\) | \(3\) | \(7\) |
| 新序列 bin | \(000\) | \(100\) | \(010\) | \(110\) | \(001\) | \(101\) | \(011\) | \(111\) |
发现原序列下标的二进制翻转过来就是新序列下标。
所以我们可以先安排好新序列下标,再从下往上迭代就可以了。
\(\omega\) 例题 \(\omega\)
\(\omega\)「洛谷 P3803」「模板」多项式乘法(FFT)\(\omega\)
\(\omega\) 题意简述 \(\omega\)
link.
给两个多项式的每项系数,求其相乘得到的多项式的每项系数。
\(\omega\) 数据规模 \(\omega\)
多项式长度 \(n,m\le10^6\)。
\(\omega\) \(\text{Solution}\) \(\omega\)
直接给出完整代码,建议先模仿实现,以免常数惊人 owo。
不过我不知道怎么折叠显示代码,影响阅读很抱歉 qwq。
\(\omega\) \(\text{Code}\) \(\omega\)
#include <cmath>
#include <cstdio>
#include <iostream>
inline int rint () {
int x = 0, f = 1; char s = getchar ();
for ( ; s < '0' || '9' < s; s = getchar () ) f = s == '-' ? -f : f;
for ( ; '0' <= s && s <= '9'; s = getchar () ) x = x * 10 + ( s ^ '0' );
return x * f;
}
template<typename Tp>
inline void wint ( Tp x ) {
if ( x < 0 ) putchar ( '-' ), x = -x;
if ( 9 < x ) wint ( x / 10 );
putchar ( x % 10 ^ '0' );
}
const int MAXL = 1 << 21;
const double PI = acos ( -1 );
int n, m, rev[MAXL + 5];
struct Complex { // 复数结构体。
double x, y;
Complex () {} Complex ( const double tx, const double ty ): x ( tx ), y ( ty ) {}
inline Complex operator + ( const Complex t ) const { return Complex ( x + t.x, y + t.y ); }
inline Complex operator - ( const Complex t ) const { return Complex ( x - t.x, y - t.y ); }
inline Complex operator * ( const Complex t ) const { return Complex ( x * t.x - y * t.y, x * t.y + y * t.x ); }
inline Complex operator / ( const double t ) const { return Complex ( x / t, y / t ); }
} A[MAXL + 5], B[MAXL + 5];
inline void FFT ( const int n, Complex* A, const int tp ) {
// n为多项式长度,保证是2的整数幂;A为每项系数;tp=1表示正变换,tp=-1表示逆变换。
for ( int i = 0; i < n; ++ i ) if ( i < rev[i] ) std :: swap ( A[i], A[rev[i]] ); // 安排系数位置。
for ( int i = 2, stp = 1; i <= n; i <<= 1, stp <<= 1 ) {
Complex w ( cos ( PI / stp ), tp * sin ( PI / stp ) ); // 当前正在处理$\omega_i$。
for ( int j = 0; j < n; j += i ) {
Complex r ( 1, 0 );
for ( int k = 0; k < stp; ++ k, r = r * w ) {
// $r=\omega_i^k$。
Complex ev ( A[j + k] ), ov ( r * A[j + k + stp] );
A[j + k] = ev + ov, A[j + k + stp] = ev - ov;
}
}
}
if ( ! ~ tp ) for ( int i = 0; i < n; ++ i ) A[i] = A[i] / n; // 逆变换,最后每项/n。
}
inline void ployConv ( const int n, const int m, const Complex* A, const Complex* B, Complex* C ) {
// 计算A(x)与B(x)的卷积,答案为C(x)。
int lg = 0, len = 1;
static Complex tmpA[MAXL + 5], tmpB[MAXL + 5];
for ( ; len < n + m - 1; len <<= 1, ++ lg ); // C(x)长度为n+m-1,找到适合的长度len。
for ( int i = 0; i < len; ++ i ) {
tmpA[i] = A[i], tmpB[i] = B[i];
rev[i] = ( rev[i >> 1] >> 1 ) | ( ( i & 1 ) << lg >> 1 ); // rev[i]为i翻转后的位置,自行理解。
}
FFT ( len, tmpA, 1 ), FFT ( len, tmpB, 1 ); // 正变换求到点值表示。
for ( int i = 0; i < len; ++ i ) C[i] = tmpA[i] * tmpB[i]; // 求到C(x)的点值表示。
FFT ( len, C, -1 ); // 逆变换求到C(x)。
}
int main () {
n = rint () + 1, m = rint () + 1; // 注意这里要+1。
for ( int i = 0; i < n; ++ i ) A[i].x = rint ();
for ( int i = 0; i < m; ++ i ) B[i].x = rint ();
ployConv ( n, m, A, B, A );
for ( int i = 0; i < n + m - 1; ++ i ) {
wint ( ( int ) round ( A[i].x ) );
putchar ( i == n + m - 2 ? '\n' : ' ' );
}
return 0;
}
\(\omega\) 快速数论变换(NTT)\(\omega\)
事实上,由于 FFT 存在大量浮点数运算,其精度和常数都不尽人意。那么能否在整数域下找到单位根的替代品呢?
我们来总结一下单位根应具有的性质:
- \(\omega_n^j\omega_n^k=\omega_n^{j+k}\),注意这里的上标就意义上来说不是乘方,而是编号(当然运算上就是乘方 www)。
- \(\omega_{kn}^{kj}=\omega_n^j\),我们需要这个性质进行递归处理。
- \(\omega_{2n}^k=-\omega_{2n}^{k+n}\),这一性质体现在了合并计算的步骤。
- \((\forall j\not=k)(\omega_n^j\not=\omega_n^k)\),它保证了点值表示法的坐标不重合。
- \(\omega_n^0=1\),它保证了逆变换顺利进行。
考虑在模意义下……
\(\omega\) 原根 \(\omega\)
OI-Wiki 讲得好高深 qwq……
对于素数 \(p\),定义其原根 \(g\) 为满足 \((\forall j,k\in[0,p-1),j\not=k)\left(g^j\not\equiv g^k\pmod p\right)\) 的数。模仿 \(\omega\) 的定义,我们令 \(\alpha_n^k=(g^\frac{p-1}n)^k\)(这里 \(\alpha\) 是随便取的名字 www),考虑其是否满足上述几条性质:
- \(\alpha_n^j\alpha_n^k\equiv\alpha_n^{jk}\pmod p\),乘方性质,显然。
- \(\alpha_{kn}^{kj}=(g^\frac{p-1}{kn})^{kj}=(g^\frac{p-1}n)^j=\alpha_n^j\),成立。
- \(-\alpha_{2n}^{k+n}=-g^\frac{(p-1)(k+n)}{2n}=(-g^\frac{p-1}2)g^\frac{(p-1)k}{2n}\equiv g^\frac{(p-1)k}{2n}=\alpha_{2n}^k\pmod p\)。注意因为 \((g^\frac{p-1}{2})^2\equiv1\pmod p\) 且根据 \(g\) 的定义, \(g^\frac{p-1}2=\alpha_{2n}^n\not=\alpha_{2n}^0\land\alpha_{2n}^0\equiv1\pmod p\),所以 \(g^\frac{p-1}2\equiv-1\pmod p\),等式成立。
- 由定义,成立。
- 显然 \(g\not=0\),成立。
于是,把 FFT 中的所有 \(\omega_n^k\) 替换为 \(\alpha_n^k\) 就变成 NTT 啦!记得取模 owo。
\(\omega\) 实现 \(\omega\)
inline void NTT ( const int n, int* A, const int tp ) {
for ( int i = 0; i < n; ++ i ) if ( i < rev[i] ) A[i] ^= A[rev[i]] ^= A[i] ^= A[rev[i]];
for ( int i = 2, stp = 1, w; i <= n; i <<= 1, stp <<= 1 ) {
w = qkpow ( G, ( MOD - 1 ) / i );
// G为原根,qkpow(a,b)为a的b次方模MOD的结果。
if ( ! ~ tp ) w = qkpow ( w, MOD - 2 );
for ( int j = 0; j < n; j += i ) {
for ( int r = 1, k = j; k < j + stp; ++ k, r = 1ll * r * w % MOD ) {
int ev = A[k], ov = 1ll * r * A[k + stp] % MOD;
A[k] = ( ev + ov ) % MOD, A[k + stp] = ( ev - ov + MOD ) % MOD;
}
}
}
if ( ! ~ tp ) {
int invn = qkpow ( n, MOD - 2 ); // invn为n的逆元。
for ( int i = 0; i < n; ++ i ) A[i] = 1ll * A[i] * invn % MOD;
}
}
\(\omega\) NTT 模数 \(\omega\)
注意到,\(n\) 的大小是随多项式长度变化的,而我们必须保证 \(n|(p-1)\),所以 \(p-1\) 所含 \(2\) 的因子个数决定了 NTT 能够接受的最大多项式长度。对于素数 \(p\) 的选取自然也有了考究。
记住一点,\(998244353-1=2^{23}\times119\),适合做 NTT 模数,原根为 \(3\);\(10^9+7-1=2\times500000003\),不适合做 NTT 模数。
更多 NTT 模数可见这篇博客。
到此,多项式最最基础的知识就结束啦。
\(\omega\) 奇怪的模数 - 任意模数 NTT \(\omega\)
你 NTT 对模数有要求对吧?出题人就笑了……/xyx
好吧,在不接受 FFT 精度误差的情况下,我们来想想办法应对模数不是 NTT 模数,甚至不是素数的毒瘤题吧!
\(\omega\) 三模 NTT \(\omega\)
我偏要用 NTT 模数 www。
顾名思义,我们任取三个 NTT 模数 \(p_1,p_2,p_3\),分别求出多项式乘积的第 \(k\) 项模 \(p_1,p_2,p_3\) 的结果,然后用中国剩余定理(CRT)解出该项模题目给定模数 \(M\) 的结果就行了。不熟悉 CRT 的读者可以参考这篇博客。
我个人认为不太优美懒,因此没有具体实现。在抱歉之余推荐这篇博客的模板 owo。
\(\omega\) 拆系数 FFT(MTT)\(\omega\)
我偏要用 FFT。
缩写释义:MTT - MaoXiao Theory(?) Transformation。快速毛论变换(雾。
假设多项式 \(A(x)=a_0+a_1x+a_2x^2+\cdots,B(x)=b_0+b_1x+b_2x^2+\cdots\),长度均为 \(n\),给定的模数 \(m\),我们要求它们的卷积 \(R(x)=A(x)\cdot B(x)\)。如果直接 FFT,最大的系数可达到 \(nm^2\) 的级别。我们假定 \(n\le10^5,m\le10^9\),那么这样的精度误差是不被接受的。我们取 \(M=\lceil\sqrt m\rceil\),并定义以下几个多项式:
C(x)&=\sum_{k=0}^{n-1}(a_k\bmod M)x^k\\
D(x)&=\sum_{k=0}^{n-1}\frac{a_k-(a_k\bmod M)}{M}x^k\\
E(x)&=\sum_{k=0}^{n-1}(b_k\bmod M)x^k\\
F(x)&=\sum_{k=0}^{n-1}\frac{a_k-(a_k\bmod M)}{M}x^k
\end{aligned}
\]
可以发现,以上每个多项式的系数都是不超过 \(M\) 的,那么任意两个多项式卷积的最大系数不超过 \(nM^2\le10^{14}\),在 double 的承受范围以内。(保险起见,建议开 long double,不过对于某些 g++ 版本貌似并没有作用 owo。)我们用这四个多项式表示 \(R(x)\):
\]
这样,在 FFT 过程中,系数大小能被接受;作系数拼凑时步步取模亦能保证不溢出,我们就用 FFT 解决了任意模数 NTT 的问题。一般来说,取 \(M=32768=2^{15}\),可以用位运算节省常数;还应利用 \(\omega_n^k\) 的通项预处理出所有单位根以保障精度。
\(\omega\) 七次转五次 \(\omega\)
数一数,我们对 \(C(x),D(x),E(x),F(x)\) 分别进行了一次 FFT,对 \(D(x)F(x),\) \(C(x)F(x)+D(x)E(x),\) \(C(x)E(x)\) 分别进行了一次 IFFT,一共有七次变换操作,常数有点点大 qwq。
接下来,我们假设有实系数多项式 \(A(x)=a_0+a_1x+a_2x^2+\cdots,B(x)=b_0+b_1x+b_2x^2+\cdots\),长度均为 \(n~(n=2^k,k\in\mathbb N)\),我们希望分别求到它们的点值表示 \(\mathcal A\) 和 \(\mathcal B\)。于是定义:
\]
\]
其中 \(i\) 是虚数单位。设 \(P\) 与 \(Q\) 的点值表示分别为 \(\mathcal P,\mathcal Q\),并记 \(\omega_n^k\) 的辐角 \(\frac{2\pi k}n\) 为 \(\theta_n^k\)。那么:
\mathcal P_k&=A(\omega_n^k)+iB(\omega_n^k)\\
&=\sum_{j=0}^{n-1}a_j\omega_n^k+ib_j\omega_n^k\\
&=\sum_{j=0}^{n-1}(a_j+ib_j)(\cos\theta_n^k+i\sin\theta_n^k)\\\\
\mathcal Q_k&=A(\omega_n^k)-iB(\omega_n^k)\\
&=\sum_{j=0}^{n-1}a_j\omega_n^{jk}-ib_j\omega_n^{jk}\\
&=\sum_{j=0}^{n-1}(a_j-ib_j)(\cos\theta_n^{jk}+i\sin\theta_n^{jk})\\
&=\sum_{j=0}^{n-1}(a_j\cos\theta_n^{jk}+b_j\sin\theta_n^{jk})+i(a_j\sin\theta_n^{jk}-b_j\cos\theta_n^{jk})\\
&=\operatorname{conj}\left(\sum_{j=0}^{n-1}(a_j\cos\theta_n^{jk}+b_j\sin\theta_n^{jk})-i(a_j\sin\theta_n^{jk}-b_j\cos\theta_n^{jk})\right)\\
&=\operatorname{conj}\left(\sum_{j=0}^{n-1}\left(a_j\cos(-\theta_n^{jk})-b_j\sin(-\theta_n^{jk})\right)+i\left(a_j\sin(-\theta_n^{jk})-b_j\cos(-\theta_n^{jk})\right)\right)\\
&=\operatorname{conj}\left(\sum_{j=0}^{n-1}(a_j+ib_j)\left(\cos(-\theta_n^{jk})+i\sin(-\theta_n^{jk})\right)\right)\\
&=\operatorname{conj}\left(\sum_{j=0}^{n-1}(a_j+ib_j)\left(\cos\theta_n^{-jk}+i\sin\theta_n^{-jk}\right)\right)\\
&=\operatorname{conj}\left(\sum_{j=0}^{n-1}(a_j+ib_j)\left(\cos\theta_n^{(n-k)j}+i\sin\theta_n^{(n-k)j}\right)\right)\\
&=\operatorname{conj}(\mathcal P_{n-k})
\end{aligned}
\]
推导时,时刻留意 \(\theta_n\) 的上标在模 \(n\) 意义下嗷!
最终,发现 \(\mathcal Q\) 可以在求得 \(\mathcal P\) 的前提下 \(\mathcal O(1)\) 求到。只需要用 \(\mathcal P\) 和 \(\mathcal Q\) 表示出 \(\mathcal A\) 和 \(\mathcal B\):
\mathcal B_k=i\frac{\mathcal Q_k-\mathcal P_k}2
\]
就可以用一次 FFT 求出两个多项式的点值表示啦!(我认为毛啸的论文在 \(\mathcal B_k\) 的表达式处有误,右侧分子应为本文的 \(\mathcal Q_k-\mathcal P_k\) 而非 \(\mathcal P_k-\mathcal Q_k\),欢迎指正 qwq。)
于是,我们可以把对 \(C(x),D(x),E(x),F(x)\) 的 FFT 合并为两组,就只需要五次 FFT 啦!
\(\omega\) 五次转四次 \(\omega\)
正变换已经足够优秀了,我们接下来考虑逆变换的合并。按照上文的推导,我们只需要求到 \(P(x)\) 或者 \(Q(x)\) 就可以了——因为原多项式是实系数的,所以对于 \(P(x)\) 或 \(Q(x)\) 的每一项,我们能够区分出其实部就是 \(A(x)\) 的系数而虚部就是 \(B(x)\) 的系数。既然已知 \(\mathcal A\) 和 \(\mathcal B\),直接利用定义式,有:
\]
逆变换 \(\mathcal P\) 得到 \(P(x)\),就可以把两次逆变换合并为一次了。最终,我们把四次正变换合并为两次,三次逆变换合并为两次,仅用四次 FFT 就解决了这一问题。
\(\omega\) 例题 \(\omega\)
\(\omega\) 「洛谷 P4245」「模板」任意模数 NTT
\(\omega\) 题意简述 \(\omega\)
link.
给两个多项式,求其在模 \(p\) 意义下的卷积。
\(\omega\) 数据规模 \(\omega\)
多项式长度 \(n\le10^5\),系数 \(a_k,b_k\le10^9\),\(p\le10^9+9\)。
\(\omega\) \(\text{Solution}\) \(\omega\)
这里仅给出四次 FFT 的 MTT 做法。
\(\omega\) \(\text{Code}\) \(\omega\)
#include <cmath>
#include <cstdio>
#include <iostream>
typedef long long LL;
inline int rint () { /* 快读 */ }
inline void wint ( const int x ) { /* 快输 */ }
const int MAXN = 1 << 18;
const double PI = acos ( -1 );
int n, m, p, A[MAXN + 5], B[MAXN + 5], rev[MAXN + 5];
struct Complex {
/* 复数结构体 */
} omega[MAXN + 5], P[MAXN + 5], Q[MAXN + 5], C[MAXN + 5], D[MAXN + 5], E[MAXN + 5], F[MAXN + 5];
inline void FFT ( const int n, Complex* A, const int tp ) { /* FFT,应使用预处理好的单位根omega[]。 */ }
int main () {
n = rint () + 1, m = rint () + 1, p = rint ();
for ( int i = 0; i < n; ++ i ) A[i] = rint () % p, P[i] = Complex ( A[i] & 0x7fff, A[i] >> 15 );
for ( int i = 0; i < m; ++ i ) B[i] = rint () % p, Q[i] = Complex ( B[i] & 0x7fff, B[i] >> 15 );
int lg = 0, len = 1;
for ( ; len < n + m - 1; len <<= 1, ++ lg );
for ( int i = 0; i < len; ++ i ) rev[i] = ( rev[i >> 1] >> 1 ) | ( ( i & 1 ) << lg >> 1 );
for ( int i = 1; i < len; i <<= 1 ) { // 预处理单位根。
for ( int k = 0; k < i; ++ k ) {
omega[len / i * k] = Complex ( cos ( PI * k / i ), sin ( PI * k / i ) );
}
}
FFT ( len, P, 1 ), FFT ( len, Q, 1 );
for ( int i = 0; i < len; ++ i ) {
Complex t ( P[( len - i ) % len].x, -P[( len - i ) % len].y );
C[i] = ( P[i] + t ) / 2, D[i] = Complex ( 0, 1 ) * ( t - P[i] ) / 2;
}
for ( int i = 0; i < len; ++ i ) {
Complex t ( Q[( len - i ) % len].x, -Q[( len - i ) % len].y );
E[i] = ( Q[i] + t ) / 2, F[i] = Complex ( 0, 1 ) * ( t - Q[i] ) / 2;
}
for ( int i = 0; i < len; ++ i ) {
Complex c ( C[i] ), d ( D[i] ), e ( E[i] ), f ( F[i] );
C[i] = c * e, D[i] = c * f + d * e, E[i] = d * f;
P[i] = C[i] + Complex ( 0, 1 ) * E[i];
}
FFT ( len, D, -1 ), FFT ( len, P, -1 );
for ( int i = 0; i < n + m - 1; ++ i ) {
int c = ( LL ( P[i].x + 0.5 ) % p + p ) % p, d = ( LL ( D[i].x + 0.5 ) % p + p ) % p, e = ( LL ( P[i].y + 0.5 ) % p + p ) % p;
wint ( ( c + ( 1ll << 15 ) % p * d % p + ( 1ll << 30 ) % p * e % p ) % p );
putchar ( i + 1 == n + m - 1 ? '\n' : ' ' );
}
return 0;
}
\(\omega\) 「CF 623E」Transforming Sequence \(\omega\)
\(\omega\) 题意简述 \(\omega\)
link.
求有多少个长度为 \(n\) 的序列 \(\{a_n\}\),满足 \(a_k\in(0,2^k)\land a_k\not\subseteq\bigcup_{j=1}^{k-1}a_j\)。这里的集合运算把 \(a_k\) 作为了二进制集合。对 \(10^9+7\) 取模。
\(\omega\) 数据规模 \(\omega\)
\(n\le10^{18},k\in[1,3\times10^4]\)。
\(\omega\) \(\text{Solution}\) \(\omega\)
详见我的题解。题意描述略有不同,请自行理解。为什么我的 MTT 有八次变换啊……
专门提起这道题的目的,除了让大家实战运用 MTT 之外,还想让大家感受倍增这种几乎能融入所有 OI 知识点的思想。
本来还有多项式全家桶,但因为太懒所以烂尾咯 qwq。
\(\omega\) 参考资料 \(\omega\)
按在文中第一次借鉴或引用的位置顺序排列:
- 多项式 @百度百科.
- 整式 @百度百科.
- 快速傅里叶变换 @OI-Wiki.
- 多项式乘法 @Tiw_Air_OAO.
- FFT 用到的各种素数 @Miskcoo's Space.
- 中国剩余定理 CRT @yyb.
- 再探快速傅里叶变换 @毛啸.(网上资源)
Note -「多项式」基础模板(FFT/NTT/多模 NTT)光速入门的更多相关文章
- 多项式 之 快速傅里叶变换(FFT)/数论变换(NTT)/常用套路【入门】
原文链接https://www.cnblogs.com/zhouzhendong/p/Fast-Fourier-Transform.html 多项式 之 快速傅里叶变换(FFT)/数论变换(NTT)/ ...
- 「luogu3380」【模板】二逼平衡树(树套树)
「luogu3380」[模板]二逼平衡树(树套树) 传送门 我写的树套树--线段树套平衡树. 线段树上的每一个节点都是一棵 \(\text{FHQ Treap}\) ,然后我们就可以根据平衡树的基本操 ...
- 「luogu3402」【模板】可持久化并查集
「luogu3402」[模板]可持久化并查集 传送门 我们可以用一个可持久化数组来存每个节点的父亲. 单点信息更新和查询就用主席树多花 一个 \(\log\) 的代价来搞. 然后考虑如何合并两个点. ...
- Note -「计算几何」模板
尚未完整测试,务必留意模板 bug! /* Clearink */ #include <cmath> #include <queue> #include <cstdi ...
- 「LuoguP3808」 【模板】AC自动机(简单版)
题目背景 通过套取数据而直接“打表”过题者,是作弊行为,发现即棕名. 这是一道简单的AC自动机模板题. 用于检测正确性以及算法常数. 为了防止卡OJ,在保证正确的基础上只有两组数据,请不要恶意提交. ...
- 「洛谷3338」「ZJOI2014」力【FFT】
题目链接 [BZOJ] [洛谷] 题解 首先我们需要对这个式子进行化简,否则对着这么大一坨东西只能暴力... \[F_i=\sum_{j<i} \frac{q_iq_j}{(i-j)^2}-\s ...
- 「P3385」【模板】负环(spfa
题目描述 暴力枚举/SPFA/Bellman-ford/奇怪的贪心/超神搜索 输入输出格式 输入格式: 第一行一个正整数T表示数据组数,对于每组数据: 第一行两个正整数N M,表示图有N个顶点,M条边 ...
- 「LuoguP3389」【模板】高斯消元法
题目背景 Gauss消元 题目描述 给定一个线性方程组,对其求解 输入输出格式 输入格式: 第一行,一个正整数 nn 第二至 n+1n+1行,每行 n+1n+1 个整数,为a_1, a_2 \cdot ...
- 「LuoguP4180」 【模板】严格次小生成树[BJWC2010](倍增 LCA Kruscal
题目描述 小C最近学了很多最小生成树的算法,Prim算法.Kurskal算法.消圈算法等等.正当小C洋洋得意之时,小P又来泼小C冷水了.小P说,让小C求出一个无向图的次小生成树,而且这个次小生成树还得 ...
随机推荐
- linux VI命令快捷键
ctrl+f 下一页 ctrl+b 上一页 ctrl+u 上半页 ctrl+d 下半页 数字+空格键 根据当前光标移动多少个字母 0键 光标移动到第一个字母,是当前行的 $键 光标移动到最后一个字母 ...
- 刨根问底: Kafka 到底会不会丢数据?
大家好,我是 华仔, 又跟大家见面了. 上一篇作为专题系列的第二篇,从演进的角度带你深度剖析了关于 Kafka 请求处理全流程以及超高并发的网络架构设计的实现细节,今天开启第三篇,我们来聊聊 Kafk ...
- 使用 SourceGenerator 简化 Options 绑定
目录 摘要 Options 绑定 使用 SourceGenerator 简化 如何 Debug SourceGenerator 如何 Format 生成的代码 使用方法 SourceCode & ...
- 扒一扒@Retryable注解,很优雅,有点意思!
你好呀,我是歪歪. 前几天我 Review 代码的时候发现项目里面有一坨逻辑写的非常的不好,一眼望去简直就是丑陋之极. 我都不知道为什么会有这样的代码存在项目里面,于是我看了一眼提交记录准备叫对应的同 ...
- 《剑指offer》面试题65. 不用加减乘除做加法
问题描述 写一个函数,求两个整数之和,要求在函数体内不得使用 "+"."-"."*"."/" 四则运算符号. 示例: 输 ...
- Solon Web 开发,四、请求上下文
Solon Web 开发 一.开始 二.开发知识准备 三.打包与运行 四.请求上下文 五.数据访问.事务与缓存应用 六.过滤器.处理.拦截器 七.视图模板与Mvc注解 八.校验.及定制与扩展 九.跨域 ...
- gin中间request body绑定到不同的结构体中
1. 一般通过调用 c.Request.Body 方法绑定数据,但不能多次调用这个方法. package main import ( "fmt" "github.com/ ...
- 磁盘sda,hda,sda1,并行,串行
1.sd,hd表示硬盘, a表示第一块盘, 1表示硬盘上的第一个分区 2.sd是Serial ATA Disk ,表示硬盘是scsi,SATA串行接口 hd是 hard disk,表示硬盘是IDE(也 ...
- Typora破解
Typora破解 需要python环境,没有的话需要先安装一下 访问 https://github.com/Mas0nShi/typoraCracker.git下载下来破解需要的压缩包并且解压缩 或者 ...
- jsp中获取下拉框的value问题
遇到问题 最近快期末考试了,今天想写一个简单的增删改查项目练练手,可是在刚写增加的时候就出现了问题,"增"一直是最简单的操作,本来自付很快就能写完,可是数据库中对应的下拉框数据一直 ...
