IEEE754浮点数的转换

将十进制数转换为单精度浮点数

如何将十进制数转换为单精度浮点数参考

首先要知道

IEEE浮点标准：V=(-1)^s * M * 2^E

---

1.符号(sign)s决定这个数是负数(s=1)还是正数,0(s=0)。

2.尾数(significand) M是一个二进制小数.

3.阶码(exponent)E对浮点数加权。

其次要知道单精度浮点数一般下是32位，由三段组成，第一段只有一位即s，第二段有8位，如何得到，可以通过公式中2的指数加上127，所得到的数转换成二进制可得，第三段是由转换的二进制小数中小数部分再补0到23位所得

因此5.75转换成二进制得101.11=1.0111 * 10 ^2

s = 0, E = 2 + 127 = 129,E转换成二进制得10000001，小数部分为0111，再补0至23位

最后5.75的单精度浮点数为01000000101110000000000000000000

同理161.875转换成二进制得10100001.111=1.0100001111 * 2 ^ 7

s = 0, E = 7 + 127 = 134,E转换成二进制得10000110，小数部分为0100001111，再补0至23位

最后161.875的单精度浮点数为01000011001000011110000000000000

-0.0234375的绝对值转换成二进制得0.0000011=1.1 * 2 ^ -6

s = 1, E = -6 + 127 = 121,E转换成二进制得01111001,小数部分为1，再补0至23位

最后-0.0234375的单精度浮点数为10111100110000000000000000000000

在python中实现浮点数的转换

码云

验证上述转换是否正确如图

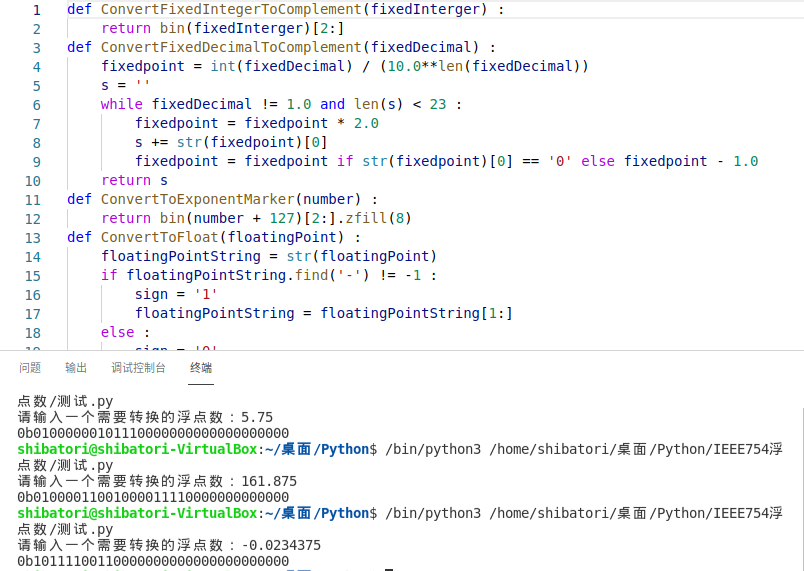
参考网站

1.https://blog.csdn.net/qq_40890756/article/details/83111431

2.https://blog.csdn.net/linda_ds/article/details/78136316

3.http://c.biancheng.net/view/314.html