Noip模拟61 2021.9.25

T1 交通

考场上想了一个$NPC$。应该吧，是要求出图里面的所有可行的不重复欧拉路

无数种做法都无法解出，时间也都耗在这个上面的，于是就考的挺惨的

以后要是觉得当前思路不可做，就试着换一换思路，千万不能在一道题上花费太多时间

正解是一个关系的判断

每一条边选还是不选都会跟另一条边产生连锁关系，那么给他们编上号建边，用并查集判断环就行

然后每个环上选择$n$个不相邻的点，总共$2^{环数}$种方案

 1 #include<bits/stdc++.h>
 2 #define ll long long
 3 using namespace std;
 4 namespace AE86{
 5     inline int read(){
 6         int x=0,f=1;char ch=getchar();
 7         while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
 8         while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}return x*f;
 9     }inline void write(int x,char opt='\n'){
10         char ch[20];int len=0;if(x<0)x=~x+1,putchar('-');
11         do{ch[len++]=x%10+(1<<5)+(1<<4);x/=10;}while(x);
12         for(int i=len-1;i>=0;--i)putchar(ch[i]);putchar(opt);}
13 }using namespace AE86;
14 const int NN=2e5+5,mod=998244353;
15 inline int qmo(int a,int b,int ans=1){
16     int c=mod; while(b){
17         if(b&1) ans=1ll*ans*a%c;
18         b>>=1; a=1ll*a*a%c;
19     } return ans;
20 }
21 struct node{int u,v,id;}p[NN<<1];
22 int n,in[NN<<1][2],ot[NN<<1][2],tot,fa[NN<<1];
23 inline int getfa(int x){return fa[x]=(fa[x]==x?x:getfa(fa[x]));}
24 namespace WSN{
25     inline short main(){
26         freopen("a.in","r",stdin);
27         freopen("a.out","w",stdout);
28         n=read();
29         for(int i=1;i<=n*2;i++) fa[i]=i;
30         for(int i=1;i<=n*2;i++){
31             p[i].u=read(), p[i].v=read();
32             if(in[p[i].v][0]) in[p[i].v][1]=i; else in[p[i].v][0]=i;
33             if(ot[p[i].u][0]) ot[p[i].u][1]=i; else ot[p[i].u][0]=i;
34         }
35         // for(int i=1;i<=n;i++) cout<<in[i][0]<<" "<<in[i][1]<<endl;
36         for(int i=1;i<=n;i++){
37             int X=getfa(in[i][0]),Y=getfa(in[i][1]);
38             if(X==Y) ++tot; else fa[X]=Y;
39             X=getfa(ot[i][0]); Y=getfa(ot[i][1]);
40             if(X==Y) ++tot; else fa[X]=Y;
41         }
42         write(qmo(2,tot));
43         return 0;
44     }
45 }
46 signed main(){return WSN::main();}

T2 小P的单调数列

考虑出一个结论后就非常可做了，就是关于他的价值是取平均，那么分的段越少越好

我们就只比较分成两段的情况和单调上升的情况

然后按照最大权上升子序列处理就好了，写的权值线段树，常数可能会大，可以写两个树状数组

 1 #include<bits/stdc++.h>
 2 #define int long long
 3 using namespace std;
 4 namespace AE86{
 5     inline int read(){
 6         int x=0,f=1;char ch=getchar();
 7         while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
 8         while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}return x*f;
 9     }
10 }using namespace AE86;
11 const int NN=1e5+5;
12 int n,a[NN],dis[NN],new_n;
13 int dp1[NN],dp2[NN];
14 struct SNOWtree{
15     #define lid (id<<1)
16     #define rid (id<<1|1)
17     #define mid ((l+r)>>1)
18     int maxn[NN<<2];
19     inline void insert(int id,int l,int r,int pos,int val){
20         if(l==r){maxn[id]=max(maxn[id],val);return;}
21         if(pos<=mid) insert(lid,l,mid,pos,val);
22         else insert(rid,mid+1,r,pos,val);
23         maxn[id]=max(maxn[lid],maxn[rid]);
24     }
25     inline int query(int id,int l,int r,int ql,int qr){
26         if(ql<=l && r<=qr) return maxn[id]; int ans=0;
27         if(ql<=mid) ans=max(ans,query(lid,l,mid,ql,qr));
28         if(qr>mid) ans=max(ans,query(rid,mid+1,r,ql,qr));
29         return ans;
30     }
31 }tr;
32 namespace WSN{
33     inline short main(){
34         freopen("b.in","r",stdin);
35         freopen("b.out","w",stdout);
36         n=read(); for(int i=1;i<=n;++i) dis[i]=a[i]=read();
37         sort(dis+1,dis+n+1); new_n=unique(dis+1,dis+n+1)-dis-1;
38         for(int i=1;i<=n;i++) a[i]=lower_bound(dis+1,dis+new_n+1,a[i])-dis+1;
39         double maxn=0.0;
40         for(int i=1;i<=n;i++){
41             int w1=tr.query(1,1,new_n,1,a[i]-1);
42             dp1[i]=w1+dis[a[i]-1];
43             maxn=max(maxn,dp1[i]*1.0);
44             tr.insert(1,1,new_n,a[i],dp1[i]);
45         }
46         memset(tr.maxn,0,sizeof(tr.maxn));
47         for(int i=n;i;i--){
48             int w2=tr.query(1,1,new_n,1,a[i]-1);
49             dp2[i]=w2+dis[a[i]-1];
50             tr.insert(1,1,new_n,a[i],dp2[i]);
51         }
52         // for(int i=1;i<=n;i++) cout<<dp1[i]<<" "<<dp2[i]<<endl;
53         for(int i=1;i<=n;i++){
54             maxn=max(maxn,(dp1[i]+dp2[i]-dis[a[i]-1])/2.0);
55         } printf("%.3lf\n",maxn);
56         return 0;
57     }
58 }
59 signed main(){return WSN::main();}

T3 矩阵

神仙大模拟

当$n>=3 ,m>=3$时，考虑一个图

+	-
-		+
	+	-

这样的一个小正方形按照上面的符号加起来如果不是$0$，那么他无解，

可以看出上面的是对每种操作都进行了一遍，行列斜都是一加一减

判断无解完成后考虑如何构造

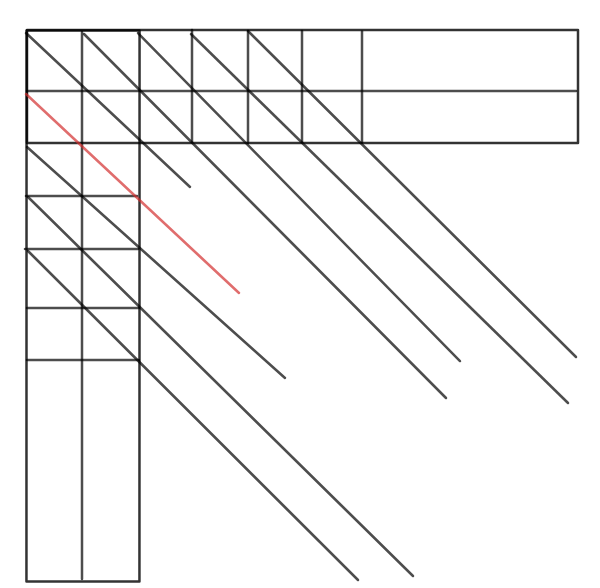
如图，每个斜线去消除，保证被削后的第二行和第一行相等，即$a[1][j+1]=a[2][j+1],j \in [1,m-1]$，这里只以列举例，

消行的让$a[i][1]=a[i][2],i \in[3,n]$，这样写是为了让红线特判，让他和$a[1][1]$相等，斜着干完列的竖着把列都干成$0$，

斜着干完行的把行干成$0$，这样就可以消完，因为不合法已经判掉，一定有解，注意要输出步数

 1 #include<bits/stdc++.h>
 2 #define int long long
 3 using namespace std;
 4 namespace AE86{
 5     inline int read(){
 6         int x=0,f=1;char ch=getchar();
 7         while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
 8         while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}return x*f;
 9     }inline void write(int x,char opt='\n'){
10         char ch[20];int len=0;if(x<0)x=~x+1,putchar('-');
11         do{ch[len++]=x%10+(1<<5)+(1<<4);x/=10;}while(x);
12         for(register int i=len-1;i>=0;--i)putchar(ch[i]);putchar(opt);}
13 }using namespace AE86;
14 const int NN=5005;
15 int n,m,a[NN][NN],step;
16 struct answer{
17     int opt,x,k;
18     inline void print(){write(opt,' ');write(x,' ');write(k,' ');puts("");}
19 }ans[NN];
20 // inline void print(){
21     // for(int i=1;i<=n;i++){
22     //     for(int j=1;j<=m;j++){
23     //         cout<<a[i][j]<<" ";
24     //     } cout<<endl;
25     // }
26 // }
27 inline void spj(){
28     cout<<m<<endl;
29     for(int j=1;j<=m;j++) printf("2 %lld %lld\n",j,-a[1][j]);
30 }
31 namespace WSN{
32     inline short main(){
33         freopen("c.in","r",stdin);
34         freopen("c.out","w",stdout);
35         n=read(); m=read();for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) a[i][j]=read();
36         if(n==1){spj(); return 0; }
37         if(n>=3 && m>=3) for(int i=1;i<=n-2;i++) for(int j=1;j<=m-2;j++)
38             if(a[i][j]-a[i][j+1]-a[i+1][j]+a[i+2][j+1]+a[i+1][j+2]-a[i+2][j+2]!=0) return puts("-1"),0;
39         for(int j=m-1;j;j--){
40             ans[++step]=(answer){3,j-1,a[1][j+1]-a[2][j+1]};
41             for(int jj=j,ii;jj<=m;jj++)
42                 ii=jj-ans[step].x, a[ii][jj]+=ans[step].k;
43         }
44         ans[++step]=(answer){3,1-2,a[1][1]-a[2][1]};
45         for(int jj=1,ii;jj<=m;jj++)
46             ii=jj-ans[step].x, a[ii][jj]+=ans[step].k;
47         for(int j=m;j;j--){
48             ans[++step]=(answer){2,j,-a[1][j]};
49             for(int i=1;i<=n;i++) a[i][j]+=ans[step].k;
50         }
51         // print(); return 0;
52         for(int i=3;i<=n;i++){
53             ans[++step]=(answer){3,1-i,a[i][2]-a[i][1]};
54             for(int ii=i,jj;ii<=n;ii++)
55                 jj=ii+ans[step].x, a[ii][jj]+=ans[step].k;
56         }
57         for(int i=3;i<=n;i++){
58             ans[++step]=(answer){1,i,-a[i][1]};
59             for(int j=1;j<=m;j++) a[i][j]+=ans[step].k;
60         }
61         write(step);
62         for(int i=1;i<=step;i++) ans[i].print();
63         return 0;
64     }
65 }
66 signed main(){return WSN::main();}

T4 花瓶

基础$dp$好想，但是时间都花在了$T1$上，没仔细打$T4$，然后就是斜率优化

比较妙的是排序，让复杂度少了一个二分凸包的$log$

 1 #include<bits/stdc++.h>
 2 #define int long long
 3 using namespace std;
 4 namespace AE86{
 5     inline int read(){
 6         int x=0,f=1;char ch=getchar();
 7         while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
 8         while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}return x*f;
 9     }inline void write(int x,char opt='\n'){
10         char ch[20];int len=0;if(x<0)x=~x+1,putchar('-');
11         do{ch[len++]=x%10+(1<<5)+(1<<4);x/=10;}while(x);
12         for(register int i=len-1;i>=0;--i)putchar(ch[i]);putchar(opt);}
13 }using namespace AE86;
14 const int NN=5005;
15 int n,s[NN],a[NN],id[NN];
16 int f[NN][NN],q[NN],l,r;
17 inline bool cmp(int a,int b){ return s[a]<s[b];}
18 namespace WSN{
19     inline short main(){
20         freopen("d.in","r",stdin);
21         freopen("d.out","w",stdout);
22         n=read(); for(int i=1;i<=n;i++) a[i]=read(),s[i]=s[i-1]+a[i],id[i]=i;
23         sort(id,id+n+1,cmp); memset(f,-0x3f,sizeof(f));
24         for(int i=0;i<=n;i++) f[i][0]=0;
25         for(int j=1;j<=n;j++){
26             l=1; r=0;
27             for(int k=0;k<=n;k++) if(id[k]<j){
28                 while(l<r && (f[j][q[r]]-f[j][q[r-1]])*(s[id[k]]-s[q[r-1]])<=(f[j][id[k]]-f[j][q[r-1]])*(s[q[r]]-s[q[r-1]])) --r;
29                 q[++r]=id[k];
30             }
31             for(int i=n;~i;i--) if(id[i]>j){
32                 while(l<r && (s[id[i]]-s[j])*(s[q[l+1]]-s[q[l]])<=(f[j][q[l+1]]-f[j][q[l]])) ++l;
33                 f[id[i]][j]=max(f[id[i]][j],f[j][q[l]]+(s[id[i]]-s[j])*(s[j]-s[q[l]]));
34             }
35         }
36         int maxn=0;    for(int i=0;i<n;i++) maxn=max(maxn,f[n][i]);
37         write(maxn);
38         return 0;
39     }
40 }
41 signed main(){return WSN::main();}