BUAA 2020 软件工程 个人项目作业

BUAA 2020 软件工程 个人项目作业

Author: 17373051 郭骏

项目	内容
这个作业属于哪个课程	2020春季计算机学院软件工程(罗杰 任健)
这个作业的要求在哪里	个人项目作业
我在这个课程的目标是	学习软件工程的开发知识，培养工程化开发能力
这个作业在哪个具体方面帮助我实现目标	通过实操掌握PSP开发基础

1.前言

• 教学班级：005
• 项目地址：https://github.com/sharinka0715/SE2020-Individual-Homework

给定 N 条直线，询问平面中有多少个点在至少 2 条给定的直线上。题目输入保证答案只有有限个。

2.PSP表格

PSP2.1	Personal Software Process Stages	预估耗时（分钟）	实际耗时（分钟）
Planning	计划	5	5
· Estimate	· 估计这个任务需要多少时间	5	5
Development	开发	250	490
· Analysis	· 需求分析 (包括学习新技术)	20	40
· Design Spec	· 生成设计文档	20	20
· Design Review	· 设计复审 (和同事审核设计文档)	5	5
· Coding Standard	· 代码规范 (为目前的开发制定合适的规范)	5	5
· Design	· 具体设计	60	60
· Coding	· 具体编码	60	60
· Code Review	· 代码复审	20	60
· Test	· 测试（自我测试，修改代码，提交修改）	60	240
Reporting	报告	70	70
· Test Report	· 测试报告	30	30
· Size Measurement	· 计算工作量	10	10
· Postmortem & Process Improvement Plan	· 事后总结, 并提出过程改进计划	30	30
	合计	325	565

3.解题思路（没写程序前）

暴力求解

对于这个题，最直接的求解方式是用暴力求解法。

• 1.对于每一条直线给出的两点，求出直线的一般式。
• 2.对这\(n\)条直线，每两条直线求一次交点，共需要求\(\frac{n(n-1)}{2}\)次交点。
• 3.对这\(\frac{n(n-1)}{2}\)个交点进行去重，暴力去重法需要每两个点比较一次。

这样做显然时间开销非常大，且时间复杂度最大的环节在第三步，会达到\(O(n^4)\)级别。

改进去重

对于判断两个点是否为同一个，我们可以通过改进数据结构的方式来进行。

我们使用哈希表来存储交点的坐标。每计算出一个坐标，就将它存入哈希表中。哈希表通过哈希函数直接计算寻址，通过判断寻址处有没有重复元素来判断是否重复。理想情况下，每次寻址均没有出现哈希冲突，则为\(m\)个点去重的时间复杂度为\(O(m)\)。

交点的个数对于平面上所有点来说是稀疏的，在哈希函数设计较好的情况下，可以很大程度上减少哈希冲突的发生，即使是最坏的情况下，也和暴力对比法开销相近。

改进求交点个数

在最坏情况下，我们确实需要对没两条直线都求一次交点。但是由简单的数学知识可知，当两条直线平行时，他们必然没有交点。所以，我们可以将互相平行的直线找出来并入同一组，在最后只需要对组间直线求交点即可。

假设\(n\)条直线中，有\(a_1\)条直线互相平行，又有\(a_2\)条直线互相平行……又有\(a_k\)条直线互相平行，且\(a_1+a_2+\cdots+a_k=n\)，每两组直线之间不平行，则这些直线的交点个数最多为\(\sum^{1\leq i,j\leq k}_{i\not=j}a_ia_j\)。显然，当所有的\(a_i\)并不全都为1的时候，交点个数是小于\(\frac{n(n-1)}{2}\)的。只要交点个数能够在去重之前变少，去重时的开销也必然变少。

下面我们来考虑如何判断直线平行。我们记录直线的斜率（平行于y轴特判），用斜率作为键建立哈希表，和上文同样的道理，为\(n\)条直线判断是否平行在理想情况下只需要\(O(n)\)的复杂度。

性能测试中，直线条数最多500000条，理论上最多可以产生1.25×10^11个交点，但交点个数限制在5000000以内，所以此类优化能够取得很大的效果，很难逼近最坏情况。

附加题：暴力求解

附加题依然采用暴力求解+哈希存储的方式解决。

• 对于直线和圆，将直线方程带入圆中可以解出坐标。可以提前判断直线和圆的距离来判断两者有无交点，如果有交点，再进行判别式的计算，可以节省一定的开销。
• 对于圆和圆，首先判断两圆的位置关系是否有相交，然后再将两者方程作差得到一条直线，这条直线过且只过他们的交点，可以将问题转化为圆和直线的问题，调用前面的函数即可解决。

4.设计实现过程

本次题目的工程量不算很大，也需要我们在一周内完成，所以我虽然使用的是C++语言，但不会特别强调到面向对象的特性。对于对象内的属性，也没有设置private去保护。这主要是为了增加程序性能。

代码整体上分为四个类：

• class Point：点类。存储点的坐标等相关信息。
• class Line：直线类。存储直线的斜率、纵轴截距。有计算和直线交点的方法。
• class Circle：圆类。附加题专用，存储圆的圆心坐标和半径。有计算和直线、圆交点的方法。
• class Individual：程序的主类。包含输入分析方法、数据存储方法、计算交点方法。核心在于unordered_set保存点的坐标。

关于垂直于y轴的直线：

定义极大常数INF特判，当斜率为INF时，截距值默认等于横轴截距。

因为所有输入均为整数，且数字有范围，所以斜率的最大值不可能超过200000。

这里设INF=500000。

单元测试的设计中，包含以下内容：

• 题目中所给的简单样例
• 边界条件，比如斜率不存在，以及交点的距离非常近
• 复杂情况，主要是多条直线交于多个点的手造数据。

在实现过程中，我发现，double类型的数据容易丢失精度，在去重的时候容易引起误判，且能够造出相关数据来导致误差。所以在实现的过程中，我控制前面所有的计算均使用long long类型来进行，在整个步骤中只进行一次除法，这样能够将double精度带来的的误差降至最低，经测验，能够通过我手造的特殊数据测试。

5.性能分析

以下是性能分析图。

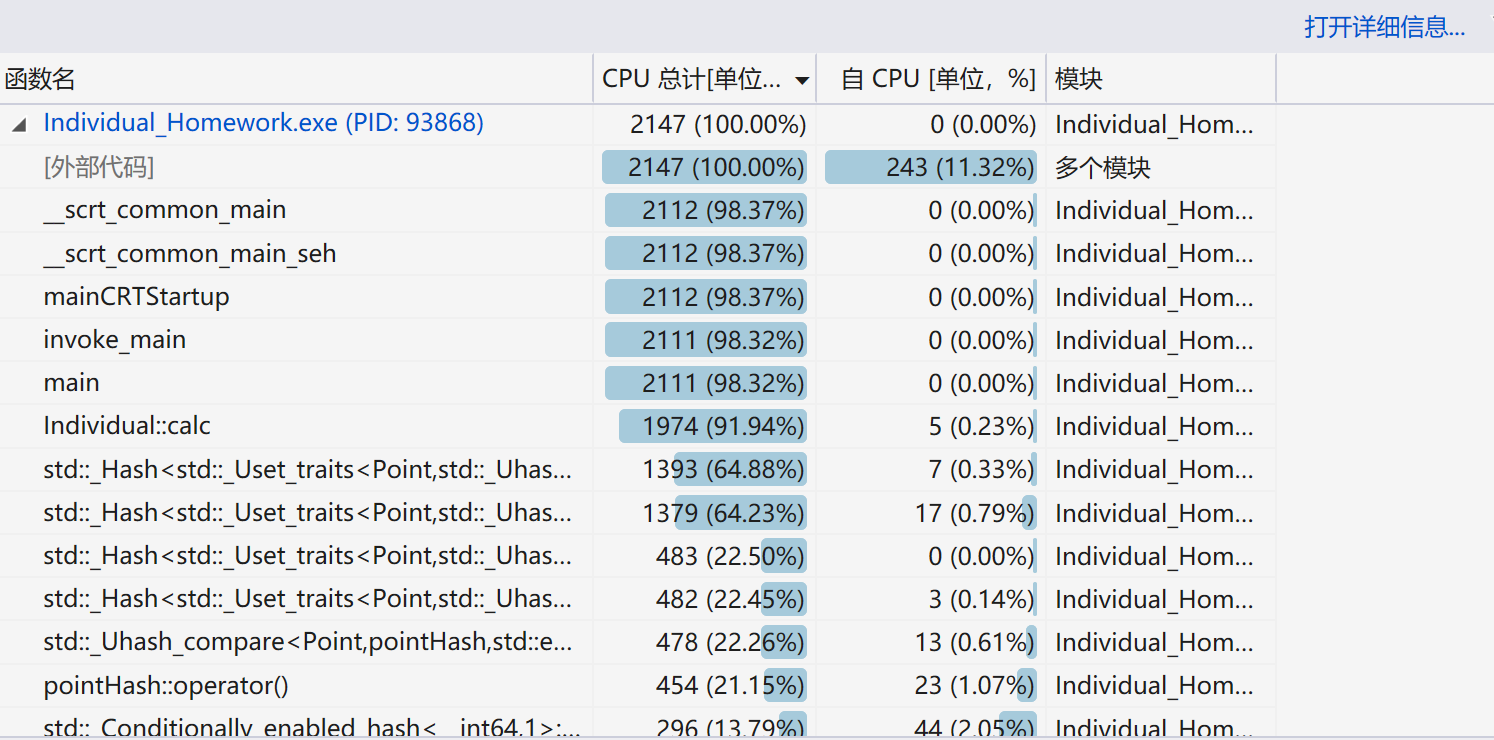
从图中可以看出，算法耗费时间最久的方法是calc方法，这个方法中，最耗时的函数又是insert函数。

显然，程序主要的时间都花在哈希函数的比较去重上。但是此块，我并没有想到非常好的优化方法，只能尽可能在其他地方寻找优化。

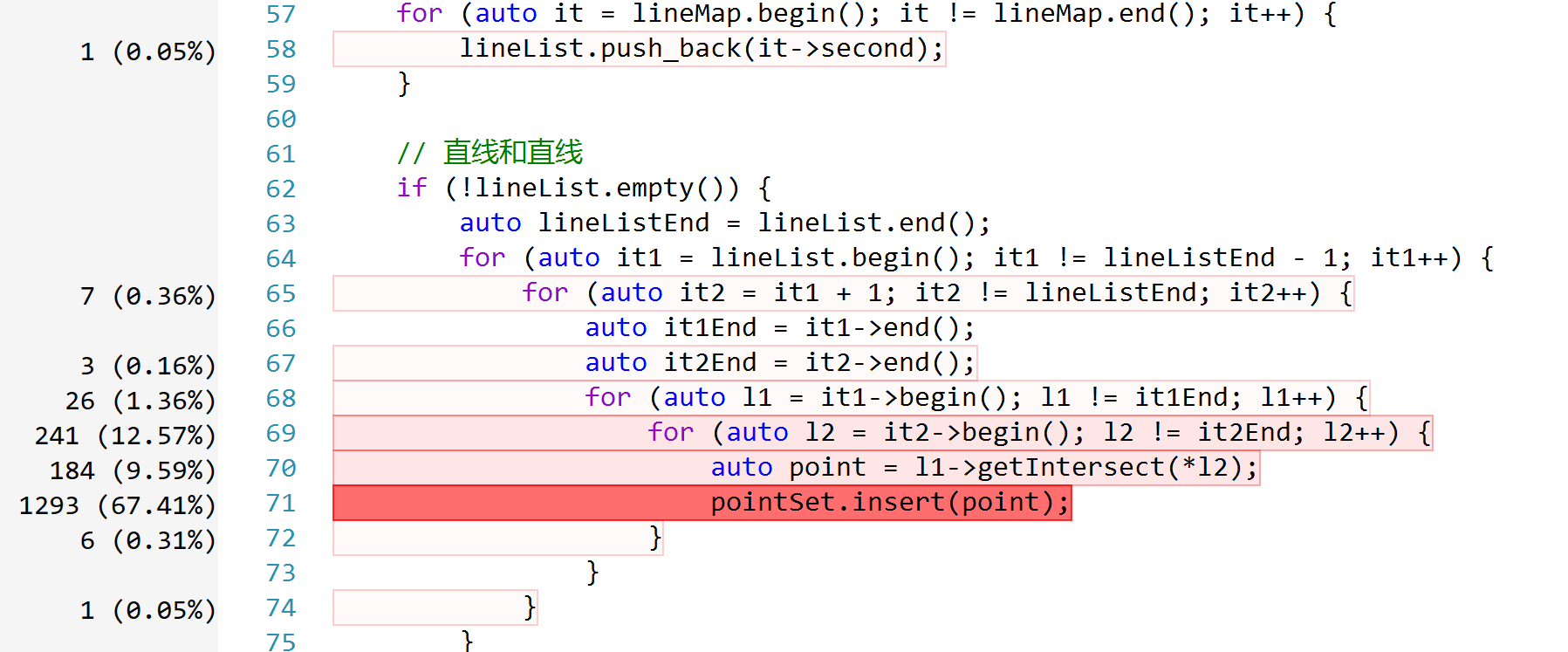
比如图中63、66、67行，将end()方法只调用一次，以静态存储的方式记录迭代器末尾的位置，而不是写在for循环的条件中，经验证，可以一定程度上降低CPU占用，所以我采用了这种写法。

6.代码说明

此处附上代码质量分析图、单元测试通过图、代码覆盖率图。

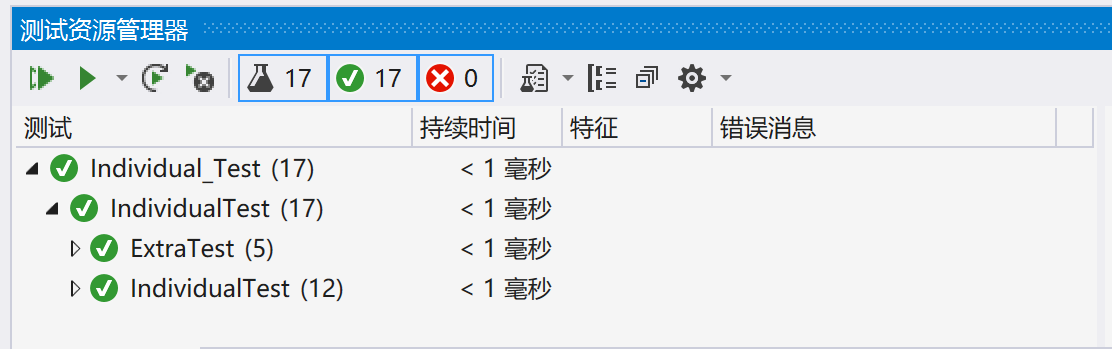
代码覆盖率并没有达到100%。原因是我在程序中写了一些冗余的函数。这些函数在执行过程中没有被调用，但是我并没有删掉他们，因为这些函数是最开始就写好的，以备不时之需而使用，如果需求有所增加，可以直接使用，但目前无法进行测试，也不会对当前程序运行带来影响。

另外没有覆盖到的内容还有对命令行参数的处理。我写了略微复杂的if逻辑结构，占用了main函数较大的篇幅，所以main.cpp看上去覆盖率较低。

关键代码如下所示。

// 求两条直线的交点
// 直线方程为kx-dy+b=0
Point Line::getIntersect(Line& geo) {
    // 没有实现两条直线平行时的特判
    // 判断直线斜率是否存在
    if (d == 0) {
        return Point(-b, k, -geo.k * b + geo.b, geo.d * k);
    }
    if (geo.d == 0) {
        return Point(-geo.b, geo.k, -k * geo.b + b, geo.k * d);
    }
    //这里计算出点坐标的分子(xu, yu)和分母(down)
    long long xu = geo.b * d - b * geo.d;
    long long yu = k * geo.b - geo.k * b;
    long long down = k * geo.d - geo.k * d;
    //在最后一步，建立点类时才做除法
    return Point(xu, down, yu, down);
}

// 求两个圆的交点
vector<Point> Circle::getIntersect(Circle& geo) {
    // 计算圆心间的距离，和半径作比较，确定两个圆有交点
    long long dl = (a - geo.a) * (a - geo.a) + (b - geo.b) * (b - geo.b);
    if (dl <= (r + geo.r) * (r + geo.r) && dl >= (r - geo.r) * (r - geo.r)) {
        // 计算出圆方程相减得到的直线方程
        long long xc = 2 * (geo.a - a);
        long long yc = -2 * (geo.b - b);
        long long c = a * a + b * b - r * r
            - geo.a * geo.a - geo.b * geo.b + geo.r * geo.r;
        Line tmp(xc, yc, c);
        // 创建临时直线，调用求交点方法
        return tmp.getIntersect(*this);
    }
    // 没有交点，返回空的向量
    return vector<Point>();
}