Noip模拟11 2021.7.11
T1 math
其实看看题面,看看给的那机组数据即可看出规律了(然而当时并没有,只是发现模数的循环节,存了个vector,接下来就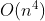 暴力了)
暴力了)
有个柿子: 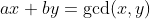 其实就是裴蜀定理。
其实就是裴蜀定理。
然后想一想的话就是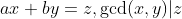
那么只要求出Ν个的gcd再和k求gcd,算出来之后用这个总的gcd去进行翻倍
反到最大的小于k的数停止即可


1 #include<bits/stdc++.h>
2 #define int long long
3 #define write(X) printf("%lld\n",X)
4 #define Min(A,B) ((A)<(B)?(A):(B))
5 using namespace std;
6 inline int read(){
7 int x=0,f=1; char ch=getchar();
8 while(ch<'0'||ch>'9'){ if(ch=='-') f=-1; ch=getchar(); }
9 while(ch>='0'&&ch<='9'){ x=(x<<1)+(x<<3)+(ch^48); ch=getchar(); }
10 return x*f;
11 }
12 const int NN=5e6;
13 int n,k,GCD,ans[NN],tot;
14 inline int gcd(int a,int b){
15 if(b==0) return a;
16 return gcd(b,a%b);
17 }
18 namespace WSN{
19 inline int main(){
20 n=read(),k=read();
21 GCD=gcd(read(),k);
22 for(int i=1;i<n;i++){ int a=read();GCD=gcd(GCD,a);}
23 // cout<<GCD<<endl;
24 for(int i=0;i<=k;i++){
25 if(GCD*i>=k) break;
26 ans[++tot]=GCD*i;
27 }
28 write(tot);
29 for(int i=1;i<=tot;i++) printf("%lld ",ans[i]);
30 return 0;
31 }
32 }
33 signed main(){return WSN::main();}
34 // FILE *A=freopen(".in","r",stdin);
35 // FILE *B=freopen("aaa.out","w",stdout);
T2 biology
这题当时一看是个dp就先去看T3了,T3水了个线段树回来干打了一个正确性颇高的贪心
正解的初始柿子还是很好想的,不过对于dp弱者来说循环就很麻烦。。。
可是,这题的循环也并不麻烦。。。
首先柿子:
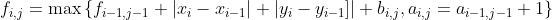
然后看上届大佬的题解里说道:
dp方程里面的绝对值要拆开!!!
然后可以得到四种不同的情况:
将绝对值拆开,四个二维树状数组分别维护最大值:
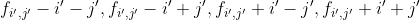
可以画图,将一个方块分成四块,田字格中点为(i,j),则从左上,左下,右上,右下的四个区域v向此处转移,按照绝对值划分可分为:

然后进行转移即可:


1 #include<bits/stdc++.h>
2 #define int long long
3 #define write(X) printf("%lld\n",X)
4 #define Max(A,B) ((A)>(B)?(A):(B))
5 using namespace std;
6 inline int read(){
7 int x=0,f=1; char ch=getchar();
8 while(ch<'0'||ch>'9'){ if(ch=='-') f=-1; ch=getchar(); }
9 while(ch>='0'&&ch<='9'){ x=(x<<1)+(x<<3)+(ch^48); ch=getchar(); }
10 return x*f;
11 }
12 const int NN=2005,MM=2005*2005,NM=1e6+5;
13 int n,m,a[NN][NN],b[NN][NN],cnt;
14 int f[NN][NN];
15 vector< pair< int,int > > vc[MM];
16 bool vis[MM];
17 struct SNOW{
18 int t[NN][NN];
19 inline int lobit(int x){return x&(-x);}
20 inline void update(int x,int y,int val){
21 for(int i=x;i<=n;i+=lobit(x)) for(int j=y;j<=m;j+=lobit(y)) t[i][j]=Max(t[i][j],val);
22 }
23 inline int query(int x,int y){
24 int ans=0;
25 for(int i=x;i;i-=lobit(x)) for(int j=y;j;j-=lobit(y)) ans=Max(ans,t[i][j]);
26 return ans;
27 }
28 }t1,t2,t3,t4;
29 int na[MM],rk[MM];
30 inline bool cmp(int a,int b){return a<b;}
31 namespace WSN{
32 inline int main(){
33 n=read(),m=read();
34 for(int i=1;i<=n;i++) for(int j=1;j<=m;j++){
35 a[i][j]=read();
36 if(!vis[a[i][j]] && a[i][j]) vis[a[i][j]]=1,na[++cnt]=a[i][j];
37 }
38 for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) b[i][j]=read();
39 sort(na+1,na+cnt+1,cmp);
40 for(int i=1;i<=cnt;i++) rk[na[i]]=i;
41 for(int i=1;i<=n;i++) for(int j=1;j<=m;j++)
42 if(a[i][j]) vc[rk[a[i][j]]].push_back(make_pair(i,j));
43 for(int i=0;i<vc[1].size();i++){
44 int x=vc[1][i].first,y=vc[1][i].second,vb=b[x][y];
45 t1.update(x,y,vb-x-y);t2.update(x,m-y+1,vb-x+y);t3.update(n-x+1,y,vb+x-y);t4.update(n-x+1,m-y+1,vb+x+y);
46 }
47 for(int i=2;i<=cnt;i++){
48 for(int j=0;j<vc[i].size();j++){
49 int x=vc[i][j].first,y=vc[i][j].second,vb=b[x][y];
50 f[x][y]+=Max(t1.query(x,y)+x+y+vb,Max(t2.query(x,m-y+1)+x-y+vb,Max(t3.query(n-x+1,y)-x+y+vb,t4.query(n-x+1,m-y+1)-x-y+vb)));
51 }
52 for(int j=0;j<vc[i].size();j++){
53 int x=vc[i][j].first,y=vc[i][j].second,v=f[x][y];
54 t1.update(x,y,v-x-y);t2.update(x,m-y+1,v-x+y);t3.update(n-x+1,y,v+x-y);t4.update(n-x+1,m-y+1,v+x+y);
55 }
56 }
57 int jie=0;
58 for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) jie=Max(jie,f[i][j]);
59 write(jie);
60 return 0;
61 }
62 }
63 signed main(){return WSN::main();}
然而这只是四十分的打法....
正解其实不用考虑各种合法状态,因为最优状态是唯一的,绝对值对于你转移的方向是有限制的(即对于其他不合法状态,也就是绝对值出现负数的情况一定没有出现正数优)。那么先将节点转移为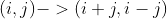 ,便可以只记录四个变量
,便可以只记录四个变量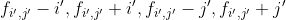 ,找出最大的一步合法状态即可。
,找出最大的一步合法状态即可。


1 #include<bits/stdc++.h>
2 #define int long long
3 #define write(X) printf("%lld\n",X)
4 #define Max(A,B) ((A)>(B)?(A):(B))
5 using namespace std;
6 inline int read(){
7 int x=0,f=1; char ch=getchar();
8 while(ch<'0'||ch>'9'){ if(ch=='-') f=-1; ch=getchar(); }
9 while(ch>='0'&&ch<='9'){ x=(x<<1)+(x<<3)+(ch^48); ch=getchar(); }
10 return x*f;
11 }
12 const int NN=2005,MM=2005*2005,NM=1e6+5;
13 int n,m,a[NN][NN],b[NN][NN],cnt;
14 int f[NN][NN];
15 vector< pair< int,int > > vc[MM];
16 bool vis[MM];
17 int t1,t2,t3,t4;
18 int na[MM],rk[MM];
19 inline bool cmp(int a,int b){return a<b;}
20 namespace WSN{
21 inline int main(){
22 n=read(),m=read();
23 for(int i=1;i<=n;i++) for(int j=1;j<=m;j++){
24 a[i][j]=read();
25 if(!vis[a[i][j]] && a[i][j])
26 vis[a[i][j]]=1,na[++cnt]=a[i][j];
27 }
28 for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) b[i][j]=read();
29 sort(na+1,na+cnt+1,cmp);
30 for(int i=1;i<=cnt;i++) rk[na[i]]=i;
31 for(int i=1;i<=n;i++)
32 for(int j=1;j<=m;j++)
33 if(a[i][j]) vc[rk[a[i][j]]].push_back(make_pair(i+j,i-j));
34 for(int i=0;i<vc[1].size();i++){
35 int x=vc[1][i].first,y=vc[1][i].second,opx=x+y>>1,opy=x-y>>1,vb=b[opx][opy];
36 t1=Max(t1,vb-x); t2=Max(t2,vb+x); t3=Max(t3,vb-y); t4=Max(t4,vb+y);
37 }
38 for(int i=2;i<=cnt;i++){
39 for(int j=0;j<vc[i].size();j++){
40 int x=vc[i][j].first,y=vc[i][j].second,opx=x+y>>1,opy=x-y>>1,vb=b[opx][opy];
41 int ans1=t1+vb+opx+opy,ans2=t2+vb-opx-opy,ans3=t3+vb+opx-opy,ans4=t4+vb-opx+opy;
42 int ans=Max(ans1,Max(ans2,Max(ans3,ans4)));
43 f[opx][opy]+=ans;
44 }
45 for(int j=0;j<vc[i].size();j++){
46 int x=vc[i][j].first,y=vc[i][j].second,opx=x+y>>1,opy=x-y>>1,v=f[opx][opy];
47 t1=Max(t1,v-x); t2=Max(t2,v+x); t3=Max(t3,v-y); t4=Max(t4,v+y);
48 }
49 }
50 int jie=0;
51 for(int i=1;i<=n;i++) for(int j=1;j<=m;j++)
52 jie=Max(jie,f[i][j]);
53 write(jie);
54 return 0;
55 }
56 }
57 signed main(){return WSN::main();}
T3 english
这个题首先一看小的点线段树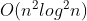 可过,不过大的点就很吓人。。。。
可过,不过大的点就很吓人。。。。
所以,对于预处理,应该处理出 表示序列第i个数之前(包括他)的第j位一共有多少个1
表示序列第i个数之前(包括他)的第j位一共有多少个1
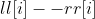 表示a[i]是区间内最大值的左端点和右端点。
表示a[i]是区间内最大值的左端点和右端点。
那么对于opt==1的情况,运用单调栈扫一边即可。还要注意疑惑对a[k]的贡献,有一个柿子:
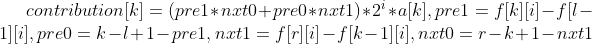
k,l,r分别表示循环到的序列第k位,以其为最大值的左/右端点。i表示二进制位数。
然后就是opt==2。。。。
这是个可持久化trie树,还没学,于是花了一下午和一晚上学习了主席树和可持久化trie。。。太男了
trie树在查找的时候也是维护了一个类似前缀和的东西。


1 #include<bits/stdc++.h>
2 #define int long long
3 #define write(X) printf("%lld\n",X)
4 #define Min(A,B) ((A)<(B)?(A):(B))
5 #define Max(A,B) ((A)>(B)?(A):(B))
6 using namespace std;
7 inline int read(){
8 int x=0,f=1; char ch=getchar();
9 while(ch<'0'||ch>'9'){ if(ch=='-') f=-1; ch=getchar(); }
10 while(ch>='0'&&ch<='9'){ x=(x<<1)+(x<<3)+(ch^48); ch=getchar(); }
11 return x*f;
12 }
13 const int mod=1e9+7,NN=1e5+5;
14 int n,opt,w[NN],ans1,ans2,ll[NN],rr[NN];
15 int pw[35],f[NN][35];
16 stack<int> s,t;
17 struct tree{
18 int ch[NN*22][2],siz[NN*22],root[NN*22],node;
19 void insert(int pre,int &now,int i,int x){//前驱点 当前点 最大递归位数 插入值
20 now=++node;
21 siz[now]=siz[pre];
22 if(i<0){siz[now]++;return;}
23 int bo=(x>>i)&1;
24 ch[now][bo^1]=ch[pre][bo^1];
25 insert(ch[pre][bo],ch[now][bo],i-1,x);
26 siz[now]=siz[ch[now][0]]+siz[ch[now][1]];
27 }
28 void insert(int x,int pos){insert(root[pos-1],root[pos],20,x);}
29 int query(int x,int y,int p){//在x~y区间内的1的个数
30 int pos=root[p],ans=0;
31 for(int i=20;i>=0;i--){
32 int a=(x>>i)&1,b=(y>>i)&1;
33 if(!b){
34 ans+=siz[ch[pos][a^1]];
35 pos=ch[pos][a];
36 }else pos=ch[pos][a^1];
37 if(!pos) break;
38 }
39 return ans;
40 }
41 }trie;
42 void work(int k,int l,int r){
43 for(int i=0;i<=20;i++){
44 int pre1=f[k][i]-f[l-1][i],pre0=k-l+1-pre1,nxt1=f[r][i]-f[k-1][i],nxt0=r-k+1-nxt1;
45 ans1=(ans1+pw[i]*(pre1*nxt0%mod+pre0*nxt1%mod)%mod*w[k]%mod)%mod;
46 }
47 }
48 void search(int k,int l,int r){
49 if(k-l<r-k){
50 for(int i=l;i<=k;i++)
51 ans2=(ans2+(trie.query(w[i],w[k],r)-trie.query(w[i],w[k],k-1))*w[k]%mod)%mod;
52 }
53 else{
54 for(int i=k;i<=r;i++)
55 ans2=(ans2+(trie.query(w[i],w[k],k)-trie.query(w[i],w[k],l-1))*w[k]%mod)%mod;
56 }
57 }
58 namespace WSN{
59 inline int main(){
60 n=read(),opt=read();
61 for(int i=1;i<=n;i++) {w[i]=read();trie.insert(w[i],i);}
62 pw[0]=1;
63 for(int i=1;i<=20;i++) pw[i]=2*pw[i-1];
64 for(int i=1;i<=n;i++){
65 while(!s.empty()&& w[i]>w[s.top()]) s.pop();
66 if(s.empty()) ll[i]=1;
67 else ll[i]=s.top()+1;
68 s.push(i);
69 }
70 for(int i=n;i>=1;i--){
71 while(!t.empty()&& w[i]>=w[t.top()]) t.pop();
72 if(t.empty()) rr[i]=n;
73 else rr[i]=t.top()-1;
74 t.push(i);
75 }
76 for(int i=1;i<=n;i++) for(int j=0;j<=20;j++)
77 {f[i][j]+=f[i-1][j]; if((w[i]>>j)&1) f[i][j]++;}
78 for(int i=1;i<=n;i++) work(i,ll[i],rr[i]);
79 for(int i=1;i<=n;i++) search(i,ll[i],rr[i]);
80 if(opt==1) write(ans1);
81 else if(opt==2) write(ans2);
82 else {write(ans1); write(ans2);}
83 return 0;
84 }
85 }
86 signed main(){return WSN::main();}
87 // FILE *A=freopen("english3.in","r",stdin);
88 // FILE *B=freopen("aaa.out","w",stdout);
End
此次考试较为上次聪明了一点,总归是并没有执着于正解而不去打暴力,可是对于正解的思考还是较少,下次考试应该注意打暴力的速度和正确性以及留给正解的思考时间
Noip模拟11 2021.7.11的更多相关文章
- Noip模拟74 2021.10.11
T1 自然数 考场上当我发现我的做法可能要打线段树的时候,以为自己百分之百是考虑麻烦了 但还是打了,还过掉了所有的样例,于是十分自信的就交了 正解还真是线段树,真就第一题数据结构 但是包括自己造的小样 ...
- Noip模拟36 2021.8.11
刚题的习惯还是改不了,怎么办??? T1 Dove打扑克 考场上打的动态开点线段树+并查集,考后发现自己像一个傻子,并查集就行.. 这几天恶补数据结构疯了 用树状数组维护后缀和,$siz_i$表示编号 ...
- Noip模拟7 2021.6.11
前言 考试时候der展了,T1kmp没特判(看来以后还是能hash就hash),T2搜索细节没注意,ans没清零,130飞到14.... T1 匹配(hash/kmp) 这太水了,其实用个hash随便 ...
- Noip模拟50 2021.9.10
已经好长时间没有考试不挂分的良好体验了... T1 第零题 开场数据结构,真爽 对于这道题首先要理解对于一条链从上向下和从下向上走复活次数相等 (这可能需要晚上躺在被窝里面脑摸几种情况的样例) 然后就 ...
- NOIP模拟赛(洛谷11月月赛)
T1 终于结束的起点 题解:枚举啊... 斐波那契数 第46个爆int,第92个爆long long.... 发现结果一般是m的几倍左右....不用担心T. #include<iostream ...
- Noip模拟70 2021.10.6
T1 暴雨 放在第一道的神仙题,不同的做法,吊人有的都在用线段树维护$set$预处理 我是直接$dp$的,可能代码的复杂度比那种的稍微小一点 设$f[i][j][p][0/1]$表示考虑了前$i$列, ...
- Noip模拟76 2021.10.14
T1 洛希极限 上来一道大数据结构或者单调队列优化$dp$ 真就没分析出来正解复杂度 正解复杂度$O(q+nm)$,但是据说我的复杂度是假的 考虑一个点转移最优情况是从它上面的一个反$L$形转移过来 ...
- Noip模拟69 2021.10.5
考场拼命$yy$高精度结果没学好$for$循环痛失$50pts$,当场枯死 以后一定打对拍,要不考后会... T1 石子游戏 首先要知道典型的$NIM$博弈,就是说如果所有堆石子个数的异或和为$0$则 ...
- Noip模拟63 2021.9.27(考场惊现无限之环)
T1 电压机制 把题目转化为找那些边只被奇数环包含. 这样的话直接$dfs$生成一棵树,给每个点附上一个深度,根据其他的非树边都是返祖边 可以算出环内边的数量$dep[x]-dep[y]+1$,然后判 ...
随机推荐
- C# 动态构建表达式树(二)——构建 Select 和 GroupBy 的表达式
C# 动态构建表达式树(二)--构建 Select 和 GroupBy 的表达式 前言 在上篇中写了表达式的基本使用,为 Where 方法动态构建了表达式.在这篇中会写如何为 Select 和 Gro ...
- JavaScript进行表单提交
表单结构,设置form表单的id属性,method="post/get","action"要跳转的页面(jsp或servlet) <form name=& ...
- 开源的物联网技术平台(Thingsboard)
1 总体说明 1.1 产品概述 1.1.1 Thingsboard作用 1.置备并控制设备. 2.采集设备数据并进行数据可视化. 3.分析设备数据,触发告警. 4.将数据传输到另一个系统. 5 ...
- Java基础系列(14)- JavaDoc生成文档
JavaDoc JavaDoc是一种将注释生成HTML文档的技术,生成的HTML文档类似于Java的API,易读且清晰明了 参数信息 @author 作者名 @version 版本号 @since 指 ...
- Linux系列(25) - 常用快捷键(未更新完)
快捷键 说明 Ctrl+L 清屏 tab tab按一次自动补全目录文件名称/tab按二次将目录下带有补全前面字段的所有文件目录展示出来,例子: cd / tab键按两次将根目录下所有文件展示出来 ...
- Shell系列(9)- 用户自定义变量(2)
定义变量 变量名=变量值 例如: x=123 mulu="当前目录下有 $(ls)" 备注: 变量名只能是字母.下划线.数字组成且不能以数字开头 变量等号两侧不能加空格 若变量值中 ...
- sonar扫描java项目报错
安装maven 配置path 验证maven,看到以下信息证明已经成功 扫描项目 扫描以下项目: kf-buss-nhgip-smartoffice-business-thirdparty 项目的配置 ...
- jmeter之聚合报告(Aggregate Report)
jmeter最常用的listener--聚合报告Aggregate Report,每一个字段的具体含义是什么? Label:每个请求的名称.每个 JMeter 的 element(例如 HTTP Re ...
- python学习笔记(十二)-网络编程
本文结束使用 Requests 发送网络请求.requests是一个很实用的Python HTTP客户端库,编写爬虫和测试服务器响应数据时经常会用到.可以说,Requests 完全满足如今网络的需求. ...
- 彻底关闭Windows自动更新
win+r--输入services.msc(服务管理窗口)停止windows update服务并禁用同时在恢复里,改为无操作 win + r --输入gpedit.msc(本地组策略编辑器)家庭版没有 ...
