P4779 【模板】单源最短路径（标准版）单源最短路Dijkstra

题目描述

给定一个$n$个点，$m$条有向边的带非负权图，请你计算从$s$出发，到每个点的距离。

数据保证你能从$s$出发到任意点。

输入格式

第一行为三个正整数$n,m,s$。 第二行起$m$行，每行三个非负整数 $u_i, v_i, w_i​$，表示从$u_i​$到$v_i$有一条权值为$w_i$的有向边。

输出格式

输出一行$n$个空格分隔的非负整数，表示$s$到每个点的距离。

输入输出样例

输入

4 6 1
1 2 2
2 3 2
2 4 1
1 3 5
3 4 3
1 4 4

输出

0 2 4 3

样例解释

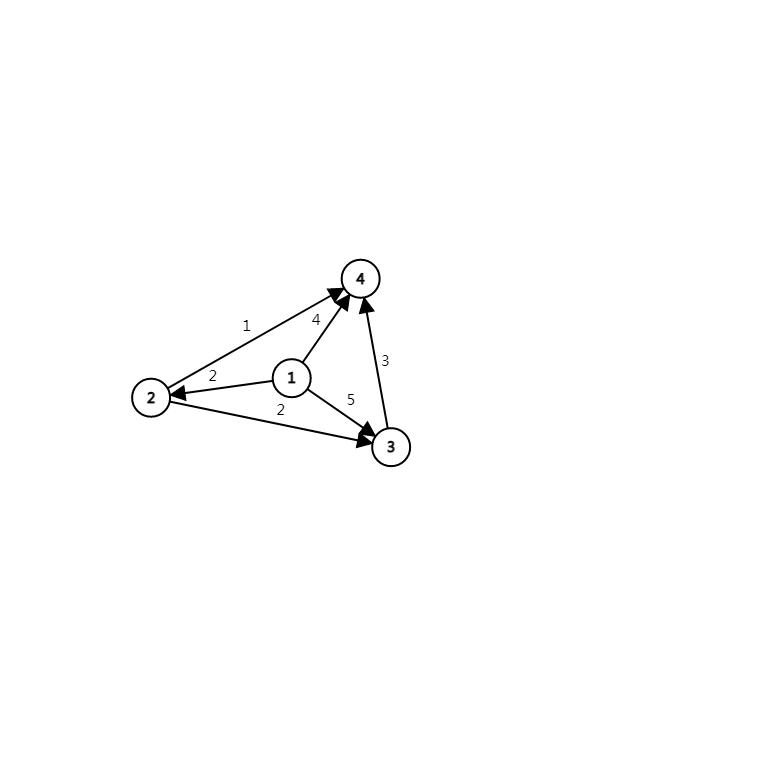
由$1\rightarrow 1$，距离为$0$，由$1\rightarrow 2$，距离为$2$，由$1\rightarrow 3$，距离最小等于$1\rightarrow 2\rightarrow 3 = 4$，由$1\rightarrow 4$，距离最小等于$1\rightarrow 2\rightarrow 4 = 3$

分析

模板题，裸$Dijkstra$即可

代码

#include <bits/stdc++.h>

#define Enter puts("")
#define Space putchar(' ')

using namespace std;

typedef long long ll;
typedef double Db;

inline ll Read()
{
    ll Ans = 0;
    char Ch = getchar() , Las = ' ';
    while(!isdigit(Ch))
    {
        Las = Ch;
        Ch = getchar();
    }
    while(isdigit(Ch))
    {
        Ans = (Ans << 3) + (Ans << 1) + Ch - '0';
        Ch = getchar();
    }
    if(Las == '-')
        Ans = -Ans;
    return Ans;
}

inline void Write(ll x)
{
    if(x < 0)
    {
        x = -x;
        putchar('-');
    }
    if(x >= 10)
        Write(x / 10);
    putchar(x % 10 + '0');
}

const int MAXN = 100010 , MAXM = 500010;

struct Edge
{
    int To , Dis , Next;
};

Edge E[MAXM];
int Head[MAXN] , Dis[MAXN] , Count;
bool Visit[MAXN];
int n , m , s;

inline void Add_Edge(int u , int v , int d)
{
    E[++Count].Dis = d;
    E[Count].To = v;
    E[Count].Next = Head[u];
    Head[u] = Count;
}

struct Node
{
    int Dis;
    int Position;
    bool operator < (const Node &x)const
    {
        return x.Dis < Dis;
    }
};

priority_queue <Node> Q;

inline void Dijkstra()
{
    Dis[s] = 0;
    Q.push((Node) {0 , s});
    while(!Q.empty())
    {
        Node Temp = Q.top();
        Q.pop();
        int x = Temp.Position , d = Temp.Dis;
        if(Visit[x])
            continue;
        Visit[x] = 1;
        for(int i = Head[x]; i; i = E[i].Next)
        {
            int y = E[i].To;
            if(Dis[y] > Dis[x] + E[i].Dis)
            {
                Dis[y] = Dis[x] + E[i].Dis;
                if(!Visit[y])
                    Q.push((Node) {Dis[y] , y});
            }
        }
    }
}

int main()
{
    n = Read();
    m = Read();
    s = Read();
    for(int i = 1; i <= n; i++)
        Dis[i] = 0x7fffffff;
    for(int i = 0; i < m; i++)
    {
        int u , v , d;
        u = Read();
        v = Read();
        d = Read();
        Add_Edge(u , v , d);
    }
    Dijkstra();
    for(int i = 1; i <= n; i++)
        Write(Dis[i]) , Space;
    return 0;
}