遥远的国度 （树链剖分换根），洛谷P3979

析：显然，若没有换根操作，则为树链剖分板子题，但是这道题我们考虑换根操作

　　考虑这样一个性质：在一棵树上，两点的距离路径是唯一的！！

　　也就是说，我们在修改路径上的点权时，不必考虑根在哪里，直接利用模板修改即可

　　麻烦的地方在于查询操作，我分了三种情况来讨论：（设 root 为当前的根，id 为当前要查询的编号）

　　1.若 deep[id]>=deep[root]　，则跟对他没有影响，直接查询即可

　　2.若 deep[id]<deep[root] ,刚开始我是求出两点的 LCA ，然后查询 (1,num[lca]) 和 （num[root]+size[root],n）

　　但是，这样会出现一些问题，比如这张图：

　　

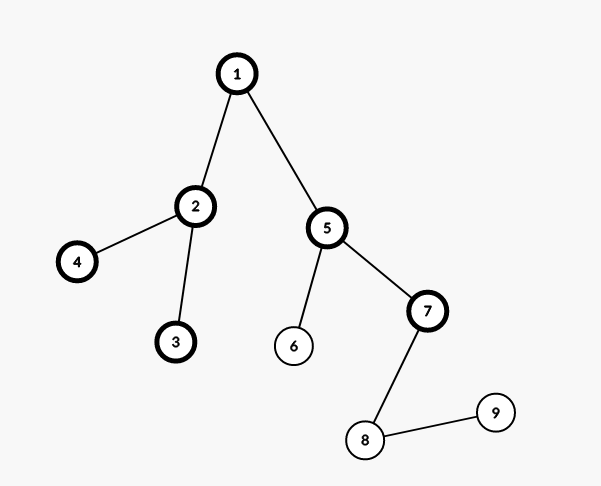
　　当 root=7,id==5 时，我们这样查询就会漏掉 6

　　那么我们能不能这样写呢 ？ 查询(1,num[root]-1) 和（num[root]+size[root],n）;

　　显然也是不能的（虽然这数据比较水，这样写会多得几分），如下图：

　　

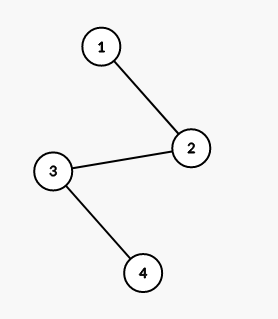
　　当 root==4 ,id==2 时，这样查询就会多出来一个点 3

　　这...........可如何是好？

　　其实，应该有大佬已经发现了，无论是什么情况，我们查询的边界始终是 （1，num[son[lca]]-1）和 （num[son[lca]+size[son[lca]]] , n）

　　所以，我们只需查询 root 和 id 的 lca 的重儿子即可（保证在同一条链上）

代码如下：

#include<bits/stdc++.h>
#define re register int
#define next nett
#define lc rt<<1
#define rc rt<<1|1
#define mid ((l+r)>>1)
#define ii inline int
#define iv inline void
using namespace std;
const int N=1e6+10;
struct CUN
{
	int minn,lazy;
}use[N<<4];
int n,m,root,timi,tot,lcas;
int to[N<<1],next[N<<1],head[N],num[N],top[N],son[N],deep[N],fa[N],size[N],chu[N],zh[N];
inline int read()
{
	int x=0,f=1;
	char ch=getchar();
	while(ch<'0'||ch>'9')
	{
		if(ch=='-')
			f=0;
		ch=getchar();
	}
	while(ch>='0'&&ch<='9')
	{
		x=(x<<1)+(x<<3)+(ch^48);
		ch=getchar();
	}
	return (f)?x:(-x);
}
ii add(int x,int y)
{
	to[++tot]=y;
	next[tot]=head[x];
	head[x]=tot;
}
iv dfs1(int st,int f)
{
	size[st]=1;
	fa[st]=f;
	deep[st]=deep[f]+1;
	for(re i=head[st];i;i=next[i])
	{
		int p=to[i];
		if(p==f)
			continue;
		dfs1(p,st);
		size[st]+=size[p];
		son[st]=(size[son[st]]>size[p])?son[st]:p;
	}
}
iv dfs2(int st,int t)
{
	top[st]=t;
	num[st]=++timi;
	zh[timi]=chu[st];
	if(!son[st])
		return;
	dfs2(son[st],t);
	for(re i=head[st];i;i=next[i])
	{
		int p=to[i];
		if(p==fa[st]||p==son[st])
			continue;
		dfs2(p,p);
	}
}
iv pp(int rt)
{
	use[rt].minn=min(use[lc].minn,use[rc].minn);
}
iv build(int rt,int l,int r)
{
	if(l==r)
	{
		use[rt].minn=zh[l];
		return;
	}
	build(lc,l,mid);
	build(rc,mid+1,r);
	pp(rt);
}
ii gett(int x,int y)
{
	int fx=top[x],fy=top[y];
	while(fx!=fy)
	{
		if(deep[fx]<deep[y])
			swap(x,y),swap(fx,fy);
		if(fa[fx]==y)
			return fx;
		x=fa[fx];
		fx=top[x];
	}
	if(deep[x]>deep[y])
		swap(x,y);
	return son[x];
}
iv pd(int rt,int l,int r)
{
	if(use[rt].lazy)
	{
		use[lc].minn=use[rt].lazy;
		use[rc].minn=use[rt].lazy;
		use[lc].lazy=use[rc].lazy=use[rt].lazy;
		use[rt].lazy=0;
	}
}
iv change(int rt,int l,int r,int L,int R,int z)
{
	if(R<l||r<L||L>R) return ;
	if(L<=l&&r<=R)
	{
		use[rt].minn=z;
		use[rt].lazy=z;
		return;
	}
	pd(rt,l,r);
	if(mid>=L)
		change(lc,l,mid,L,R,z);
	if(mid<R)
		change(rc,mid+1,r,L,R,z);
	pp(rt);
}
ii query(int rt,int l,int r,int L,int R)
{
	if(R<l||r<L||L>R) return 999999999;
	if(L<=l&&r<=R)
		return use[rt].minn;
	pd(rt,l,r);
	if(mid>=R)
		return query(lc,l,mid,L,R);
	if(mid<L)
		return query(rc,mid+1,r,L,R);
	return min(query(lc,l,mid,L,R),query(rc,mid+1,r,L,R));
}
iv upd(int x,int y,int z)
{
	int fx=top[x],fy=top[y];
	while(fx!=fy)
	{
		if(deep[fx]<deep[fy])
			swap(x,y),swap(fx,fy);
		change(1,1,n,num[fx],num[x],z);
		x=fa[fx];
		fx=top[x];
	}
	if(deep[x]>deep[y])
		swap(x,y);
	change(1,1,n,num[x],num[y],z);
}
int main()
{
	n=read();
	m=read();
	int a,b,c,d,lca;
	for(re i=1;i<n;i++)
	{
		a=read();
		b=read();
		add(a,b);
		add(b,a);
	}
	for(re i=1;i<=n;i++)
		chu[i]=read();
	root=1;
	dfs1(root,root);
	dfs2(root,root);
	build(1,1,n);
	root=read();
	while(m--)
	{
		a=read();
		if(a==1)
		{
			root=read();
			continue;
		}
		if(a==2)
		{
			b=read();
			c=read();
			d=read();
			upd(b,c,d);
		}
		if(a==3)
		{
			b=read();
			if(b==root)
			{
				printf("%d\n",query(1,1,n,1,n));
				continue;
			}
			lcas=gett(b,root);
			if(deep[b]>=deep[root])
				printf("%d\n",query(1,1,n,num[b],num[b]+size[b]-1));
			else if(fa[lcas]==b)
				printf("%d\n",min(query(1,1,n,1,num[lcas]-1),query(1,1,n,num[lcas]+size[lcas],n)));
			else
				printf("%d\n",query(1,1,n,num[b],num[b]+size[b]-1));
			continue;
		}

	}
	return 0;
}