C#深度复制和浅度复制

C#深度复制和浅度复制

复制一个值变量很简单，新建一个变量然后将原来的变量赋值过去就行，但是复制一个引用变量这种方法是不行的，如果不明白为什么可以先看看这篇解释

引用类型变量和值类型变量在赋值时的不同

如果要复制一个引用类型的变量，比如说类，需要在类定义中继承ICloneable接口，并实现Clone方法，这是一个固定格式，下面看一个例子

 public class Test:ICloneable
 {
     public int Val;
     public object Clone() => MemberwiseClone();
 }

定义了一个Test类，继承ICloneable接口，实现Clone方法，实现Clone方法的格式是固定的，这里使用了简化写法，public object Clone() => MemberwiseClone();等于

public object Clone()
{
    return MemberwiseClone();
}

这是C#提供的方法，按照这么写就对了，此时如果要复制一个Test类的引用变量，就可以这么写

Test t1 = new Test();
Test t2 = (Test)t1.Clone();

有一个引用类型变量t1，调用t1.Clone()会在堆中重新开辟一个内存空间，并且复制t1堆空间的值，然后会返回这个新空间的内存地址，因为Clone()方法返回类型是object，所以强制类型转换为Test，然后赋给Test类型的变量t2

这个过程，便是C#中的浅度复制(ShallowCopy)，也有称为影子复制的

这个复制会存在一些问题，那就是一个引用类型中存在引用类型字段时，引用类型字段并不会也复制一份

public class Test:ICloneable
{
    public int Val;
    public Test2 Z = new Test2();
    public object Clone()
    {
        return MemberwiseClone();
    }
}
public class Test2
{
    public int D;
}

这里定义了两个类，其中Test类中包含了一个Test2类型的引用类型变量Z，我们先看内存中怎样表示的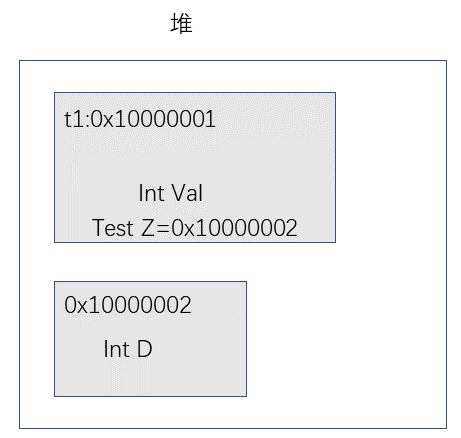

从这张图我们可以看到，当我们使用Clone对引用类型进行Clone时，只会复制堆空间的值，如果堆空间中有引用类型，在复制时就只单纯的复制了引用类型的堆空间地址，这样的后果就是虽然Clone得到了两个堆空间对象，但是堆空间对象中的字段却指向了同一个另外的空间地址，在某些情况下就会出现问题

所以

浅度复制：解决了直接使用赋值运算符时变量指向了同一个堆空间的问题（即Test t2 = t1的问题），但是只解决了一层，对于包含在内的堆空间中的成员的引用没有进一步解决（即t1.Z和t2.Z指向了同一个堆空间地址）

为了解决上述问题，就需要使用深度复制，深度复制的基本思路，就是在Clone方法中创建一个新的对象并使其内容与现有内容保持一致（其实是废话），我们甚至可以不用继承ICloneable，但是建议继承并使用Clone方法，这样可以保持方法名的一致性

至于怎么实现，可以自行思考（主要是我也在思考中）

所以这篇文章的主要内容是讲：C#提供的return MemberwiseClone();只是浅度复制，不会为引用成员创建新空间并将引用成员空间的值复制过去，只会复制引用成员的空间地址，需要注意