P1908 逆序对——树状数组&离散化&快读快写の学习

题目简述：

对于给定的一段正整数序列，逆序对就是序列中 a_i>a_jai​>aj​ 且 i<ji<j 的有序对。

输出序列中逆序对的数目。

知识补充：

树状数组：

这东西就是就是用数组来模拟树形结构，在解决区间上的更新以及求和问题时速度为O(logn₎，速度比普通数组要快很多)

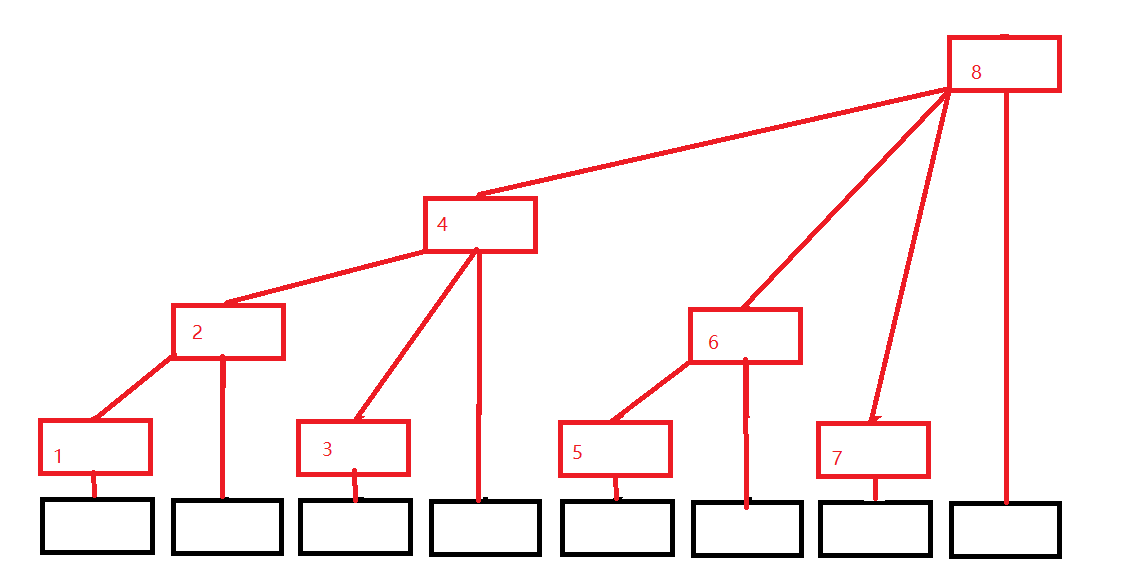
很重要的一点，那就是：在写代码的时候，把树状数组当成一个普通数组来思考，千万不要将树状数组计算的过程带入思考过程，不然搅死你。

1.单点修改&区间查询

单点增加（初始化）：题目：https://www.luogu.com.cn/problem/P3374

void add(int a,int b)
{
    for(;a<=n;a+=a&-a) c[a]+=b;
}

区间查询：

int ask(int a)
{
    int sum=0;
    for(;a;a-=a&-a) sum+=c[a];
    return sum;
}

上代码：

#include<bits/stdc++.h>
using namespace std;
int n,m;
int c[500005];
int d,e,f;
void add(int a,int b)
{
    for(;a<=n;a+=a&-a) c[a]+=b;
}

int ask(int a)
{
    int sum=0;
    for(;a;a-=a&-a) sum+=c[a];
    return sum;
}

int main()
{
    cin>>n>>m;
    for(int i=1;i<=n;i++)
    {
        int k;
        cin>>k;
        add(i,k);
    }
    for(int i=1;i<=m;i++)
    {
        cin>>d>>e>>f;
        if(d==1) add(e,f);
        if(d==2) cout<<tot(f)-tot(e-1)<<endl;
    }
    return 0;
}

2.区间修改&单点查询

这里要用到差分的思想，总体思想是将单点查询转化为差分的区间查询，区间的增加转化为差分的变化。

与上一种不同的是，这里需要一个普通数组来计算差。

上代码：题目：https://www.luogu.com.cn/problem/P3368

#include<bits/stdc++.h>
using namespace std;
int n,m;
long long del[500005];//差分的树状数组
long long ch[500005];//初始数组，其实只有在输入算差的时候才有一点用处
int o,x,y,k;
void add(int a,int b)//区间增加
{
    for(;a<=n;a+=a&-a) del[a]+=b;
    return  ;
}
void  chafen(int a,int b,int c)//差分的思想，先将【a,n】的所有差+c,再将【b+1,n】的所有差-c
{
    add(a,c);
    add(b+1,-c);
}
int sum(int a)//单点查询
{
    int ans=0;
    for(;a;a-=a&-a) ans+=del[a];
    return ans;
}
int main()
{
    cin>>n>>m;
    for(int i=1;i<=n;i++)
    {
        cin>>ch[i];
        add(i,ch[i]-ch[i-1]);//初始化
    }
    for(int i=1;i<=m;i++)
    {
        cin>>o;
        if(o==1)
        {
            cin>>x>>y>>k;
            chafen(x,y,k);
        }
        if(o==2)
        {
        cin>>k;
        cout<<sum(k)<<endl;
        }
    }
    return 0;
}

3.区间修改&区间查询（还没学呢~）

看了一下午，总算会了（bushi

主要还是我太菜了，看不懂网上大佬们专业的数学表示方法。

来推导一下过程：

（D[i]:用于存储前i项差分的树状数组。）

A[1]=D[1]

A[2]=D[1]+D[2]

A[3]=D[1]+D[2]+D[3]

。。。。。。。。。。。

A[i]=D[1]+D[2]+...+D[i]

相加，可以得到：

A[1]+A[2]+A[3]+...A[i]=D[1]*i+D[2]*(i-1)+...D[i]*1;

=n(D[1]+D[2]+D[3]+...D[i])-(D[1]*0+D[2]*1+D[3]*2+...D[i]*(i-1))

不难发现，除了D[i],我们还需要记录D[i]*(i-1)，就能求出前缀和了。

值得注意的是，在add和ask操作中，一开始要先记录下n的大小，因为n的大小在每一次操作中是固定的。

上代码：

#include<bits/stdc++.h>
using namespace std;
const int N=1e5+5;
int sum[N];
int sum1[N] ;
int n1;
int l,r;
int k;
int a[N];
void add(int n,int k){
    int i=n;//记录 n值
    for(;n<=n1;n+=n&-n){
        sum[n]+=k;
        sum1[n]+=k*(i-1);
    }
}
int ask(int n){
    int ans=0;
    int i=n;//记录n值
    for(;n>0;n-=n&-n){
        ans+=sum[n]*i-sum1[n];
    }
    return ans;
}
int main(){
    cin>>n1;
    for(int i=1;i<=n1;i++){
        cin>>a[i];
        add(i,a[i]-a[i-1]);
    }
    add(l,k);
    add(r,-k);//区间修改
    cin>>l>>r;
    cout<<ask(r)-ask(l-1); //区间查询
}

下一步就是学线段树了，冲冲冲！

离散化

这种东西有什么用呢？举个例子吧：

10 100 1000用桶储存起来，问比1000小的有多少个。

1 2 3的结果会与上面那组数据相同，但他只找两次，而上边要找989次。

相当于减少了一些无用功。

直接看代码吧（记住就行）：

#include<iostream>
#include<cstdio>
#include<algorithm>
using namespace std;
int lsh[1000], lshcopy[1000], sy[1000]; //lsh[n]是即将被离散化的数组，lshcopy[n]是a[n]的副本，sy[n]用于排序去重后提供离散化后的值
int main()
{
    int n;
    scanf("%d",&n);
    for(int i=0;i<n;i++)
    {
        scanf("%d",&sy[i]);
        lshcopy[i]=sy[i];

    }
    sort(sy,sy+n);//第一步排序
    for(int i=0;i<n;i++)
    {
        cout<<'('<<sy[i]<<')';
        cout<<"\n";
    }
    int size=unique(sy,sy+n)-sy;//unique显示去重后的个数
    printf("size is : %d",size);
    printf("\n");
    for(int i=0;i<n;i++)
    {
        lsh[i]=lower_bound(sy,sy+size,lshcopy[i])-sy; //即lsh[i]为lshcopy[i]离散化后对应的值
        printf("lsh is : %d",lsh[i]);
    }
}
 

快读快写：

快读：

int read(){
    int w=0;bool f=0;
    char ch=getchar();
    while(!isdigit(ch)){if(ch=='-')f=1;ch=getchar();}
    while(isdigit(ch)){w=(w<<3)+(w<<1)+ch-'0';ch=getchar();}
    w=f?-w:w;
    return w;
}

快写：

void write(long long x){
    if(x<0){
        putchar('-');
        x=-x;
    }
    if(x>9)write(x/10);
    putchar(x%10+'0');
    return;
}

题目分析：传送门：https://www.luogu.com.cn/problem/P1908

维护一个树状数组，用于维护当前各个数字的出现次数。

for example:

6
5 4 2 6 3 1
注意！要从后向前！
1 2 3 4 5 6
          1 ————此时1前面，没有任何的数，ans=0;
1 2 3 4 5 6
    1     1 ————这里3，6已经·可以组成一个逆序对了，利用区间查询ask函数可以算出来。
后同理。
记得离散化就行。
代码：

#include<bits/stdc++.h>
using namespace std;
const int N=5e5+10;
long long tree[N];
int s[N];
int scopy[N];
int ls[N];
int n;
long long ans=0;
int read(){
    int w=0;bool f=0;
    char ch=getchar();
    while(!isdigit(ch)){if(ch=='-')f=1;ch=getchar();}
    while(isdigit(ch)){w=(w<<3)+(w<<1)+ch-'0';ch=getchar();}
    w=f?-w:w;
    return w;
}
void write(long long x){
    if(x<0){
        putchar('-');
        x=-x;
    }
    if(x>9)write(x/10);
    putchar(x%10+'0');
    return;
}
void add(int a,int b)
{
    for(;a<=N-10;a+=a&-a) tree[a]+=b;
}

long long ask(int a)
{
    long long tot=0;
    for(;a;a-=a&-a)tot+=tree[a];
    return tot;
}

int main()
{
    n=read();
    for(int i=1;i<=n;i++)
    {
        s[i]=read();
        scopy[i]=s[i];
    } 

    sort(s+1,s+n+1);
    int size=unique(s+1,s+n+1)-s;
    for (int i=1;i<=n;i++)
    {
        ls[i]=lower_bound(s+1,s+size+1,scopy[i])-s;
    }

    for(int i=n;i>=1;i--)
    {
        add(ls[i],1);
        ans+=ask(ls[i]-1);
    }
    write(ans);
    return 0;
}

完结撒花~