感知机vs支持向量机

感知机
原理：二维空间中找到一条直线可以把所有二元类别分离开，三维或多维空间中，找到一个分离超平面把所有二元类别分离开。而可把所有二元类别分离开的超平面不止一个，哪个是最好的呢？
损失函数：所有误分类的点到超平面的总距离，找到损失函数最优化对应的超平面，即误分类的点到超平面总距离最小的模型参数w,b(感知机模型)
超平面定义
          wTx+b=0 w超平面法向量，b超平面截距
感知机和SVM的区别：

感知机目标找到一个超平面将各样本尽可能分离正确（有无数个）；SVM目标找到一个超平面不仅将各样本尽可能分离正确，还要使各样本离超平面距离最远（只有一个），SVM的泛化能力更强

SVM(Support Vector Machine)

1.线性可分支持向量机（Hard-Margin SVM-硬间隔最大化模型)：要求所有点都正确划分的基础上，找到间隔最大的分离超平面
2.线性支持向量机（Soft-Margin SVM-软间隔最大化模型）：相对与硬间隔模型放宽了限制，引入了松弛变量，使得分类器具有一定的容错性，容许有一些误分类的点
3.线性不可分支持向量机（核函数）：对于线性不可分问题将样本从原始空间通过核函数映射到高维空间实行“线性可分”

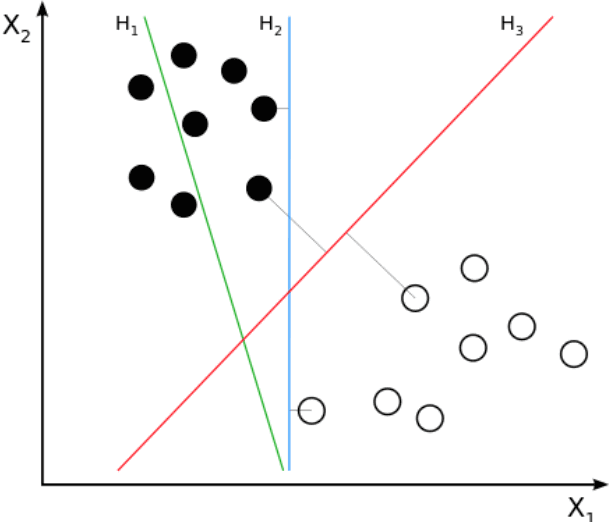
感知机的目标就是找到一个分割平面，使得尽量得区分正确（如下图）

SVM的目标是找到一个分割平面，不仅区分正确，而且要让正负样本尽量远离这个分割平面

下图里面，H2就是感知机的（不一定唯一），H3就是SVM的。