KKT原理以及SVM数学的理论推导分析

一直很好奇机器学习实战中的SVM优化部分的数学运算式是如何得出的，如何转化成了含有内积的运算式，今天上了一节课有了让我很深的启发，也明白了数学表达式推导的全过程。

对于一个SVM问题，优化的关键在于

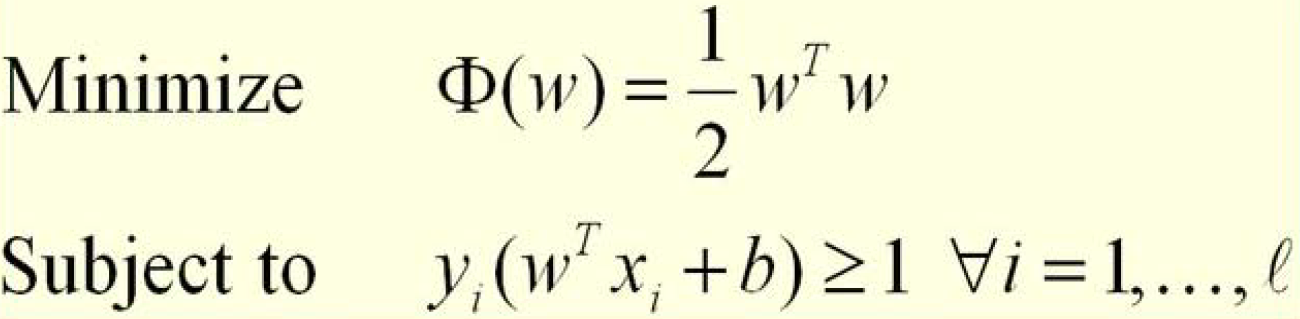
KKT理论所标明的是在拉格朗日乘数法中引入的系数与上面的不等式约束条件的乘积等于0始终成立，这个条件所保证的是优化问题的解存在，对于上面的优化，从线性空间的角度来思考就是在做最大化最小间隔，是一个非常明显的二次优化问题。本身分析到这里，还不足以说明问题，为何会出现含有内积的运算式呢。

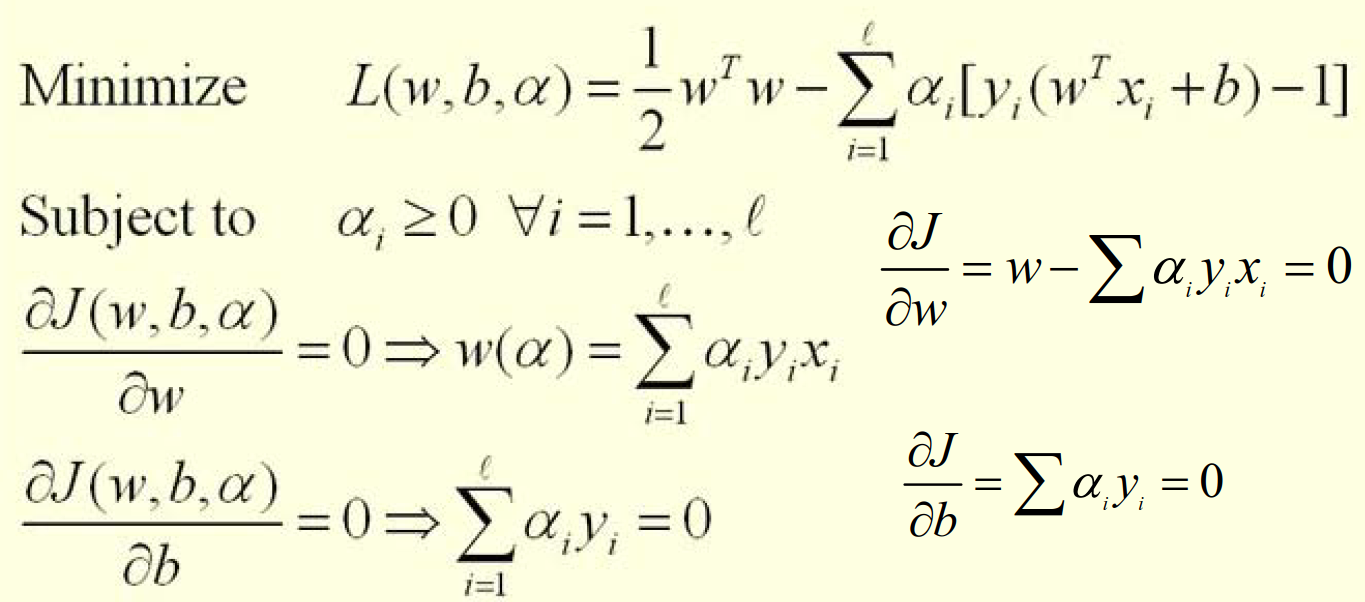
从这个拉格朗日求解函数的运算式出发，我们发现再优化问题的一般解中会始终有L对所有变量的偏导数均为0，这是多元函数取得极值的必要条件；

在这里，对wT的求导仍然与w是一致的，我们发现w其实是关于α的函数；其实本身每一个拉格朗日乘数都会对分类有影响，对于多数的αi，值都是0，而少数不为0的αi则是真正的支持向量，用于确定分类界限。

在获得w与α的关系后，将式子带回用于求解wT*w，可以得到

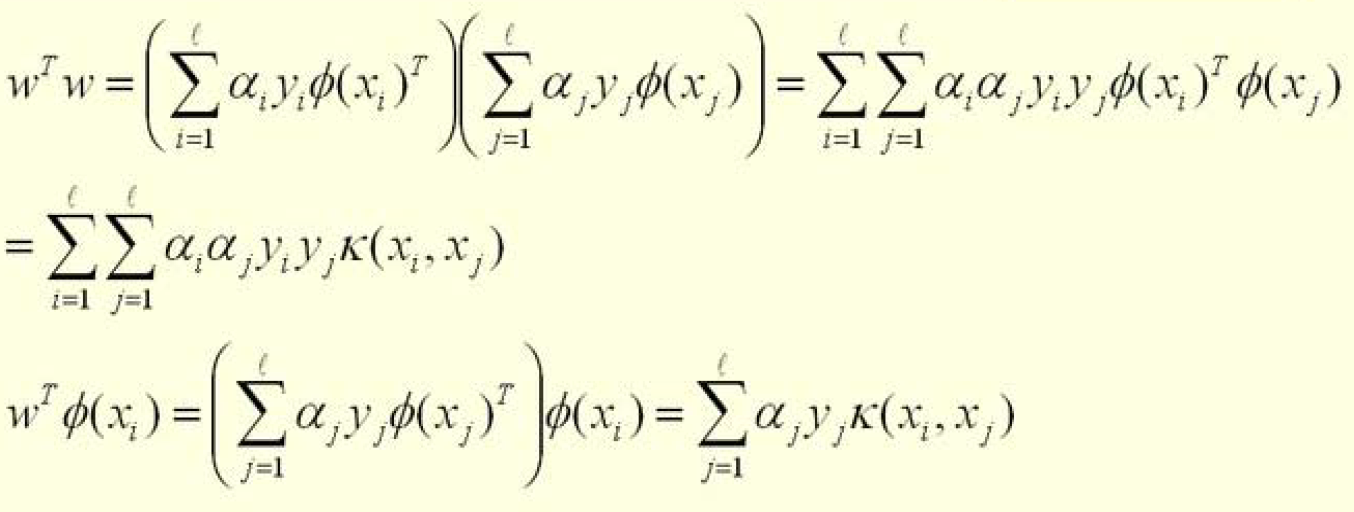
可以看到如果没有进行kernel变换那么将会以<xi,xj>的内积形式出现，进行kernel变换后则修正为kernel矩阵进行处理。

对原函数进行修正可以得到上面的结论，也就真正的写成了机器学习实战中的数学表达形式，这里y相当于书中的label；

启发：

对于整个过程而言并没有真正的对二次优化问题进行求解，而只是在形式上不断地进行等价变化，真正的求解要用到二次优化求解的相关理论，比如Platt的SMO算法，进行α对修正完成优化过程。这里的Σ表达形式与矩阵的乘积表达形式可以转化，这个在实际用程序解决问题时非常重要，利用矩阵形式处理数据是一个非常重要的思想观点，笔者以为矩阵才是数据的基本形式，实数域只是在线性空间上做了退化。同时，kernel与非kernel之间的形式也并没有过多差别，本质上的区分在于是在原空间进行内积运算还是对样本进行升维后进行内积运算，而kernel变换中的Φ映射我们本身并不关心，但升维后的内积运算可以通过kernel矩阵完成，这才是kernel变换最核心的东西。