K-Means聚类算法的原理及实现【转】

【转】http://www.aboutyun.com/thread-18178-1-1.html

问题导读：
1、如何理解K-Means算法？
2、如何寻找K值及初始质心？
3、如何应用K-Means算法处理数据？

K-Means是聚类算法中的一种，其中K表示类别数，Means表示均值。顾名思义K-Means是一种通过均值对数据点进行聚类的算法。K-Means算法通过预先设定的K值及每个类别的初始质心对相似的数据点进行划分。并通过划分后的均值迭代优化获得最优的聚类结果。

K值及初始质心

K值是聚类结果中类别的数量。简单的说就是我们希望将数据划分的类别数。K值决定了初始质心的数量。K值为几，就要有几个质心。选择最优K值没有固定的公式或方法，需要人工来指定，建议根据实际的业务需求，或通过层次聚类(Hierarchical Clustering)的方法获得数据的类别数量作为选择K值的参考。这里需要注意的是选择较大的K值可以降低数据的误差，但会增加过拟合的风险。

以下是一组用户的年龄数据，我们将K值定义为2对用户进行聚类。并随机选择16和22作为两个类别的初始质心。

<ignore_js_op>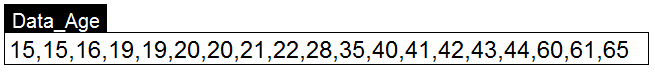 
<ignore_js_op>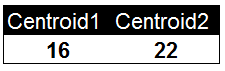

计算距离并划分数据

我们以图的形式展示聚类的过程。在这组年龄数据中，我们选择了16和22作为两个类别的初始质心，并通过计算所有用户的年龄值与初始质心的距离对用户进行第一次分类。
<ignore_js_op>

计算距离的方法是使用欧式距离。以下是欧式距离的计算公式。距离值越小表示两个用户间年龄的相似度越高。

<ignore_js_op>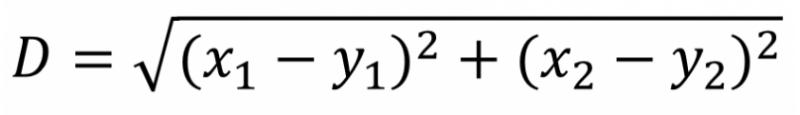

通过计算，我们获得了每个年龄数据点与两个初始质心的距离。这里我们以黑色实心圆点标记较大的距离值，空心圆点标记较小的距离值。例如第一个数据点15，到第一个初始质心16的距离为1，到第二个初始质心22的距离为7。相比之下15与16的距离更近，距离值为1，并以空心圆点标记。因此15这个年龄数据点被划分在第一个组(16)中。如果年龄数据点到两个初始质心的距离相等，可以划分到任意组中，例如年龄数据点19，到16和22的距离都为3。在这个示例中我们将数据点19划分到第二个组(22)中。
<ignore_js_op>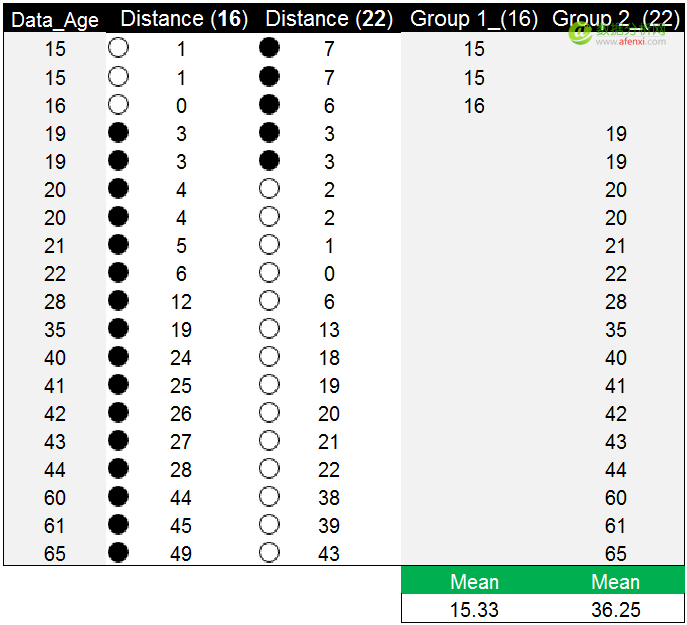

按相似程度（距离）对数据分完组后，分别计算两个分组中数据的均值15.33和36.25，并以这两个均值作为新的质心。在下图中可以看到，蓝色的数字为初始质心，红色的数字为新的质心。目前的质心和新的质心并不是同一个数据点，我们将以新的质心替代初始质心，迭代计算每个数据点到新质心的距离。直到新的质心和原质心相等，算法结束。
<ignore_js_op>

使用均值作为新质心

将两个分组中数据的均值作为新的质心，并重复之前的方法计算每个年龄数据点到新质心的距离。下面是年龄数据点到两个新质心的距离。以年龄数据点19为例，到新质心15.33的距离为3.67，到另一个新质心36.25的距离为17.25。相比之下数据点19到15.33的距离更近，为3.67。因此被分到第一组(15.33)中。
<ignore_js_op>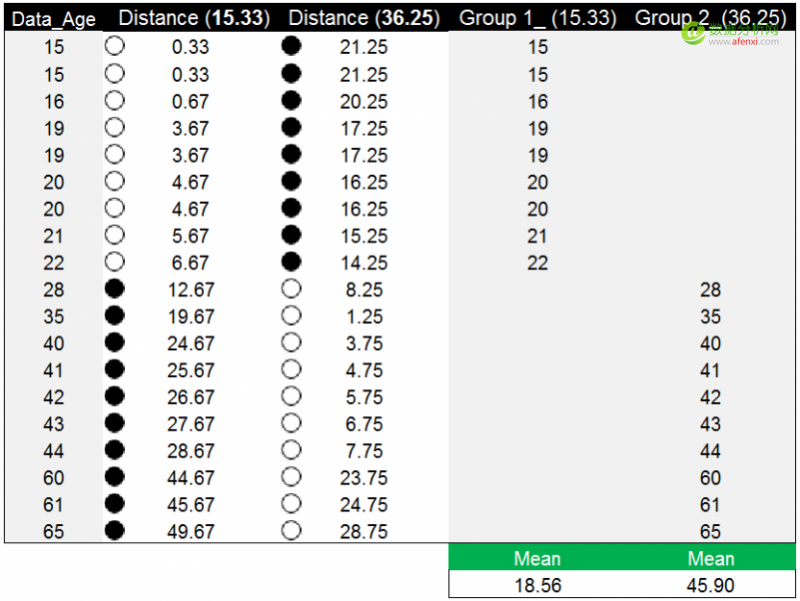

以年龄数据点到新质心的距离值完成分组后，再次计算两组的均值18.56和45.90，并以均值作为新质心替代原质心。下图中蓝色数字为原质心，红色数字为新质心。在新质心下，年龄数据的分组情况发生了变化，但新质心与原质心没有重合。

<ignore_js_op>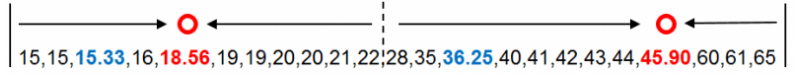

重复之前的方法和步骤，计算年龄数据点到新质心的距离。并对比数据点到两个新质心的距离，选择较小的距离值对年龄数据点进行分组。年龄数据点28到18.56的距离为9.44，到45.90的距离为17.90。因此年龄数据点28被分配到第一个18.56的分组中。
<ignore_js_op>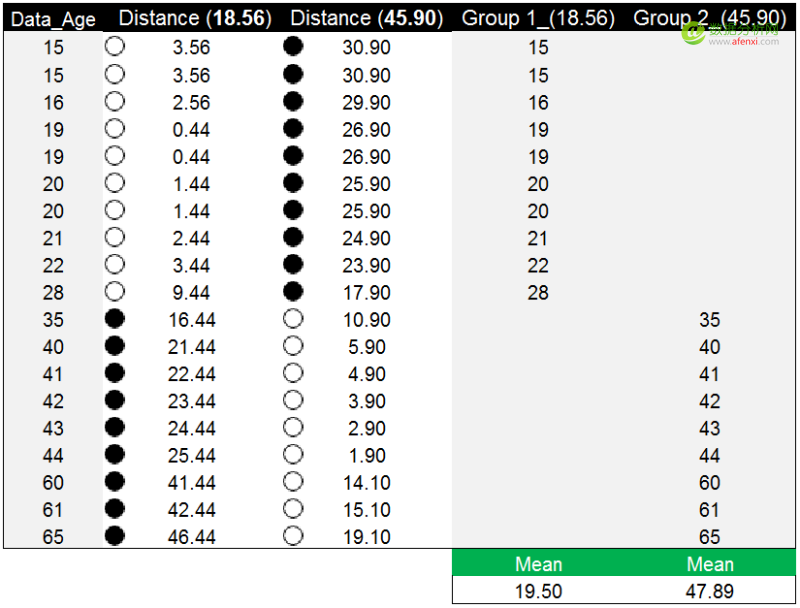

再次以年龄数据点到新质心的距离完成分组后，新质心（红色）与原质心（蓝色）仍然没有重合，但与之前相比分组的调整已经很小。我们继续计算新分组的均值19.50和47.89，并将均值作为新质心替代原质心。
<ignore_js_op>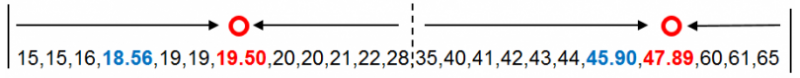

算法停止条件

开始计算的第一步我们说迭代计算每个数据到新质心的距离，直到新的质心和原质心相等，算法结束。使用上一步分组的均值19.50和47.89作为新质心。并计算年龄数据点到新质心的距离。以下为计算结果。
<ignore_js_op>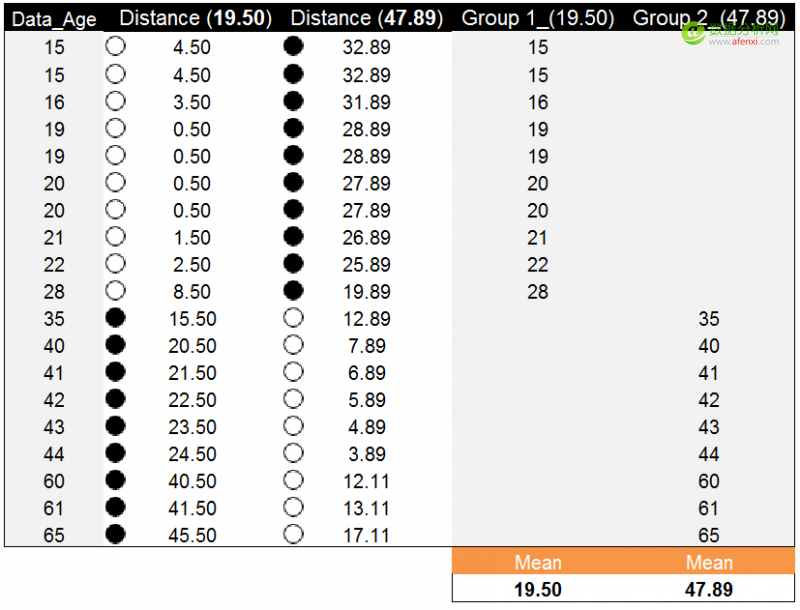

按照年龄数据点到新质心的距离对数据进行分组，并计算每组的均值作为新质心。这里两组的均值与原质心相等。也就是说新质心与原质心相等，都是19.50和47.89.。算法停止计算。年龄数据点被划分为两类，如下图所示分别为15-28和35-65。
<ignore_js_op>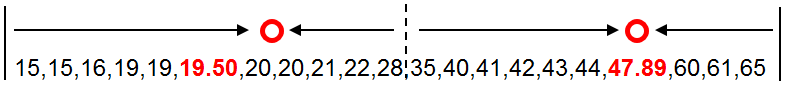

来源：蓝鲸碎碎念