四元数－－结合《real time rendering》中关于四元数部分

　　四元数产生于1843年，是复数的一个扩展，所以里面包含了一些复数的运算。直到1985年才在图形学中使用。

　　四元数的优势是，相对与矩阵和欧拉角，四元数更直观和方便。四元数还可以用作某些方向上的插值，而欧拉角可能并不能很好的完成。

　　四元数使用四个数字表示。通常，前三个和旋转的轴密切相关，最后一个和旋转的角度相关。以下是一些数学背景，对于后面的四元数的变化十分重要。

注意到四元数是复数的一个扩展，那么可以表示为：Û = (â, v), 其中 v 是一个实数，而 â 则是可以看成是虚部，且 â＝ i*q_x + j*q_y + k*q_z  其中，i j k 都是虚部，他们的计算为

i² = j²= k² = -1 ， jk = -kj=i , ik = -ki = j , ij = -ji = k ,因为â 含有三个部分，所以，一些向量的操作也是可以用在四元数的虚部上。

对于两个四元数相乘，如下图：

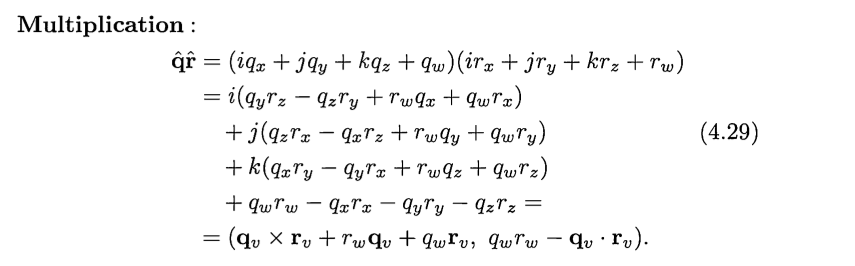
　　关于其他计算如下：

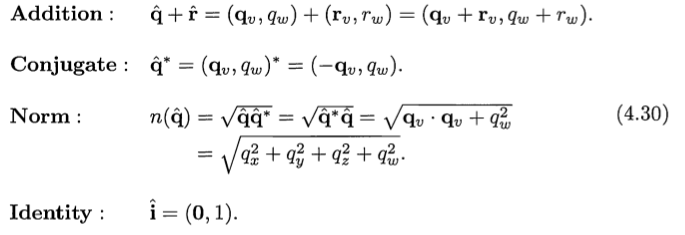
其中 conjugate 是共轭的意思。根据norm运算我们可以推出除法运算：

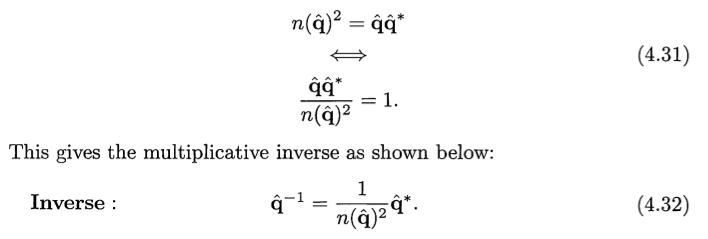
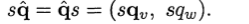
　　以及其他一些运算规则：

　　　对于单位四元数，我们还可以用下面的方法进表示，这也是表达旋转变化比较直观的方式

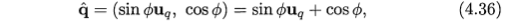
　　   其计算过程如下，其中要求u_q是单位向量：

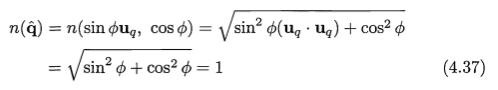
　　  另一种表达方式如下，其可以解决log和平方运算：

对于单位四元数的直观理解如下图：

　　以上是四元数的基本知识背景。下面来介绍四元数表示的变化。

我们只使用四元数中的一个子集，单位四元数来进行各种旋转变化，十分简单和强大。变化方程为：

　　其q是一个单位四元数，其形式为公式4.36，而p则是一个四次其次的点或者向量，p的每个部分直接代替四元数的各个部分，形成一个新的四元数。注意到q是单位四元数，所以q^－1 ＝ q^＊。而且，单位四元数与实数相乘并不能改变四元数的作用效果，所以四元数q 和－q的作用效果一样的。那么在从矩阵转化到四元数的过程中，可能得到q也可能得到－q。公式4.40的直观理解就是上面的图。下面的公式代表两个四元数数对一个p进行变化。

四元数和矩阵的转化。因为在硬件上使用矩阵要比使用四元数计算的更快，所以可以在应用层面上使用四元数，但是在计算层面上使用矩阵。他们之间的转化为：

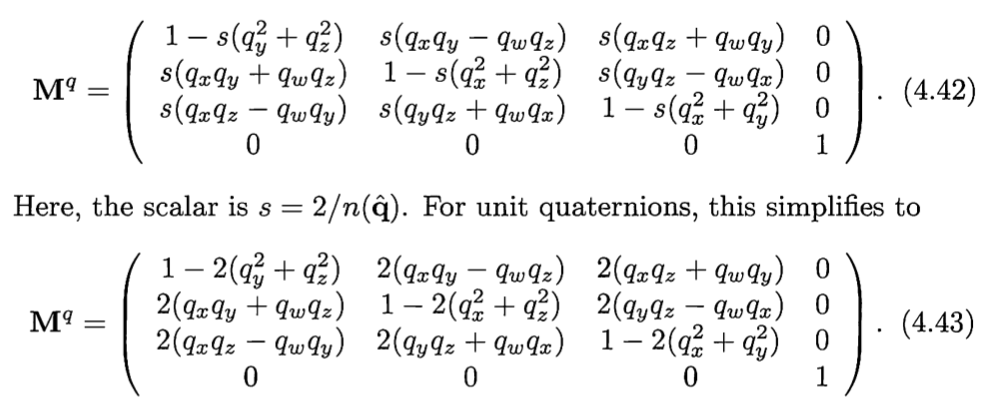
但是在应用层面上要使用四元数时，又要从矩阵转化成四元数。通过观察，可以看到以下等式

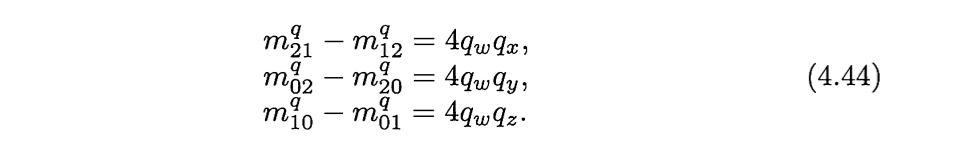
　  如果直到qw , qx , qy , qz中的任何一个，都可以计算出另外三个。通过观察可以知道如下等式：

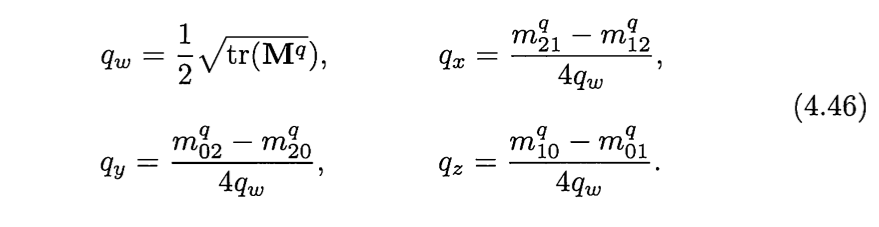
　　其中tr(M^q)的意思时矩阵的迹，也就是矩阵对角线的和。在计算过程中，我们知道应该尽量避免除以一个比较小的数字。所以4.46不一定时最好的算法。通过以下比较

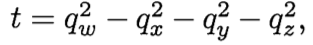
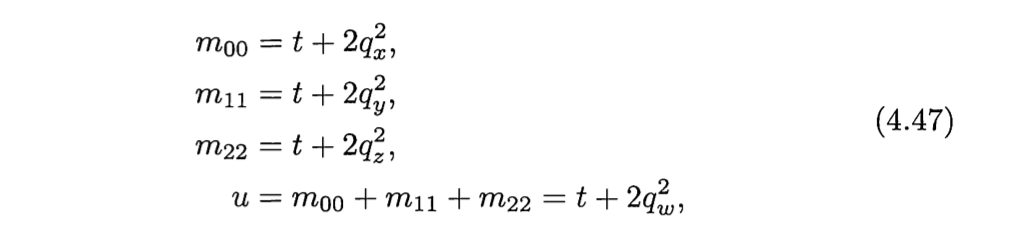
　　可知，通过比较矩阵的几个元素和u的大小就可以知道q_x q_y q_z q_w 的大小关系。如果q_w 最大，那么直接使用4.46就可以。如果不是，那么可以使用如下方法，算出最大的那个元素值，然后决定使用4.44时那个元素作为分母。