【比赛】HNOI2018 道路

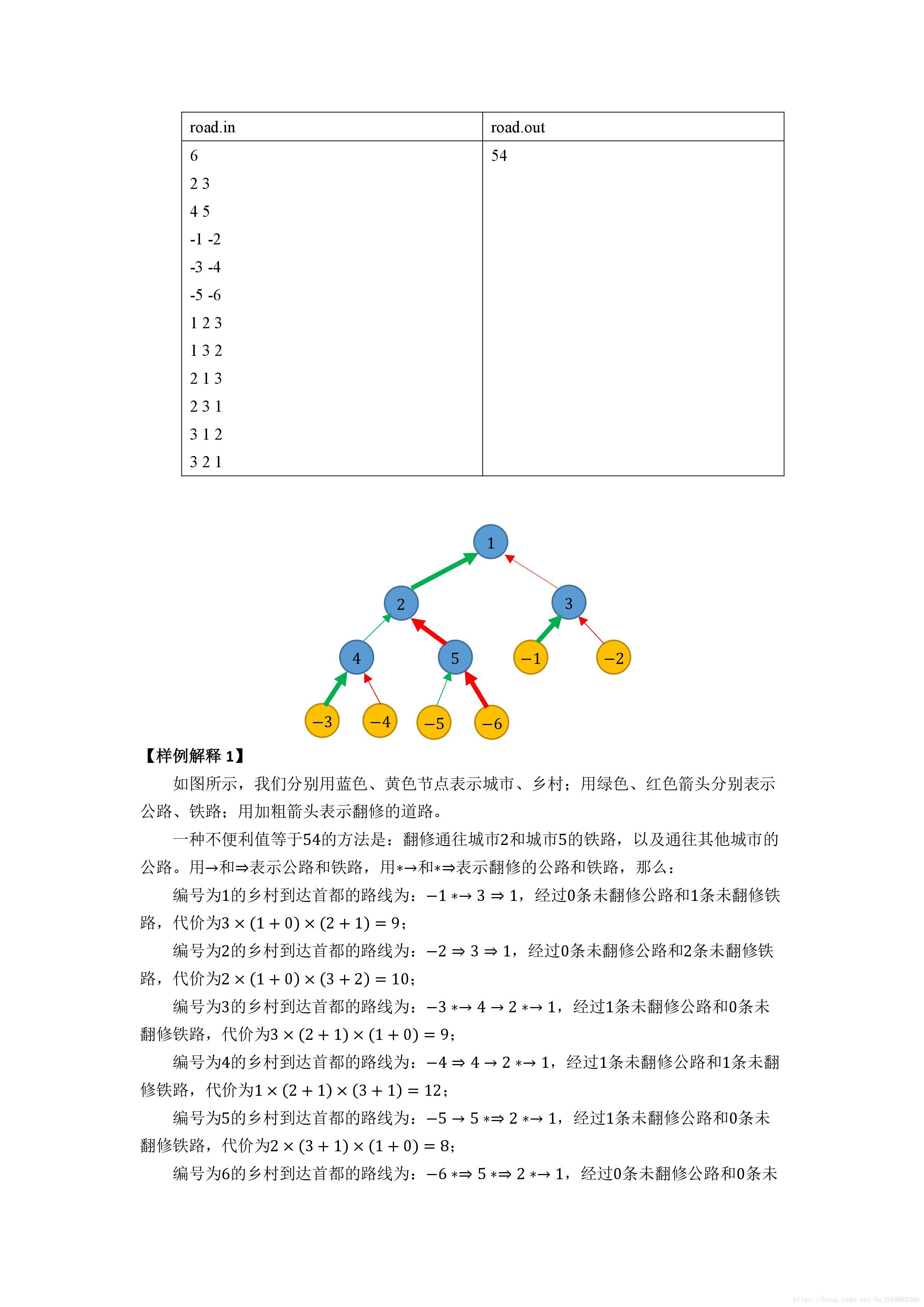
这题很考思维啊，考验我们能否快速从省选难度跳转到普及难度

考试的时候真的想得太多，觉得省选不可能这么简单吧，然后就打脸

设 \(f[i][j][x]\) 表示从根到 \(x\) 号点，有 \(i\) 条公路未修，有 \(j\) 条铁路未修的最小答案

然后？

直接转移啊

对于乡村：\(f[i][j][x]=c[x]*(a[x]+i)*(b[x]+j)\)

对于城市：\(f[i][j][x]=min\{f[i+1][j][ls]+f[i][j][rs],f[i][j][ls]+f[i][j+1][rs]\}\)

然后应对卡空间，另类滚动一下就好了

#include<bits/stdc++.h>
#define ui unsigned int
#define ll long long
#define db double
#define ld long double
#define ull unsigned long long
const int MAXN=20001;
int n,nxt[MAXN][2],stack[110],cnt,pt[MAXN<<1];
ll f[45][45][110],inf=0x3f3f3f3f3f3f3f3f;
struct data{
	int a,b,c;
};
data cty[MAXN];
template<typename T> inline void read(T &x)
{
	T data=0,w=1;
	char ch=0;
	while(ch!='-'&&(ch<'0'||ch>'9'))ch=getchar();
	if(ch=='-')w=-1,ch=getchar();
	while(ch>='0'&&ch<='9')data=((T)data<<3)+((T)data<<1)+(ch^'0'),ch=getchar();
	x=data*w;
}
template<typename T> inline void write(T x,char ch='\0')
{
	if(x<0)putchar('-'),x=-x;
	if(x>9)write(x/10);
	putchar(x%10+'0');
	if(ch!='\0')putchar(ch);
}
template<typename T> inline void chkmin(T &x,T y){x=(y<x?y:x);}
template<typename T> inline void chkmax(T &x,T y){x=(y>x?y:x);}
template<typename T> inline T min(T x,T y){return x<y?x:y;}
template<typename T> inline T max(T x,T y){return x>y?x:y;}
inline void dfs(int x,int Mi,int Mj)
{
	stack[++cnt]=x;pt[x]=cnt;
	if(x>n-1)
		for(register int i=0;i<=Mi;++i)
			for(register int j=0;j<=Mj;++j)f[i][j][pt[x]]=1ll*cty[x-n+1].c*(cty[x-n+1].a+i)*(cty[x-n+1].b+j);
	else
	{
		dfs(nxt[x][0],Mi+1,Mj);dfs(nxt[x][1],Mi,Mj+1);
		for(register int i=0;i<=Mi;++i)
			for(register int j=0;j<=Mj;++j)f[i][j][pt[x]]=min(f[i+1][j][pt[nxt[x][0]]]+f[i][j][pt[nxt[x][1]]],f[i][j][pt[nxt[x][0]]]+f[i][j+1][pt[nxt[x][1]]]);
		cnt-=2;
	}
}
int main()
{
	freopen("road.in","r",stdin);
	freopen("road.out","w",stdout);
	read(n);
	for(register int i=1;i<n;++i)
	{
		int x,y;
		read(x);read(y);
		if(x<0)x=-x+n-1;if(y<0)y=-y+n-1;
		nxt[i][0]=x;nxt[i][1]=y;
	}
	for(register int i=1;i<=n;++i)read(cty[i].a),read(cty[i].b),read(cty[i].c);
	dfs(1,0,0);
	write(f[0][0][pt[1]],'\n');
	return 0;
}