【BZOJ3240】【UOJ#124】【NOI2013】矩阵游戏

终于看懂一道题QAQ然而NOI都是这种难度题怎么玩QAQ

原题：

婷婷是个喜欢矩阵的小朋友,有一天她想用电脑生成一个巨大的n行m列的矩阵(你不用担心她如何存储)。她生成的这个矩阵满足一个神奇的性质：若用F[i][j]来表示矩阵中第i行第j列的元素，则F[i][j]满足下面的递推式:

F[1][1]=1
F[i,j]=a*F[i][j-1]+b (j!=1)
F[i,1]=c*F[i-1][m]+d (i!=1)
递推式中a,b,c,d都是给定的常数。

现在婷婷想知道F[n][m]的值是多少,请你帮助她。由于最终结果可能很大，你只需要输出F[n][m]除以1,000,000,007的余数。

1<=N,M<=10^1000 000,a<=a,b,c,d<=10^9

恩显然数论

数论嘛，直接推公式

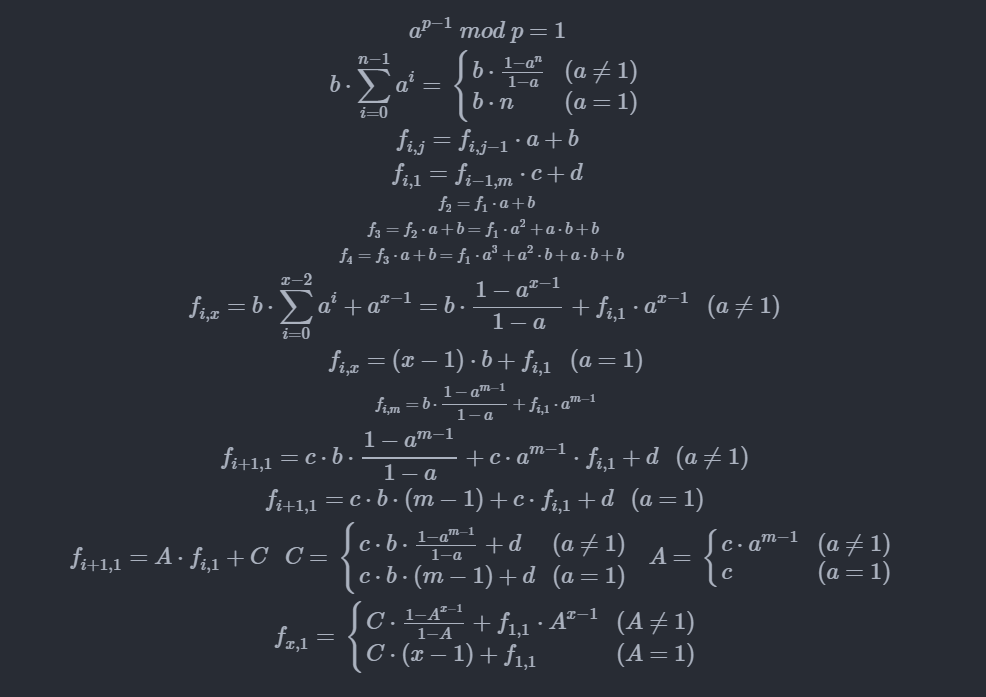
然后就可以一步算出来f[n][1]，然后再一步算出来f[n][m]即可

推推公式或许有奇迹hhh

（然而那个把f[i][1]推到f[i+1][1]的公式转化成C*（1-A^(x-1))/(1-A)+f[1][1]*A^(x-1)的形式似乎真的不好想出来QAQ

实现有许多细节，尤其是处理A是否等于1的时候容易写错

NOI都是这种难度的题怎么玩嘛QAQ

代码：

 #include<iostream>
 #include<cstdio>
 #include<algorithm>
 #include<cstring>
 #include<cmath>
 using namespace std;
 #define ll long long
 const int mo=(int)1e9+;
 int rd(){int z=,mk=;  char ch=getchar();
     while(ch<''||ch>''){if(ch=='-')mk=-;  ch=getchar();}
     while(ch>=''&&ch<=''){z=(z<<)+(z<<)+ch-'';  ch=getchar();}
     return z*mk;
 }
 char n[],m[];
 ll na=,nb=,ma=,mb=,a,b,c,d;  ll C,A;
 ll qcp(ll x,ll y){
     ll z=,bs=x;
     while(y){  if(y&)  z=(z*bs)%mo;  bs=(bs*bs)%mo;  y>>=;}
     return z;
 }
 ll x_1(ll x){  return qcp(x,mo-);}
 int main(){freopen("ddd.in","r",stdin);
     scanf("%s%s",n,m);
     int ln=strlen(n),lm=strlen(m);
     for(int i=;i<ln;++i)  na=(na*+n[i]-'')%mo,nb=(nb*+n[i]-'')%(mo-);
     for(int i=;i<lm;++i)  ma=(ma*+m[i]-'')%mo,mb=(mb*+m[i]-'')%(mo-);
     if(na==)  na=mo;  if(ma==)  ma=mo;  if(nb==)  nb=mo-;  if(mb==)  mb=mo-;
     cin>>a>>b>>c>>d;
     if(a!=)  C=(c*b%mo*(qcp(a,(mb-))-)%mo*x_1(a-)%mo+d)%mo,A=c*qcp(a,(mb-))%mo;
     else  C=(c*b%mo*(ma-)%mo+d)%mo,A=c;
     ll tmp;
     if(A!=)  tmp=(C*(qcp(A,(nb-))-)%mo*x_1(A-)%mo+qcp(A,(nb-)))%mo;
     else  tmp=(C*(na-)%mo+)%mo;
     ll ans;
     if(a!=)  ans=(b*(qcp(a,(mb-))-)%mo*x_1(a-)%mo+tmp*qcp(a,(mb-))%mo)%mo;
     else  ans=((ma-)*b%mo+tmp)%mo;
     cout<<(ans%mo+mo)%mo<<endl;
     //cout<<C<<" "<<A<<" "<<tmp<<endl;
     return ;
 }