[Bayes] Multinomials and Dirichlet distribution

From: https://www.cs.cmu.edu/~scohen/psnlp-lecture6.pdf 不错的PPT，图示很好。

---

伯努利分布 和 多项式分布

Binomial Distribution的共轭先验Beta Distribution。

贝塔分布的范围符合色子的每一面的概率理解。

同理：

Multinomials Distribution的共轭先验Dirichlet Distribution。

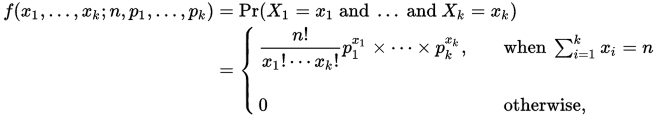
Ref: https://docs.scipy.org/doc/numpy/reference/generated/numpy.random.multinomial.html

>>> np.random.multinomial(20, [1/6.]*6, size=2)　　# 做size=2次实验，一次是20次抛投
array([[3, 4, 3, 3, 4, 3],　　# 第一次实验的结果：第一面出现了3次，第二面出现了4次，etc.
       [2, 4, 3, 4, 0, 7]])  # 第二次实验同理。

没法做图表示，维度太高了，大于了三维。第三维要留下来表示Pr。

---

狄利克雷分布：

Dirichlet分布可以看做是分布之上的分布。如何理解这句话，我们可以先举个例子：

• 假设我们有一个骰子，其有六面，分别为{1,2,3,4,5,6}。现在我们做了10000次投掷的实验，得到的实验结果是六面分别出现了{2000,2000,2000,2000,1000,1000}次，如果用每一面出现的次数与试验总数的比值估计这个面出现的概率，则我们得到六面出现的概率，分别为{0.2,0.2,0.2,0.2,0.1,0.1}。
• 我们想要做10000次试验，每次试验中我们都投掷骰子10000次。我们想知道，出现这样的情况使得我们认为，骰子六面出现概率为{0.2,0.2,0.2,0.2,0.1,0.1}的概率是多少（说不定下次试验统计得到的概率为{0.1, 0.1, 0.2, 0.2, 0.2, 0.2}这样了）。

这样我们就在思考骰子六面出现概率分布这样的分布之上的分布。

而这样一个分布就是Dirichlet分布。

• xi 代表每一面的概率。
• 阿尔法是参数向量。
• 以下B函数是为了归一化！
• 可以看出，每一个结果：(x1, x2... xn)都会相应地给出一个概率！

伽玛函数（Gamma函数），也叫欧拉第二积分，是阶乘函数在实数与复数上扩展的一类函数。

与之有密切联系的函数是贝塔函数（Beta函数），也叫第一类欧拉积分。可以用来快速计算同伽马函数形式相类似的积分。

长得比较诡异。

Ref: https://docs.scipy.org/doc/numpy/reference/generated/numpy.random.dirichlet.html

一个三维的向量，随机抽取一个。每一维代表一个面的概率。

>>> s = np.random.dirichlet((10, 5, 3), 20)
>>> s
array([[ 0.52347182,  0.44608268,  0.0304455 ],
       [ 0.55583862,  0.35281005,  0.09135134],
       [ 0.49311777,  0.32315067,  0.18373157],
       [ 0.70968695,  0.22268722,  0.06762583],
       [ 0.60323203,  0.26006693,  0.13670104],
       [ 0.69403583,  0.21325088,  0.09271329],
       [ 0.53413248,  0.23281167,  0.23305585],
       [ 0.62858314,  0.18519664,  0.18622022],
       [ 0.52497339,  0.20176998,  0.27325663],
       [ 0.47283724,  0.39204232,  0.13512045],
       [ 0.66621238,  0.24627779,  0.08750983],
       [ 0.43605494,  0.46696468,  0.09698038],
       [ 0.41539035,  0.37153284,  0.21307682],
       [ 0.85737303,  0.11670994,  0.02591703],
       [ 0.53161652,  0.28426861,  0.18411488],
       [ 0.55155807,  0.16826288,  0.28017905],
       [ 0.45716724,  0.33973818,  0.20309457],
       [ 0.45320309,  0.26896615,  0.27783076],
       [ 0.80522192,  0.10022979,  0.09454829],
       [ 0.45790405,  0.42998929,  0.11210666]])

可见，参数某个比较大时，会出现一个高的相对稳定的概率峰值。

>>> s = np.random.dirichlet((10, 1, 1), 20)
>>> s
array([[ 0.8557684 ,  0.09807372,  0.04615788],
       [ 0.83456424,  0.03670665,  0.12872911],
       [ 0.73520196,  0.2017358 ,  0.06306224],
       [ 0.73759042,  0.18157695,  0.08083263],
       [ 0.89338746,  0.00237974,  0.1042328 ],
       [ 0.93393029,  0.01373741,  0.0523323 ],
       [ 0.96453549,  0.02562915,  0.00983536],
       [ 0.90688036,  0.02557378,  0.06754587],
       [ 0.96455728,  0.02084742,  0.01459531],
       [ 0.82136655,  0.07921894,  0.09941451],
       [ 0.78585535,  0.00286702,  0.21127763],
       [ 0.91597604,  0.0276861 ,  0.05633787],
       [ 0.90984927,  0.04313451,  0.04701622],
       [ 0.81386422,  0.08610383,  0.10003195],
       [ 0.92675313,  0.06861093,  0.00463594],
       [ 0.98362761,  0.00299704,  0.01337535],
       [ 0.90807198,  0.02043488,  0.07149314],
       [ 0.90418455,  0.07209613,  0.02371932],
       [ 0.9630694 ,  0.00459631,  0.03233429],
       [ 0.65105053,  0.05350025,  0.29544922]])

阿尔法和小一点，则less peaked：出现了些许不稳定，某一个Pr的垄断性不是特别强。

>>> s = np.random.dirichlet((5, 1, 1), 20)
>>> s
array([[ 0.7373676 ,  0.17431797,  0.08831443],
       [ 0.8022481 ,  0.02474368,  0.17300822],
       [ 0.90968516,  0.06022567,  0.03008917],
       [ 0.9011515 ,  0.02337192,  0.07547658],
       [ 0.98846934,  0.00932316,  0.0022075 ],
       [ 0.66322211,  0.24058232,  0.09619557],
       [ 0.86661876,  0.0542239 ,  0.07915735],
       [ 0.48498043,  0.25048716,  0.26453241],
       [ 0.79705359,  0.16538074,  0.03756567],
       [ 0.68670999,  0.17210651,  0.1411835 ],
       [ 0.65227745,  0.20477286,  0.1429497 ],
       [ 0.73701086,  0.15733187,  0.10565728],
       [ 0.68017492,  0.04459314,  0.27523195],
       [ 0.50579841,  0.42922063,  0.06498096],
       [ 0.71188347,  0.13582756,  0.15228897],
       [ 0.69952146,  0.08344366,  0.21703488],
       [ 0.39333132,  0.49440346,  0.11226522],
       [ 0.47531785,  0.21319548,  0.31148667],
       [ 0.67575678,  0.25481807,  0.06942515],
       [ 0.83958139,  0.08429426,  0.07612435]])

共轭，得到后验如下：