PCA主成份分析学习记要

前言

主成份分析，简写为PCA（Principle Component Analysis）。用于提取矩阵中的最主要成分，剔除冗余数据，同时降低数据纬度。现实世界中的数据可能是多种因数叠加的结果，如果这些因数是线性叠加，PCA就可以通过线性转化，还原这种叠加，找到最原始的数据源。

PCA原理

P.S: 下面的内容需要一定线性代数基础，如果只想了解如何在R中使用，可以跳过此节

本质上来讲，PCA主要是找到一个线性转换矩阵P，作用在矩阵X（X的列向量是一条记录，行向量是一个feature）上，使其转换（或称之为投影，投影可以使用矩阵形式表示）到一个新的空间中，得到矩阵Y。目的是使得Y的协方差矩阵具有如下特点：

1） 对角线元素重左上角到右下角降序排列

2） 非对角线元素全部为0

为什么要这样达到这个目的呢？

对角线上的元素是Y的行向量的方差，非对角线上的元素是协方差。方差越大，表示保留的信息越多越重要；协方差越小，表示相关性越低，冗余性越小。这个也是PCA的主要目的。

下面形式的描述PCA的原理

矩阵X，纬度为m*n，m是变量个数，n是数据数量，处理之前需要对X的行向量做均值化，也就是每一个元素减去行均值，为了简化方差和协方差的计算。令Y=PX，使得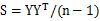是对角矩阵，且对角线上的值从大到小排列。

展开S，如下所示：

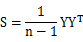
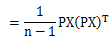
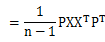
令A=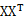，很容易证明A是对称矩阵，那么实对称均值的对角化在线性代数中是很成熟的技术，则有A=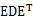,其中E是标准正交矩阵，带入上面公式

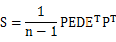
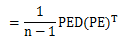
令，则

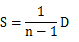
可以知道D中的每个元素其实就是A的特征值，而E中的向量就是特征向量经过正交化后的得到的标准正交基。让后根据A的特征值的大小降序排列。并对应排列E中向量的顺序。

PCA in R

R中内置两种PCA的实现，prcomp和princomp。前者采用SVD实现，后者采用上面的实对称矩阵对角化方式实现，两种的接口类似，只是前者的参数稍微多一些，下面的列子采用prcomp。

示例1：如何使用PCA

# 传感器坐标
recorders = data.frame("X" = c(0,0,1,1), "Y" = c(0,1,1,0) , row.names=c("A","B","C","D"))
# 光源坐标
locs = data.frame("X" = c(.3, .5), "Y" = c(.2, .8))
# 光源的发光强度时间序列
intensities = data.frame("sine" = sin(0:99*(pi/10))+1.2,
                          "cosine" = .7*cos(0:99*(pi/15))+.9)

# 传感器与光源的距离
dists = matrix(nrow = dim(locs)[1], ncol = dim(recorders)[1],
               dimnames = list(NULL, row.names(recorders)))
for (i in 1:dim(dists)[2]) {
    dists[, i] = sqrt((locs$X-recorders$X[i])^2+(locs$Y-recorders$Y[i])^2)
}

# 传感器记录的光源强度数据
set.seed(500)
recorded.data = data.frame(jitter(as.matrix(intensities)%*%as.matrix(exp(-2*dists)), amount = 0))

# 直观的感受一下传感器数据
plot(recorded.data)
round(cor(recorded.data), 2)
plot.ts(recorded.data)

# PCA原理1: 高相关性可能具有高度重复
# PCA原理2: 最重要的因数是那些具有最大方差的数据

# 手动执行PCA
Xoriginal = t(as.matrix(recorded.data))

# 中心化每个变量数据，以便每一行的均值为0
rm = rowMeans(Xoriginal)
X = Xoriginal - matrix(rep(rm, dim(Xoriginal)[2]), nrow = dim(Xoriginal)[1])

# 计算转换矩阵P
A = X %*% t(X)
E = eigen(A, symmetric = TRUE)
P = t(E$vectors)

newdata = P %*% X
sdev = sqrt(diag((P %*% A %*% t(P))/(dim(X)[2]-1)))

# 使用R内置PCA函数princomp
pr = princomp(recorded.data)
pr$sdev
pr$center

# 使用R内置PCA函数prcomp，采用SVD算法
pr = prcomp(recorded.data)
pr
plot(pr)
barplot(pr$sdev/pr$sdev[1])
pr2 = prcomp(recorded.data, tol = .1)
plot.ts(pr2$x)
par(mfrow = c(3,1))
windows(); plot.ts(intensities)
windows(); plot.ts(recorded.data)
windows(); plot.ts(cbind(-1*pr2$x[,1], pr2$x[,2]))
par(mfrow = c(1,1))

# 重构原始数据
od = pr$x %*% t(pr$rotation)
od2 = pr2$x %*% t(pr2$rotation)
windows(); plot.ts(recorded.data)
windows(); plot.ts(od)

此例子够着了两个光源数据，然后采用手动PCA算法和R内置PCA算法演示PCA，最后使用PCA的结果还原数据，演示PCA压缩数据。更具体的说明，可以参考这篇文章[2]

示例2：PCA简化数据

library("DMwR") # install.packages("DMwR")
cv.demo <- function(form, train, test, ...) {
    require(tree)
    model <- tree(form, train, ...)
    preds <- predict(model, test, type = 'class')
    class.eval(resp(form, test), preds)

}

# PCA建模1
pr <- prcomp(iris[-5])
new.data <- cbind(pr$x,iris[5])
eval.res <- crossValidation(learner('cv.demo',pars=list()),
                            dataset(Species ~ ., new.data),
                            cvSettings(1,10,1234))
summary(eval.res)

# PCA建模2
plot(pr) # 保留前3主成分
new.data2 <- cbind(pr$x[,1:3], iris[5])
eval.res <- crossValidation(learner('cv.demo',pars=list()),
                            dataset(Species ~ ., new.data2),
                            cvSettings(1,10,1234))
summary(eval.res)

# 直接建模
eval.res <- crossValidation(learner('cv.demo',pars=list()),
                            dataset(Species ~ ., iris),
                            cvSettings(1,10,1234))

summary(eval.res)

执行上面代码，可以发现在使用iris数据处理PCA时，第一个主成份占比达到92.46%，前三个主成份的权重达到99.48%。后面使用前三个主成份预测的平均错误率为4.7%，比采用原始数据预测的错误率6%低。

PCA假设

1. 变量符合高斯分布（正太分布）

2. 变量之间的影响是线性的，也就是可以通过线性变化将数据还原成主要因数

3. 协方差最大的元素对应的转换向量越重要

4. 转换矩阵是正交的

PCA的整个推导过程都是遵循上面的四条假设，如果违反了这些假设，PCA可能作用不大，甚至有反作用，所以使用PCA时需要谨慎。

PCA最佳实践

1. 压缩数据，主成份一般在90%，95%和99%几档，根据实际需要选取
2. 加速模型建模，缩短时间（PCA处理后，建模，需要保留转换向量P，并用P处理预测数据）
3. 可视化，如果前两个或三个数据可以表示90%以上的成分，那么可以进行可视化
4. PCA处理数据之前需要去报每个列的均值为0（mean normalization），同时需要确保量纲相同(scaling)，否则数值较大的几个变量会占据主要成分。
5. 不要将PCA作为解决过拟合的方法，虽然使用PCA后，确实可以减少过拟合，但是原因可能是feature减少了。采用regulations缓解过拟合。
6. 设计ML系统时，不要一开始就期望使用PCA，提高模型性能。只有当所有非PCA方法无法达到效果时，在使用PCA。PCA处理数据时没有考虑到y，会损失部分有价值信息

参考资料

[1]       PCA维基百科

[2]       PCA R示例（英文）

[3]       PCA数学原理：深入浅出，值得一读

[4]       最后那幅宇宙图片的例子很形象

[5]       Google研究员Jon Shlens的PCA原理介绍论文（英文）

[6]       Week 8 in Machine Learning, by Andrew NG, Coursera