transformations 变换集合关系 仿射变换
http://groups.csail.mit.edu/graphics/classes/6.837/F03/lectures/04_transformations.ppt
https://groups.csail.mit.edu/graphics/classes/6.837/F03/lectures/
Maps points (x, y) in one coordinate system to points (x', y') in another coordinate system
x' = ax + by + c
y' = dx + ey + f
For example, IFS:


Can be combined
Are these operations invertible?
Yes, except scale = 0
恒等 平移 旋转 等比缩放
可逆,除非等比缩放系数为0
Classes of Transformations 变换分类
Rigid Body / Euclidean Transforms 刚体、欧式变换
Similitudes / Similarity Transforms 相似性变换
Linear 线性变换
Affine 放射
Projective 投影
保持不变量的对象
点点之间
距离
线线之间
角度
平行关系
保距变换
保角变换
平行变换
Rigid-Body / Euclidean Transforms
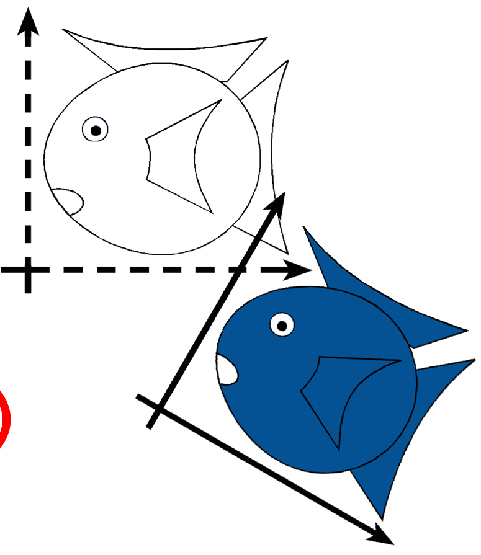
Preserves distances
Preserves angles
Rigid / Euclidean
Translation Identity Rotation
Similitudes / Similarity Transforms
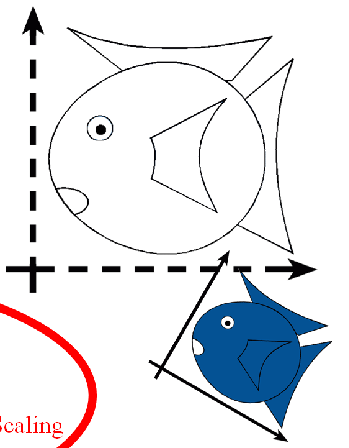
Linear Transformations
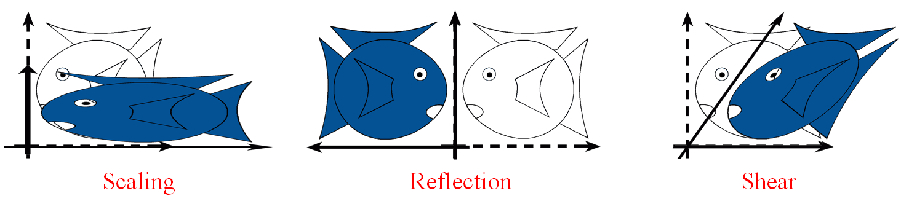
L(p + q) = L(p) + L(q)
L(ap) = a L(p)
shear
vt. 剪;修剪;剥夺
vi. 剪;剪切;修剪
切力 切变
Affine Transformations
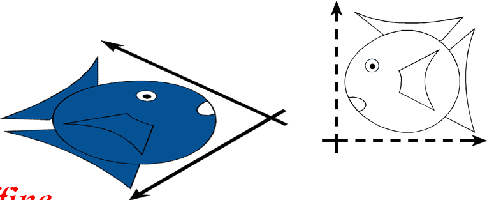
Projective Transformations
preserves lines

Representing Transformations 变换的表示
Combining Transformations 变换的联合
Change of Orthonormal Basis 改变正交基
How are Transforms Represented?
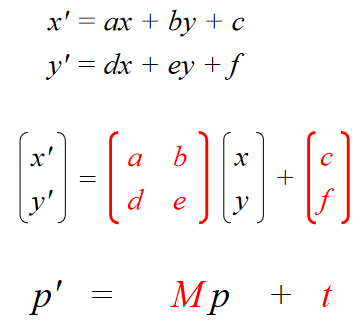
Homogeneous Coordinates 齐次坐标
Add an extra dimension
in 2D, we use 3 x 3 matrices
in 3D, we use 4 x 4 matrices
Each point has an extra value, w

Most of the time w = 1, and we can ignore it
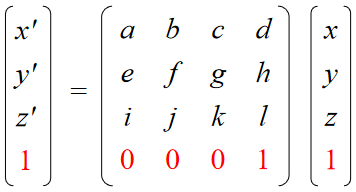
If we multiply a homogeneous coordinate by an affine matrix, w is unchanged
如果通过仿射矩阵来乘齐次坐标系,则w不变
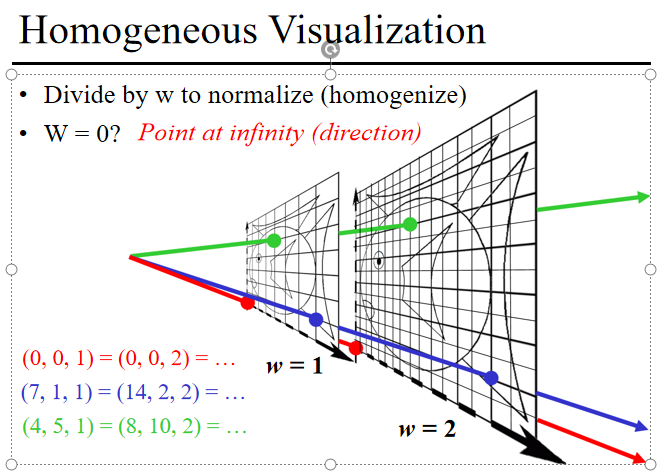
Divide by w to normalize (homogenize)
W = 0? Point at infinity (direction)
https://en.wikipedia.org/wiki/Affine_transformation


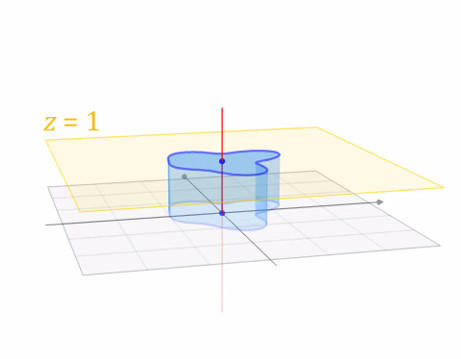
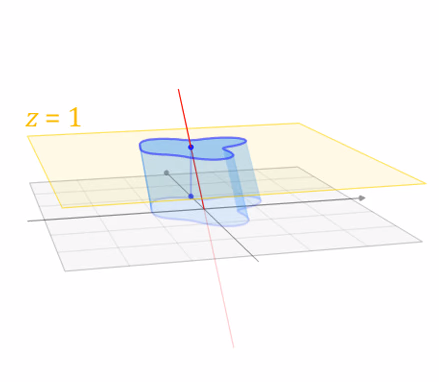
Translate (tx, ty, tz)
Why bother with the extra dimension? Because now translations can be encoded in the matrix!
Translate(c,0,0)
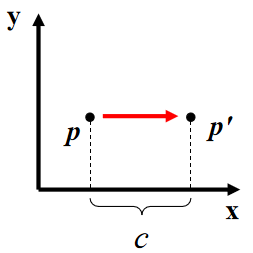
Scale (sx, sy, sz)
Isotropic (uniform) scaling: sx = sy = sz
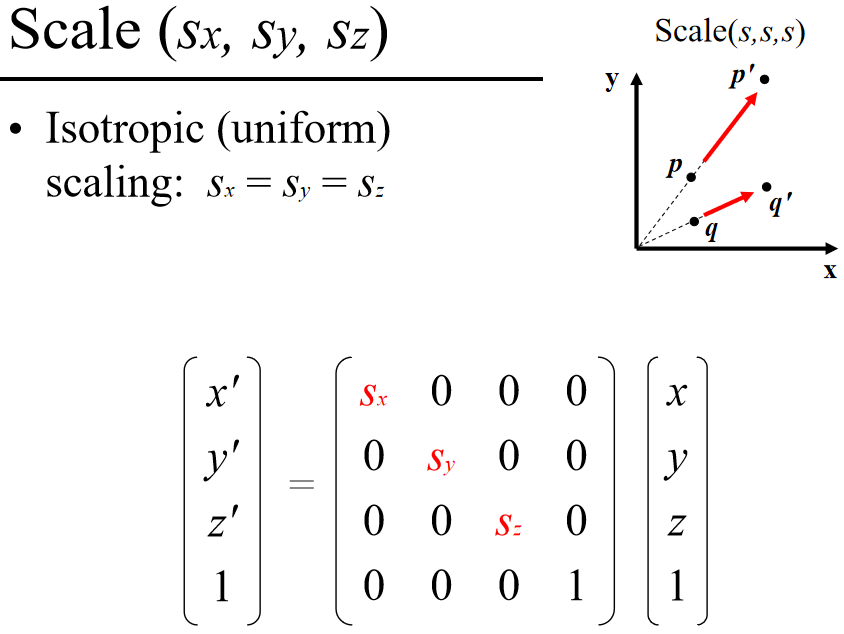
扩展
旋转
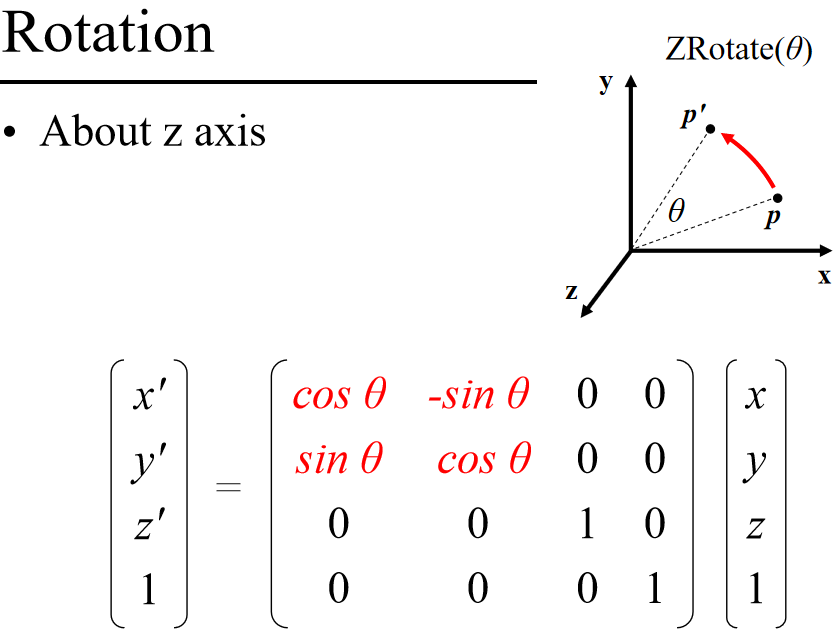
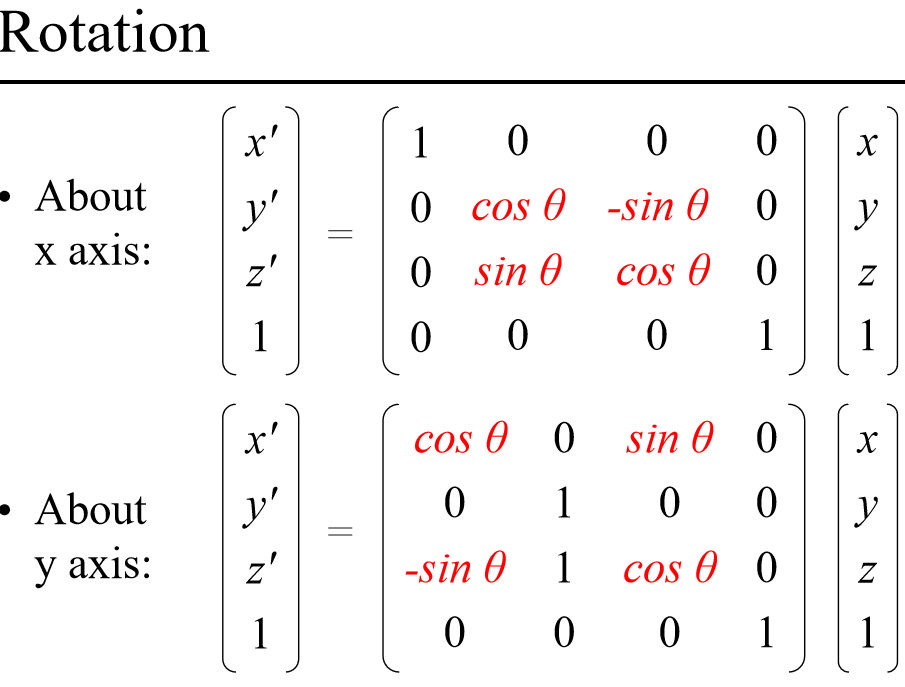
关于不同坐标轴旋转
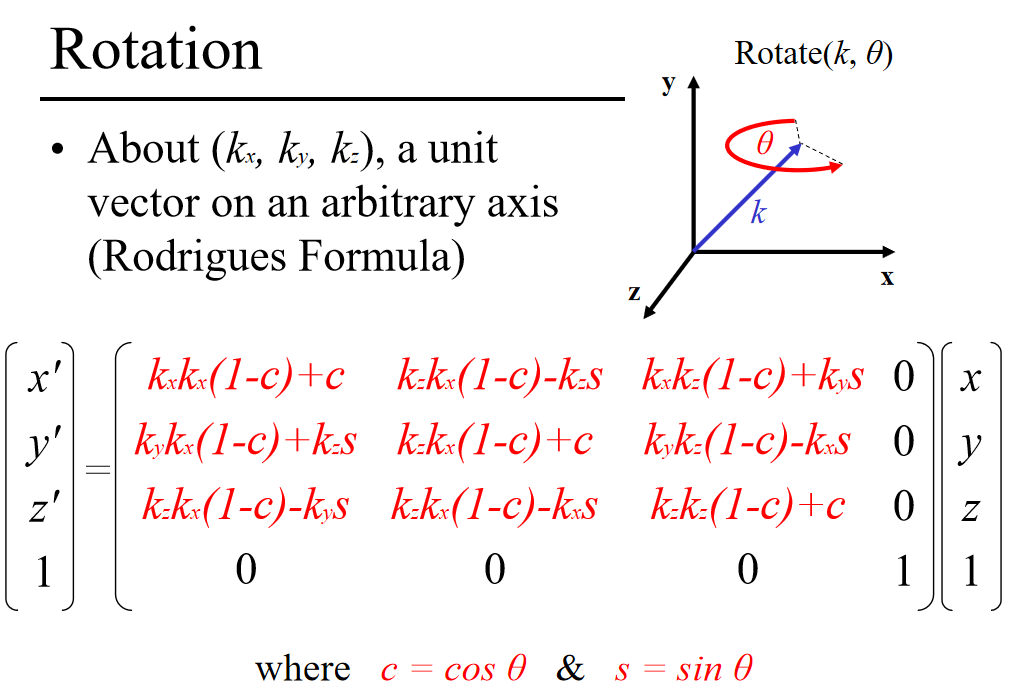
About (kx, ky, kz), a unit vector on an arbitrary axis(Rodrigues Formula)
How are transforms combined?
Scale then Translate

Use matrix multiplication: p' = T ( S p ) = TS p
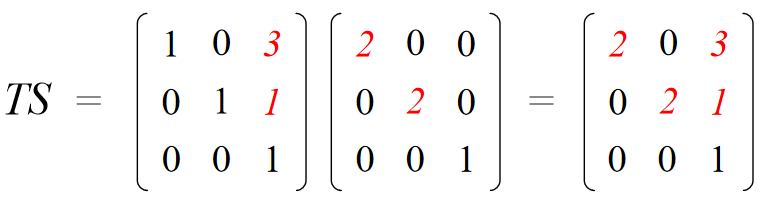
Caution: matrix multiplication is NOT commutative!
矩阵相乘不可以交换
Non-commutative Composition
Scale then Translate: p' = T ( S p ) = TS p

Translate then Scale: p' = S ( T p ) = ST p



Review of Dot Product
点乘
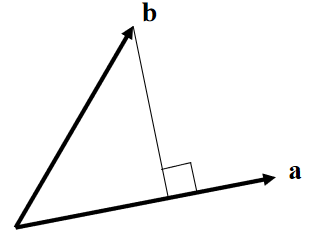
Change of Orthonormal Basis
Given: coordinate frames
xyz and uvn
point p = (x,y,z)
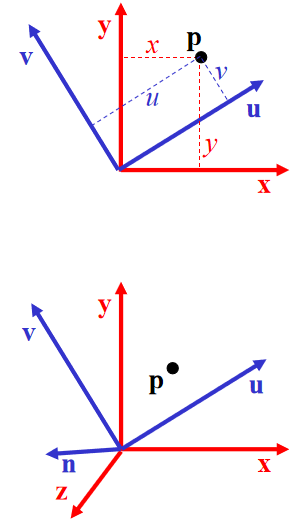
Find: p = (u,v,n)
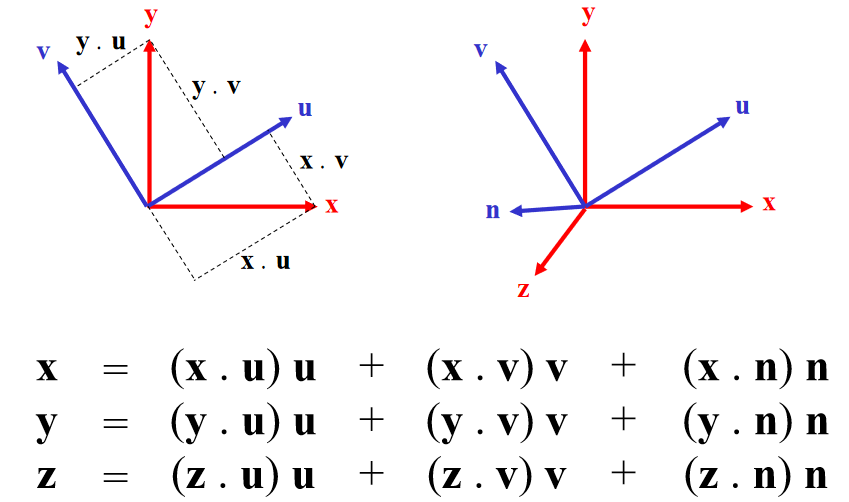
Substitute into equation for p:
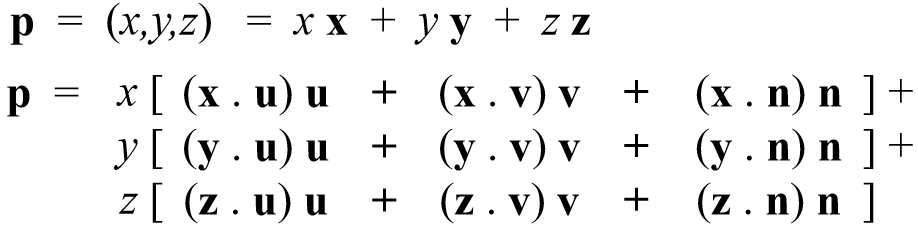
Rewrite:
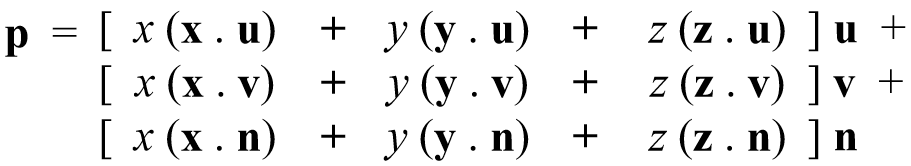
p = (u,v,n) = u u + v v + n n
Expressed in uvn basis:

In matrix form:
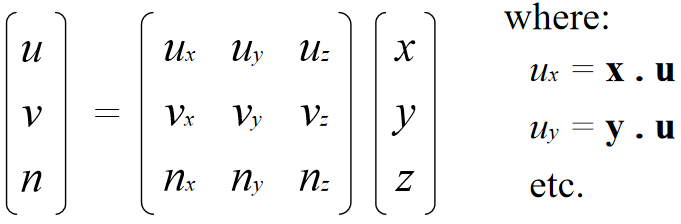
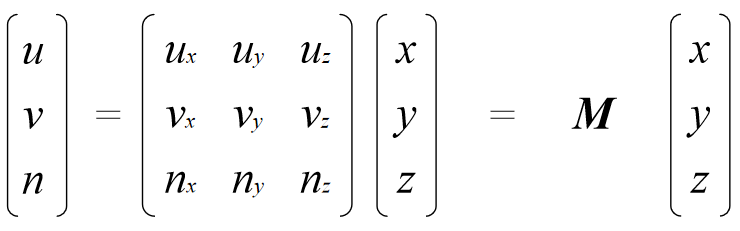
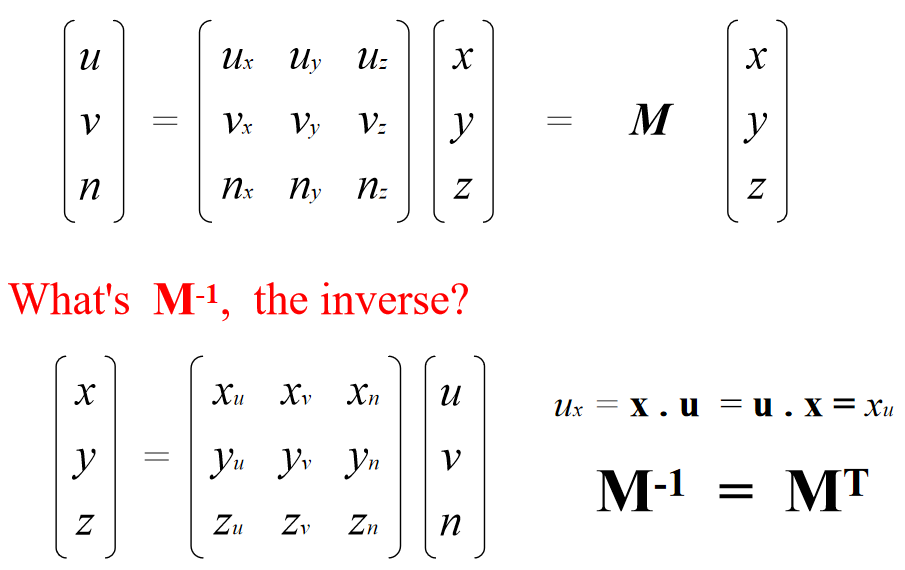
transformations 变换集合关系 仿射变换的更多相关文章
- MongoDB学习笔记~使用原生语句实现三层集合关系的更新
回到目录 MongoDB的文档型数据结构使得它在存储数据上很像JSON,在可读性方面很强,然而这种复杂的结构在update时相对麻烦一些,而对于官方给出的文档说的也不够细致,有些东西也是模棱两可的态度 ...
- python 全栈开发,Day7(元组转换,列表以及字典的坑,集合,关系测试,深浅copy,编码补充)
一.元组转换 数字 tu = (1) tu1 = (1,) print(tu,type(tu)) print(tu1,type(tu1)) 执行输出: 1 <class 'int'>(1, ...
- java基础笔试题二(集合关系)
知识点:java集合继承关系(Collection,Map) 1.集合框架体系图 2.java的集合层次 来自博客(http://blog.csdn.net/stubbornaccepted/arti ...
- day14 Python集合关系运算交,差,并集
low逼写法,没用集合 python_1 = ['charon','pluto','ran'] linux_1 = ['ran','xuexue','ting'] python_and_linux = ...
- LaTex中集合关系的表示
集合的大括号: \{ ... \} \(\{ ... \}\) 集合中的"|": \mid \(\mid\) 属于: \in \(\in\) 不属于: \not\in \(\not ...
- java集合的中的集合关系实现或继承关系图
放在这儿一目了然.
- Java - 集合之间的关系和区别
1.Java集合关系图: 2.List.Map.Set区别: ① List ArrayList LinkedList Vector Advantage Search Insert.Delete Syn ...
- opencv中的仿射变换
什么是仿射变换? 原理:1.一个任意的仿射变换都能表示为 乘以一个矩阵(线性变换) 接着再 加上一个向量(平移) 2.综上所述,我们能够用仿射变换来表示: 1)旋转(线性变换) 2)平移(向量加) 3 ...
- 2D射影几何和变换
阅读<计算机视觉中的多视图集合> 2D射影几何和变换 2D射影平面 本章的关键是理解线和点的对偶性.从射影平面模型出发,IP^2^内的点(a, b ,c)由IP^3^空间中一条过原点的射线 ...
随机推荐
- 3D建模软件的选择(UG,Solidworks,ProE)
转自:3D建模软件的选择(UG,Solidworks,ProE) 自述 咱是一个码农,和web.软件.控制台打交道太多了,很想玩玩炫的东西,于是学了点点PS,结果发现完全没有美术细胞TT.最近有碰到对 ...
- Atitit xml框架类库选型 attilax总结
Atitit xml框架类库选型 attilax总结 1. 1. XML类库可以分成2大类.标准的.这些类库通常接口和实现都是分开的1 2. Jdom 和dom4j1 2.1. 5.1. jdom1 ...
- mxnet:基础知识和一个简单的示例
NDArray与NumPy的多维数组类似,但NDArray提供了更多的功能:GPU和CPU的异步计算:自动求导.这使得NDArray能更好地支持机器学习. 初始化 from mxnet import ...
- Spring Security 之Http Basic认证
使用Spring Security进行http Basic认证非常简单,直接配置即可使用,如下: <security:http> <security:http-basic>&l ...
- 转载——githup的提交
Github是管理软件开发的首选托管网站,12306的火车票插件一时让国内当时很多小白开发者(当然也包括我)认识到了这个网站.GitHub可以托管各种git库,并提供一个web界面,与 SourceF ...
- AD域部署使用bginfo软件
实验网络拓扑图: 实验目标: bginfo收集信息服务器通过bginfo软件收集每个域客户端信息录入到SQL server 2008数据库 bginfo软件官网下载地址: https://docs.m ...
- Ubuntu下Apache虚拟主机+反向代理
反向代理 就是通过一台代理服务器,让Internet用户可以访问到内部网络上的服务器 下图中192.168.0.4 可以理解带有2个网卡,一个是公网ip,一个是192.168.0.4 代理内外中的2个 ...
- 追踪go语言(golang)的新版本新特性【摘抄】
Go 2.0 新特性展望:详细 go2.0 会有什么新特性呢?下图是一个老外的调侃,他不希望发生这样的事情(please don't make it happen).我倒是希望其中一些实现,比如泛型和 ...
- (转) at&T语法格式 与 at&T - intel格式对比
原地址 示例: movl (%ebp), %eax, 等同于Intel格式中的 ] ,AT&T中,源操作数在左,目的操作数在右.“l”是Longword,相当于Intel格式中的dword p ...
- 【代码审计】大米CMS_V5.5.3 任意文件读取漏洞分析
0x00 环境准备 大米CMS官网:http://www.damicms.com 网站源码版本:大米CMS_V5.5.3试用版(更新时间:2017-04-15) 程序源码下载:http://www ...
