bzoj 2115 Xor - 线性基 - 贪心

题目传送门

　　这是个通往vjudge的虫洞

　　这是个通往bzoj的虫洞

题目大意

　　问点$1$到点$n$的最大异或路径。

　　因为重复走一条边后，它的贡献会被消去。所以这条路径中有贡献的边可以看成是一条$1$到$n$的简单路径加上若干个环。

　　因此可以找任意一条路径，然后找出所有环扔进线性基跑出最大异或和。

　　但是找出所有环可能会T掉，但是仔细画图发现，并不需要找出所有环，例如：

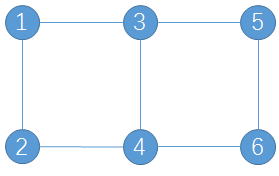
　　在上图中，你并不需找出所有的环，只用找出1 - 3 - 4 - 2和3 - 5 - 6 - 4这两个环，它们异或后就能得到环1 - 3 - 5 - 6 - 4 - 2。

　　至于找这个环，可以用dfs生成树来找。当出现返祖边的时候就意味着找到了一个环。

　　然后可以记一个异或的前缀和，这样就可以$O(1)$算出环上的边权的异或和。

　　对于任意一条路径得到的异或和如果为$s$，那么我们只需要考虑线性基的每一位上，如果异或上它，能够使答案变大，就异或上它。

　　因为线性基不能保证最大的异或和由之前扔进去的所有数得到，所以必须这么贪一下心。

　　这样的正确性显然。

Code

 /**
  * bzoj
  * Problem#2115
  * Accepted
  * Time: 740ms
  * Memory: 7040k
  */
 #include <bits/stdc++.h>
 #ifndef WIN32
 #define Auto "%lld"
 #else
 #define Auto "%I64d"
 #endif

 using namespace std;
 typedef bool boolean;

 #define ll long long

 typedef class LinearBasis {
     public:
         ll b[];

         LinearBasis() {    }

         void insert(ll x) {
             for (int i = ; ~i; i--) {
                 if (x & (1ll << i))    x ^= b[i];
                 if (x & (1ll << i)) {
                     b[i] = x;
                     for (int j = i - ; ~j; j--)
                         if (b[i] & (1ll << j))
                             b[i] ^= b[j];
                     for (int j = i + ; j <= ; j++)
                         if (b[j] & (1ll << i))
                             b[j] ^= b[i];
                     break;
                 }
             }
         }

         ll getAns(ll ans) {
             for (int i = ; i <= ; i++)
                 if ((ans ^ b[i]) > ans)
                         ans ^= b[i];
             return ans;
         }
 }LinearBasis;

 typedef class Edge {
     public:
         int end, next;
         ll w;

         Edge(int end = , int next = , ll w = ):end(end), next(next), w(w){    }
 }Edge;

 typedef class MapManager {
     public:
         int ce;
         int *h;
         Edge* es;

         MapManager() {    }
         MapManager(int n, int m):ce() {
             h = new int[(n + )];
             es = new Edge[(m + )];
             memset(h, , sizeof(int) * (n + ));
         }

         void addEdge(int u, int v, ll w) {
             es[++ce] = Edge(v, h[u], w);
             h[u] = ce;
         }

         Edge& operator [] (int p) {
             return es[p];
         }
 }MapManager;

 int n, m;
 ll *xs;
 MapManager g;
 LinearBasis lb;
 boolean *vis;

 inline void init() {
     scanf("%d%d", &n, &m);
     xs = new ll[(n + )];
     g = MapManager(n, m << );
     vis = new boolean[(n + )];
     ll w;
     for (int i = , u, v; i <= m; i++) {
         scanf("%d%d"Auto, &u, &v, &w);
         g.addEdge(u, v, w);
         g.addEdge(v, u, w);
     }
 } 

 void dfs(int p) {
     vis[p] = true;
     for (int i = g.h[p]; i; i = g[i].next) {
         int e = g[i].end;
         if (vis[e])
             lb.insert(xs[e] ^ xs[p] ^ g[i].w);
         else {
             xs[e] = xs[p] ^ g[i].w;
             dfs(e);
         }
     }
 }

 inline void solve() {
     memset(vis, false, sizeof(boolean) * (n + ));
     xs[] = ;
     dfs();
     printf(Auto"\n", lb.getAns(xs[n]));
 }

 int main() {
     init();
     solve();
     return ;
 }