清明 DAY２

数论

数论是研究整数性质的东西

---

---

也就是

lim   π（x）=x/ ln x

(x->无穷)

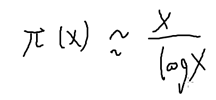
X越大越稀疏

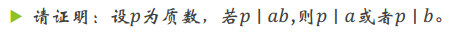
证明：

∵　p|ab

∴　ab有因子p

设 a=p₁^k1p₂^k2......p_r^kr

     b=q₁^t1q₂^t2......q_w^tw

那么ab= p₁^k1p₂^k2......p_r‑^kr q₁^t1q₂^t2......q_w‑^tw

∴　p₁----- q_w中一定有一个P，才能使p|ab

∴　p∈{ p₁p₂......p_r‑ q₁q₂......q_w}

∴　p|a　或者　p|b

---

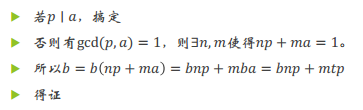
证明：

存在性：

假设存在N是最小的不满足质因数分解的数

　 N若是素数，N=N

∴　N是合数，存在p , N=p * N/p

　此时N/p也不可以质因数分解，那么N/p就比N小，与假设矛盾，证明存在性成立

唯一性：

假设存在N是最小的可以分解为两种不同方式的数

那么 N= p₁^k1p₂^k2......p_r^kr    （1）

　= q₁^t1q₂^t2......q_w^tw  （2）

∴　p₁| q₁^t1q₂^t2......q_w^tw          （3）

∴　p₁∈{ q₁^t1q₂^t2......q_w^tw }

∴　p₁| q₁或者p₁| q₂.....或者p₁| q_w

∵　p₁| q₁，p₁  q₁均为素数，

∴　p₁=q₁

设　r₁>=t₁

(1)(2)同时除以p₁^t1

∴　p₁^{r1 - t1}......=q₁⁰.......

∴　存在更小的可以分解为两种不同方式的数N/p₁^t1

　 与假设矛盾，证明唯一性成立

---

素数与筛法

---

证明：

ax+by=c 有整数解  =>  gcd(a,b)|c

(充分）             （必要）

充分性

设d=gcd(a,b)，那么d|a　,　d|b　,　则d|ax+by=c

必要性

gcd(a,b)|c  =>  ax+by=c 有整数解

x,y是整数，ax+by>0

只需证出min(ax+by)=gcd(a,b)即可

设d=gcd(a,b)   s=min(ax+by) s>0

a/s = q.....r

r = a - qs = a - q (ax+by) =(1-qx)a - qyb

为了保证s最小，那么r=0，所以s|a , 同理可得s|b , 所以，s|gcd(a,b)即s|d

s=ax+by=x(nd)+y(md)   =>  d|s

因为s|d， d|s

所以s=d

---

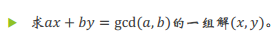
PS：ａ%ｂ＝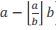

---

---

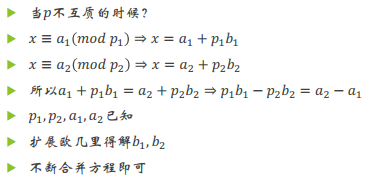
注意这里是对于p的逆元

代替乘法

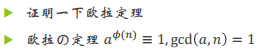
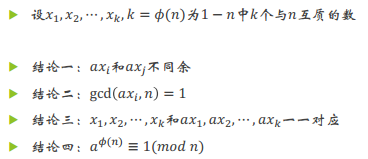
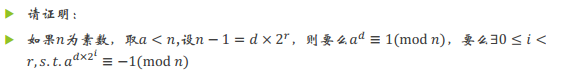
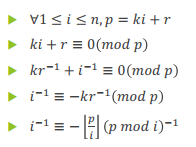
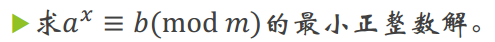
代码：

int size;

bool erfen(int x)
{
    int l=,r=size;
    while (l+!=r)
    {
        int m=(l+r)>>;
        if (z[m]>=x) r=m;
        else l=m;
    }
    return z[r]==x;
}

int bsgs(int a,int b,int p)
{
    size = sqrt(p);

    int nowv=;
    for (int i=;i<=size;i++)
    {
        nowv = (long long)nowv * a%p;
        z[i] = nowv;
        if (z[i] == b) return i;  //如果在列举第一行 已经找到了i，直接返回
    }
    sort(z+,z+size+);
    for (int i=;(i-)*size+ <= p;i++)
    {
        int y = (long long)b * kuaisumi(kuaisumi(a,size*(i-),p),p-,p);          //快速幂套快速幂    从后往前找，乘以逆元
        if (erfen(y))   //发现x在这一行，暴力枚举一下
        {
            for (int j=(i-)*size+;j<=i*size;j++)
                if (kuaisimi(a,j,p) == b) return j;
        }
    }
    return -;
}

---

---

数论函数

带入一个正整数，输出一个整数

f(x)=y

x是正整数，y是整数

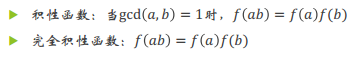
μ（x）

把x质因数分解：x=p₁^r1p₂^r2.......p_k^rk

令r = max { r₁ , r₂ , .... r_k }

1  ( x=1 )

μ（x）=    0  ( r >1 )

（-1）^k   ( r=1)

( k 表示 x 有k 个质因子)

举个栗子：

μ（4）=0；   μ（15）=1；   μ(1001)=-1

莫比乌斯函数是一个数论函数，它同时也是一个积性函数(i.e.μ(ab) =μ(a)μ(b), a,b互质)

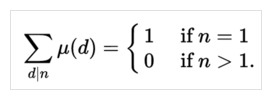
当n不等于1时，n所有因子的莫比乌斯函数值的和为0   （d是n的因子）

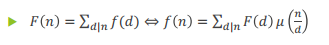
举个栗子：

F（6）= f (1) + f (2) + f（3）+ f (6);

f (6) = F（1）μ（6）+ F（2）μ（3）+ F（3）μ（2）+ F（6）μ（1）

证明一下：

∑  μ（d）F(n/d) = ∑   μ（d）  ∑    f (d^`)

d|n                        d|n           d^`|n/d

= ∑        ∑     μ（d）f (d^`)                        //交换求和符号   常用技能

d|n     d^`|n/d

= ∑        ∑      μ（d）f (d^`)

d^{`</sup>|n     d|n/d<sup>`}

= ∑    [  f (d^`)   ∑   μ（d） ]

d^{`</sup>|n            d|n/d<sup>`}

= f ( n )

大概就是这样

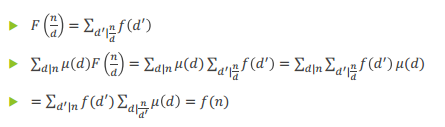
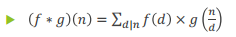
举个栗子：

设f(n)=n    g(x)=Φ（n）

那么（f*g）(12) = f(12)*g(1)  +  f(6)*g(2)  +  f(4)*g(3)

+ f(3)*g(4)  +  f(2)*g(6)  +  f(1)*g(12)

= 12*1  +  6*1  +  4*2  +  3*2  +  2*2  +  1*4

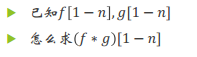
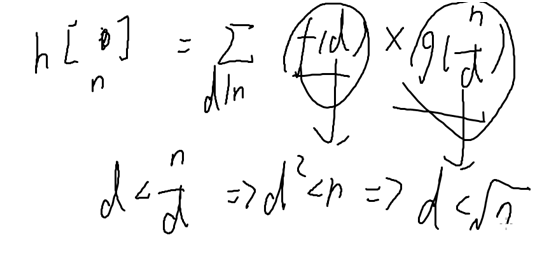
枚举较小的因子

不再枚举1-i的所有因子

而是枚举i的两个因子  降低复杂度

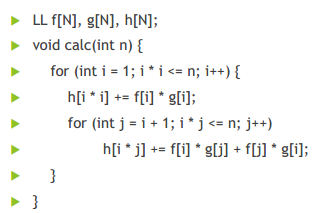
PS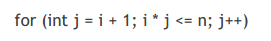：J是i的下一个因子

看题啦看题啦看题啦看题啦看题啦看题啦看题啦看题啦看题啦看题啦看题啦看题啦看题啦看题啦

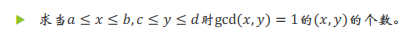
[ 1 <= x <= c , 1 <= y <= d ]

- [ 1 <= x <= a , 1 <= y <= d ]

- [ 1 <= x <= c , 1 <= y <= b ]

+ [ 1 <= x <= a , 1 <= y <= b ]

换个写法

如果括号里为真返回1 ，否则0

当然不可以从1-n,1-m都枚举一遍

n   m

∑   ∑ [ gcd ( i , j )=1 ]

i=1   j=1

n    m

= ∑   ∑     ∑   μ（d）

i=1   j=1  d|gcd( i,j )

只有当gcd为1 时候结果为1，否则为0；

很像莫比乌斯函数（n为1，莫比乌斯为1 ，否者为0）

第一步转化，转成莫比乌斯

第二部调∑顺序

n

∑    ∑      ∑    μ（d）

d=1  ad<=n  bd<=m

n

=∑   μ（d） ∑      ∑    1

d=1         ad<=n  bd<=m

n

=∑  μ（d） |_ n/d _| |_ m/d _|

d=1

O（n）复杂度，k次询问就是Kn  复杂度

式子和d,n都相关

PS：d=1-min(n,m)      （假设）n最大

可以提前吧μ（d）算出

d枚举1-n,下取整n/d有多少种可能

下面分两步

（1）       1<=d<=√n      |_ n/d _|

√n种取值

（2）       √n<d<=n       n/d < √n

√n种取值

复杂度O（√n）

n

=∑  μ（d） |_ n/d _| |_ m/d _|

d=1

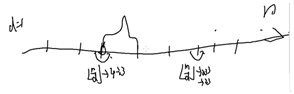
箭头表示数值发生改变

括号表示在该区间内数值不发生改变

写一下代码

求μ（d）

Mu表示前缀和

Solve  给定d,n求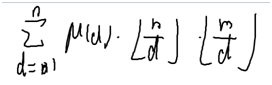

假设n<m

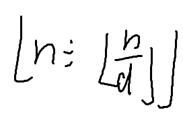是区间右端的点

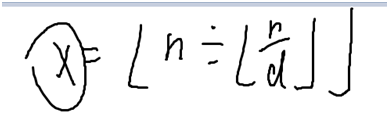
尝试证明

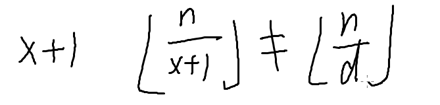
证明：

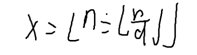
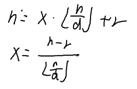
要证

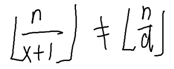
则

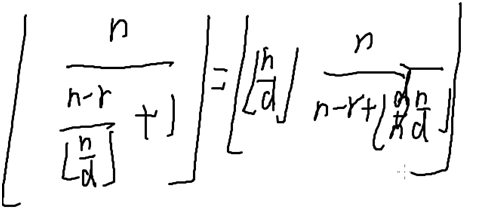
代码呈现如下：

xian_xing_shai();

for (int a=;a<=n;a++)
    sum_mu[a] = sum_mu[a-] + mu[a];

int solve(int n,int m)
{
    int ans=;
    //for (int d=1;d<=n;d++)
    //    ans += mu[d] * (n/d) * (m/d);
    for (int d=;d<=n;)
    {
        int next_d = min(
            n/(n/d),
            m/(m/d)
        );
        ans += (sum_mu[next_d] - sum_mu[d-]) * (n/d) * (m/d);
        d=next_d+;
    }
    return ans;
}

（不知道有没有用）

小结一下：

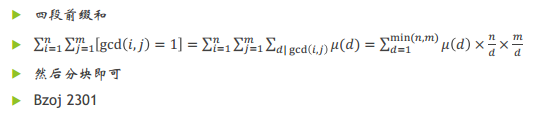
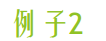
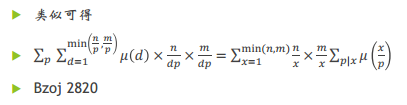
枚举P的倍数

∑化简：换个东西枚举或交换∑顺序

换成一个积性函数预处理

-----------------------------------------------------------------------------------------------------------------------------

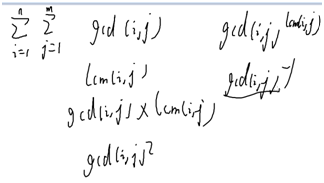
这种题目特别好出

随便换一下你就要重新推好久。。。。