CodeForces - 631C （截取法）

C. Report

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Each month Blake gets the report containing main economic indicators of the company "Blake Technologies". There are n commodities produced by the company. For each of them there is exactly one integer in the final report, that denotes corresponding revenue. Before the report gets to Blake, it passes through the hands of m managers. Each of them may reorder the elements in some order. Namely, the i-th manager either sorts first ri numbers in non-descending or non-ascending order and then passes the report to the manager i + 1, or directly to Blake (if this manager has number i = m).

Employees of the "Blake Technologies" are preparing the report right now. You know the initial sequence ai of length n and the description of each manager, that is value ri and his favourite order. You are asked to speed up the process and determine how the final report will look like.

Input

The first line of the input contains two integers n and m (1 ≤ n, m ≤ 200 000) — the number of commodities in the report and the number of managers, respectively.

The second line contains n integers ai (|ai| ≤ 109) — the initial report before it gets to the first manager.

Then follow m lines with the descriptions of the operations managers are going to perform. The i-th of these lines contains two integers ti and ri (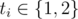, 1 ≤ ri ≤ n), meaning that the i-th manager sorts the first ri numbers either in the non-descending (if ti = 1) or non-ascending (if ti = 2) order.

Output

Print n integers — the final report, which will be passed to Blake by manager number m.

Examples

input

Copy

3 1
1 2 3
2 2

output

Copy

2 1 3 

input

Copy

4 2
1 2 4 3
2 3
1 2

output

Copy

2 4 1 3 

Note

In the first sample, the initial report looked like: 1 2 3. After the first manager the first two numbers were transposed: 2 1 3. The report got to Blake in this form.

In the second sample the original report was like this: 1 2 4 3. After the first manager the report changed to: 4 2 1 3. After the second manager the report changed to: 2 4 1 3. This report was handed over to Blake.

题意：先输入两个数n，m，再输入一个长度为n的数列，输入m个有先后关系的操作（后面的操作建立在前面操作的基础上），每个操作有两个数  t，r，t==1代表把当前前 r 个数按照非递减（递增）顺序排序，t==2代表把当前前 r 个数按照非递增（递减）顺序排序。

思路：通过题意我们可以知道，如果后面的操作中如果有 r 大于等于前面操作中的 r ，则前面的操作就相当于没有作用（假设当你递增排序排好了前r个，我如果后面再递减排序前r+1个，你前面的排序就没有用），这样可以减少部分的不必要的操作，但是如果你就按照你优化后的操作来 一 一排序，还是会超时的。

我们还要考虑怎么再去减少不必要的操作，当我们优化操作之后，得到的操作一定是递减（因为当当前的操作大于前面的操作时，前面的操作就失效了，所有当前面的操作是有效的时，当前的操作一定是小于前面所有的操作的）。当我们执行当前操作时（假设它是对前面 a 个数进行排序的），它后面一个操作（假设它是对前面 b个数进行排序的）就会对前 b 个数造成影响，那我们当前就不必对所有前 a 个数进行排序，直接对前（b+1----->a）个数进行排序就可以了（因为没有别的操作再会改变它们的顺序），这样就极大的减少了程序要运行的次数。

我们还可以对他更加的优化。

我们先对前（1--->rx）个数进行递增的排序{（ rx 为操作数中最大的那个 r ）,（假设我们已经把所有的操作存到数组 v 里面了，则v[i].r一定是大于v[i+1].r的，因为它是递减的 ）}，我们可以先直接把（rx--->n）个数直接放入答案数组（因为没有操作会对它进行影响），然后我们遍历数组 v ，

每次把位序为( v[i+1].r+1)----->v[i].r的数排序后放入答案数组，我们可以直接利用排序好的数组通过截取前面（ v[i].r - v[i+1].r ）个数 （如果它是递减的），或者是后面（ v[i].r - v[i+1].r ）个数 （如果它是递增的）。（因为每次的排序都会把当前最小的或者最大的数放在数组最后）具体请看代码。

对于这个样例

6 4
1 5 3 7 6 8
2 2
2 5
1 3
2 2
进行操作优化后得到的操作数组为
v[0].r=5;
v[1].r=3;
v[2].r=2
对于v[0]
它先对前5个要进行递减排序，而第六个数可以直接写进答案数组
ans=  _  _  _ _ _ 8
我们可以直接先对前五个数先进行递增排序
有序数组= 1 3 5 6 7

因为v[1].r==3，则第4,5个数不会被影响，而v[0]又是递减排序的，所以我们可以倒着截取有序数组前面第一和第二个数
ans=  _  _  _  3 1 8

有序数组= 1 3 5 6 7（红色代表已经使用的数字）

然后对于v[1].r=3，v[2].r=2，则第3个数不会被影响，而v[1]又是递增排序的，所以我们可以直接截取有序数组后面第一个数
ans= _ _ 7 1 3 8

有序数组= 1 3 5 6 

对于v[2].r==2,它后面已经没有操作可以影响它，而它又是递减排序的，，所以我们可以倒着把有序数组剩下的两个数字放入答案数组

我们可以直接把它放入答案数组
ans= 6 5 7 1 3 8

有序数组= 1 3 5 6 7

#include<cstdio>
#include<algorithm>
#include<vector>
using namespace std;
struct st{
	int t;
	int r;
};
vector<st> v;
int s[200010];
int ans[200010];
int main(){
	int n,m;
	int i,j,k;
	int mx=0;
	st a;
	int lg;
	scanf("%d%d",&n,&m);
	for(i=0;i<n;i++)
	scanf("%d",&s[i]);
	for(i=0;i<m;i++){
		scanf("%d%d",&a.t,&a.r);
		lg=1;
		for(j=v.size()-1;j>=0&≶j--){//优化操作数
			if(v[j].r<=a.r)//优化的条件
			v.pop_back();
			else
			lg=0;//如果a.r现在就比v[j].r小了，那它一定比前面的v[j].r小，因为数组v是递减的，这样可以避免多余的计算而导致超时
		}
		v.push_back(a);
	}
	for(i=v[0].r;i<n;i++){//先放入不会被排序影响的数字
		ans[i]=s[i];
	}
	int l=0,r=v[0].r;//表示有序数组还没被截取的那段数列的右端 ，初始左边为0，右边为v[0].r
	sort(s,s+v[0].r);//有序数组
	for(i=0;i<v.size()-1;i++){
		if(v[i].t==1){//递增
			k=0;
			for(j=v[i+1].r;j<v[i].r;j++){
				ans[j]=s[r-v[i].r+v[i+1].r+k];
				k++;
			}
			r-=k;//表示有序数组还没被截取的那段数列的右端
		}
		else if(v[i].t==2){//递减
			k=0;
			for(j=v[i].r-1;j>=v[i+1].r;j--){
				ans[j]=s[l+k];
				k++;
			}
			l+=k;//表示有序数组还没被截取的那段数列的左端
		}
	}
	k=0;
	//printf("%d %d\n",l,r);
	if(v[i].t==1)//处理最小的那组操作
	for(j=0;j<v[i].r;j++){
		ans[j]=s[r-v[i].r+k];
		k++;
	}
	else
	for(j=v[i].r-1;j>=0;j--){
		ans[j]=s[l+k];
		k++;
	}

	printf("%d",ans[0]);
	for(i=1;i<n;i++)
	printf(" %d",ans[i]);
	printf("\n");
	return 0;
}