2018ACM-ICPC南京区域赛---AJGIDKM

含【最小球覆盖】【最大流isap】模板。

题面pdf

https://codeforc.es/gym/101981/attachments/download/7891/20182019-acmicpc-asia-nanjing-regional-contest-en.pdf

G---Pyramid【数论】【规律】【递推式】

题意：

度为$n$的Pyramid是一个由$\frac{n(n+1)}{2}$个三角形组成大三角形。比如度为3的Pyramid是下面这样子。

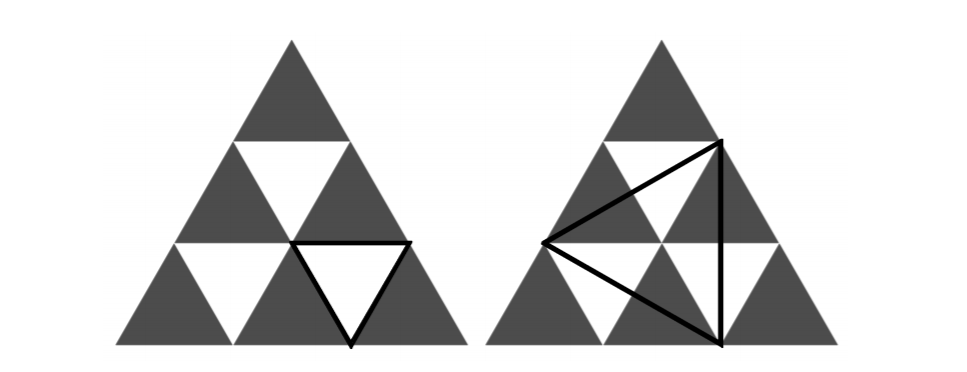
现在由这些顶点组成等边三角形，问有多少个。

思路：

zyn先放到坐标系里打了个表，然后发现差的差是一个等差数列....

于是就可以有递推关系式了。矩阵快速幂T了

所以只能解方程，把系数解出来。

注意取模求逆元！

 #include<bits/stdc++.h>
 using namespace std;
 typedef long long ll;
 const ll mod=1e9+;
 ll n;
 ll fpow(ll a,ll n)
 {
     ll res=,base=a%mod;
     while(n)
     {
         if(n&) res*=base, res%=mod;
         base*=base, base%=mod;
         n>>=;
     }
     return res%mod;
 }
 ll inv(ll a){return fpow(a,mod-);}
 int main()
 {
     int T;
     cin>>T;
     while(T--)
     {
         scanf("%I64d",&n);
         ll ans=;
         ans+=fpow(n,), ans%=mod;
         ans+=*fpow(n,)%mod, ans%=mod;
         ans+=*fpow(n,)%mod, ans%=mod;
         ans+=*n%mod, ans%=mod;
         ans*=inv(), ans%=mod;
         printf("%I64d\n",ans);
     }
 }

I---Magic Potion【网络流】

题意：

有$n$个英雄，$m$只怪物。每个英雄可以杀某些指定的怪物，但是他们只能杀一次。现在有$k$瓶药水，喝了一瓶药水就可以多杀一只怪物，但是每个英雄最多只能喝一瓶。问他们最多可以杀多少怪物。

思路：

想dp想了半天想不出来。丢给zyn他直接就说是网络流。噢好有道理。

每个英雄和怪物之间有一条权值为1的边，源点和英雄有一个权值为1的边，怪物和汇点有权值唯一的边。

这样跑出来的最大流是不考虑喝药水的情况的答案。

现在可以喝药水了，相当于多了一个节点，源点到这个节点的边权值是k，然后这个节点和每个英雄有权值是1的边。

相当于给$k$个英雄多了一条1的流量，又限制了每个英雄只能喝一瓶。

听说Dinic T了，所以后来自己直接套的isap的板子。【其实还并不很熟网络流】

 #include<iostream>
 //#include<bits/stdc++.h>
 #include<cstdio>
 #include<cmath>
 #include<cstdlib>
 #include<cstring>
 #include<algorithm>
 #include<queue>
 #include<vector>
 #include<set>
 #include<climits>
 #include<map>
 using namespace std;
 typedef long long LL;
 #define N 100010
 #define pi 3.1415926535
 #define inf 0x3f3f3f3f
 
 const int maxn = ;
 int n, m, k;
 struct edge{
     int v, w, nxt;
 }e[maxn* maxn +  * maxn];
 int h[maxn * ], tot;
 int gap[maxn * ], last[maxn * ], d[maxn * ], que[maxn * ], ql, qr;
 
 void addedge(int u, int v, int w)
 {
     e[++tot] = (edge){v, w, h[u]};
     h[u] = tot;
     e[++tot] = (edge){u, , h[v]};
     h[v] = tot;
 }
 
 void init(int s, int t)
 {
     memset(gap, , sizeof(gap));
     memset(d, , sizeof(d));
     ++gap[d[t] = ];
     for(int i = ; i <= n + m + ; i++){
         last[i] = h[i];
     }
     que[ql = qr = ] = t;
     while(ql <= qr){
         int x = que[ql++];
         for(int i = h[x], v = e[i].v; i; i = e[i].nxt, v = e[i].v){
             if(!d[v]){
                 ++gap[d[v] = d[x] + ], que[++qr] = v;
             }
         }
     }
 }
 
 int aug(int x, int s, int t, int mi)
 {
     if(x == t)return mi;
     int flow = ;
     for(int &i = last[x], v = e[i].v; i; i = e[i].nxt, v = e[i].v){
         if(d[x] == d[v] + ){
             int tmp = aug(v, s, t, min(mi, e[i].w));
             flow += tmp, mi -= tmp, e[i].w -= tmp, e[i ^ ].w += tmp;
             if(!mi)return flow;
         }
     }
     if(!(--gap[d[x]]))d[s] = n + m + ;
     ++gap[++d[x]], last[x] = h[x];
     return flow;
 }
 
 int maxflow(int s, int t)
 {
     init(s, t);
     int ret = aug(s, s, t, inf);
     while(d[s] <= n + m + )ret += aug(s, s, t, inf);
     return ret;
 }
 
 /*void addedge(int u,int v,int w) {
     e[++tot]=(edge){v,w,h[u]};
     h[u]=tot;
     e[++tot]=(edge){u,0,h[v]};
     h[v]=tot;
 }
 void init(int s,int t) {
     memset(gap,0,sizeof gap),memset(d,0,sizeof d),++gap[d[t]=1];
     for (int i=1;i<=n + m + 3;++i) last[i]=h[i];
     que[ql=qr=1]=t;
     while (ql<=qr) {
         int x=que[ql++];
         for (int i=h[x],v=e[i].v;i;i=e[i].nxt,v=e[i].v) if (!d[v]) ++gap[d[v]=d[x]+1],que[++qr]=v;
     }
 }
 int aug(int x,int s,int t,int mi) {
     if (x==t) return mi;
     int flow=0;
     for (int &i=last[x],v=e[i].v;i;i=e[i].nxt,v=e[i].v) if (d[x]==d[v]+1) {
         int tmp=aug(v,s,t,min(mi,e[i].w));
         flow+=tmp,mi-=tmp,e[i].w-=tmp,e[i^1].w+=tmp;
         if (!mi) return flow;
     }
     if (!(--gap[d[x]])) d[s]=n + m + 4;
     ++gap[++d[x]],last[x]=h[x];
     return flow;
 }
 int maxflow(int s,int t) {
     init(s,t);
     int ret=aug(s,s,t,inf);
     while (d[s]<=n + m + 3) ret+=aug(s,s,t,inf);
     return ret;
 }*/
 
 int main()
 {
     while(scanf("%d%d%d", &n, &m, &k) != EOF){
         //init(1, n+ m + 3);
         tot = ;
         memset(h, , sizeof(h));
         int s = , t = n + m + ;
         addedge(s, , k);
         for(int i = ; i <= n; i++){
             addedge(s,  + i, );
             addedge(,  + i, );
             int t;
             scanf("%d", &t);
             for(int j = , mon; j < t; j++){
                 scanf("%d", &mon);
                 addedge( + i,  + n + mon, );
             }
         }
         for(int i = ; i <= m; i++){
             addedge( + n + i, t, );
         }
         printf("%d\n", maxflow(s, t));
     }
 
     return ;
 }

D---Country Meow【最小球覆盖】

题意：

三维空间中有$n$个点，现在要在空间中找一个点，使得他到这$n$个点最远的距离最小。

思路：

就是一个最小球覆盖的板子题。找的模拟退火的板子cf过不了了。

用的三分的板子直接就过了。

#include<iostream>
//#include<bits/stdc++.h>
#include<cstdio>
#include<cmath>
#include<cstdlib>
#include<cstring>
#include<algorithm>
#include<queue>
#include<vector>
#include<set>
#include<climits>
#include<map>
using namespace std;
typedef long long LL;
#define N 100010
#define pi 3.1415926535
#define inf 0x3f3f3f3f
 
const int maxn = ;
const double eps = 1e-;
typedef struct {double p[];}point;
point a[maxn];
int n;
double cal(point now)
{
    double ans=0.0;
    for(int i=;i<n;i++)
        ans=max(ans,sqrt((a[i].p[]-now.p[])*(a[i].p[]-now.p[])+(a[i].p[]-now.p[])*(a[i].p[]-now.p[])+(a[i].p[]-now.p[])*(a[i].p[]-now.p[])));
    return ans;
}
point del(point now,int cnt)
{
    if(cnt>=)
        return now;
    double r=,l=-;
    double dr,dl;
    point tp1,tp2,ans1,ans2,ans;
    tp1=tp2=ans=now;
    while(r-l>eps)
    {
        dr=(*r+l)/;
        dl=(*l+r)/;
        tp1.p[cnt]=dl;
        tp2.p[cnt]=dr;
        ans1=del(tp1,cnt+);
        ans2=del(tp2,cnt+);
        if(cal(ans1)>cal(ans2))
        {
            l=dl;
            ans=ans1;
        }
        else
        {
            r=dr;
            ans=ans2;
        }
    }
    return ans;
}
 
int main()
{ // freopen("t.txt","r",stdin);
    //ios::sync_with_stdio(false);
    //double ans;
    while(~scanf("%d", &n))
    {
        for(int i=; i<n; i++)
            //cin>>node[i].x>>node[i].y>>node[i].z;
            scanf("%lf%lf%lf",&a[i].p[],&a[i].p[],&a[i].p[]);
        //minball(n);
        //cout<<ans<<endl;
        point ans;
        printf("%.7f\n",cal(del(ans, )));
    }
    return ;
}

K---Kangaroo Puzzle

题意：

思路：

这题代码可不能折叠啊。队友太强了！

 #include<stdio.h>
 #include<string.h>
 #include <bits/stdc++.h>
 
 using namespace std;
 const int MAX_N = ;
 char c[] = {'L', 'R', 'U', 'D'};
 
 int main()
 {
     int N, M;
     cin >> N >> M;
     string s;
     for (int i = ; i <= N; i++)
         cin >> s;
     int cnt = ;
     srand();
     while (cnt++ < ) {
         printf("%c", c[rand()%]);
     }
     puts("");
     return ;
 }

M---Mediocre String Problem【manacher】【exKMP】

题意：

有一个串$S$，一个串$T$。现在要在$S$中选一段$S[i,j]$，和$T$中的$T[1,k]$拼起来是一串回文。问有多少种不同的三元组$(i,j,k)$

思路：

详细题解见：https://www.cnblogs.com/wyboooo/p/9982651.html

 #include<iostream>
 //#include<bits/stdc++.h>
 #include<cstdio>
 #include<cmath>
 //#include<cstdlib>
 #include<cstring>
 #include<algorithm>
 //#include<queue>
 #include<vector>
 //#include<set>
 //#include<climits>
 //#include<map>
 using namespace std;
 typedef long long LL;
 #define N 100010
 #define pi 3.1415926535
 #define inf 0x3f3f3f3f
 
 const int maxn = 1e6 + ;
 char s[maxn], ss[maxn * ], t[maxn], s_rev[maxn];
 LL pre[maxn * ];
 int lens, lent, p[maxn * ];
 
 int init()
 {
     ss[] = '$';
     ss[] = '#';
     int lenss = ;
     for(int i = ; i < lens; i++){
         ss[lenss++] = s[i];
         ss[lenss++] = '#';
     }
     ss[lenss] = '\0';
     return lenss;
 }
 
 void manacher()
 {
     int lenss = init();
     int id, mx = ;
     for(int i = ; i < lenss; i++){
         if(i < mx){
             p[i] = min(p[ * id - i], mx - i);
         }
         else{
             p[i] = ;
         }
         while(ss[i - p[i]] == ss[i + p[i]])p[i]++;
         if(mx < i + p[i]){
             id = i;
             mx = i + p[i];
         }
     }
 }
 
 int nxt[maxn],ex[maxn]; //ex数组即为extend数组
 //预处理计算next数组
 void GETNEXT(char *str)
 {
     int i=,j,po,len=strlen(str);
     nxt[]=len;//初始化next[0]
     while(str[i]==str[i+]&&i+<len)//计算next[1]
     i++;
     nxt[]=i;
     po=;//初始化po的位置
     for(i=;i<len;i++)
     {
         if(nxt[i-po]+i<nxt[po]+po)//第一种情况，可以直接得到next[i]的值
         nxt[i]=nxt[i-po];
         else//第二种情况，要继续匹配才能得到next[i]的值
         {
             j=nxt[po]+po-i;
             if(j<)j=;//如果i>po+nxt[po],则要从头开始匹配
             while(i+j<len&&str[j]==str[j+i])//计算next[i]
             j++;
             nxt[i]=j;
             po=i;//更新po的位置
         }
     }
 }
 //计算extend数组
 void EXKMP(char *s1,char *s2)
 {
     int i=,j,po,len=strlen(s1),l2=strlen(s2);
     GETNEXT(s2);//计算子串的next数组
     while(s1[i]==s2[i]&&i<l2&&i<len)//计算ex[0]
     i++;
     ex[]=i;
     po=;//初始化po的位置
     for(i=;i<len;i++)
     {
         if(nxt[i-po]+i<ex[po]+po)//第一种情况，直接可以得到ex[i]的值
         ex[i]=nxt[i-po];
         else//第二种情况，要继续匹配才能得到ex[i]的值
         {
             j=ex[po]+po-i;
             if(j<)j=;//如果i>ex[po]+po则要从头开始匹配
             while(i+j<len&&j<l2&&s1[j+i]==s2[j])//计算ex[i]
             j++;
             ex[i]=j;
             po=i;//更新po的位置
         }
     }
 }
 
 int main()
 {
 
     while(scanf("%s", s) != EOF){
         scanf("%s", t);
         lens = strlen(s);
         lent = strlen(t);
         for(int i = ; i <= lens *  + ; i++){
             pre[i] = ;
             p[i] = ;
             ex[i] = ;
         }
         manacher();
         for(int i = lens * ; i >= ; i--){
             int x = i / ;
             pre[x]++;
             pre[x - (p[i] / )]--;
         }
         for(int i = lens; i >= ; i--){
             pre[i] += pre[i + ];
         }
 
         for(int i = ; i <= lens; i++){
             s_rev[i] = s[lens -  - i];
         }
         EXKMP(s_rev, t);
         LL ans = ;
         /*for(int i = 1; i <= lens; i++){
             cout<<pre[i]<<" "<<ex[i]<<endl;
         }*/
         for(int i = ; i <= lens; i++){
             //if(ex[lens - i + 1])
             ans += 1LL * ex[lens - i + ] * pre[i];
         }
         printf("%I64d\n", ans);
     }
     return ;
 }

J---Prime Game【数论】

题意：

给定$n$个数，$fra(i,j)$表示第$i$个数到第$j$个数相乘的值的不同质因子个数，求$\sum_{i=1}^{n} \sum_{j=i}^{n}fra(i,j)$

思路：

预处理把区间内的所有质数筛出来。

然后枚举每个数的质因子，找到这个质因子对答案的贡献。

每次都找到这个质因子上一次出现的位置，那么他对这段区间都是有贡献的。

 #include <bits/stdc++.h>
 
 using namespace std;
 typedef long long ll;
 const int MAX_N = 1e6 + ;
 
 int prime[MAX_N+];
 void getPrime()
 {
     memset(prime, , sizeof prime);
     for (int i = ; i <= MAX_N; i++) {
         if (!prime[i]) prime[++prime[]] = i;
         for (int j = ; j <= prime[] && prime[j] <= MAX_N/i; j++) {
             prime[i*prime[j]] = true;
             if (i%prime[j] == )
                 break;
         }
     }
 }
 
 int a[MAX_N];
 int pre[MAX_N];
 int main()
 {
     getPrime();
     int N;
     cin >> N;
     memset(pre, , sizeof pre);
     for (int i = ; i <= N; i++) {
         scanf("%d", a+i);
     }
 
     ll ans = ;
     for (int i = ; i <= N; i++) {
         for (int j = ; prime[j] <= a[i]/prime[j]; j++) {
             ll curp = prime[j];
             if (a[i] % prime[j] == ) {
                 ll l = i - pre[curp];
                 ll r = N-i+;
                 ans += l*r;
                 pre[curp] = i;
                 while (a[i]%curp == )
                     a[i] /= curp;
             }
         }
         if (a[i] > ) {
             ll curp = a[i];
             ll l = i - pre[curp];
             ll r = N-i+;
             ans += l*r;
             pre[curp] = i;
             while (a[i]%curp == )
                 a[i] /= curp;
         }
     }
     cout << ans << endl;
     return ;
 }
 /*
 10
 99 62 10 47 53 9 83 33 15 24
 */

A---Adrien and Austin【博弈论】

题意：

有$n$个石头并有编号，每次最多可以取$k$个最少取$1$个连续的石头，两个人轮流取，谁不能取了就输了。

思路：

刚开始没看到连续的，想半天都是错的。

如果是连续的话，情况就比较简单了。

先手对于任意的一段连续的$n$都可以把他取成大小相等的两段。后手在任意一段取，先手都可以在另一段对称的取。所以先手必胜。

当$n$是奇数，$k$是$1$的时候，先手没办法取出这样的两段。所以后手能赢。$n$为$0$后手也能赢。

 #include <bits/stdc++.h>
 
 using namespace std;
 const int MAX_N = 1e6 + ;
 string s[] = {"Adrien", "Austin"};
 
 int main()
 {
     int N, K;
     cin >> N >> K;
     if (N == )
         cout << s[] << endl;
     else if (K ==  && N% == ) {
         cout << s[] << endl;
     }
     else {
         cout << s[] << endl;
     }
     return ;
 }