512字节纠错1位的ECC校验码生成演示

Flash型号：

NandFlash型号：TC58NVG2S3ETA00

pagesize: 2KB

oobsize  : 64B

blocksize : 128K

关于ECC可以参考：http://www.cnblogs.com/pengdonglin137/p/3438001.html，其中介绍了256B纠错1位的ECC生成算法，而这里的512B跟它的方法类似。

这里有一个EXCEL表格，它是对下面将要分析的算法的动态演示，只需要更改其中的16*16的表格中的数字，相应的ECC会自动计算出来。我将结合EXCEL和代码一块解释。

#include <stdio.h>
#include <unistd.h>
#include <stdlib.h>
#include <fcntl.h>

#include <sys/types.h>
#include <sys/stat.h>

#include "xarina_images.h"

typedef unsigned char u_char;
typedef unsigned short u_word;

/*
 * Pre-calculated 256-way 1 byte column parity
 */
static u_char nand_ecc_precalc_table[] = {
    0x00, 0xD5, 0xD6, 0x03, 0xD9, 0x0C, 0x0F, 0xDA, 0xDA, 0x0F, 0x0C, 0xD9, 0x03, 0xD6, 0xD5, 0x00,
    0xE5, 0x30, 0x33, 0xE6, 0x3C, 0xE9, 0xEA, 0x3F, 0x3F, 0xEA, 0xE9, 0x3C, 0xE6, 0x33, 0x30, 0xE5,
    0xE6, 0x33, 0x30, 0xE5, 0x3F, 0xEA, 0xE9, 0x3C, 0x3C, 0xE9, 0xEA, 0x3F, 0xE5, 0x30, 0x33, 0xE6,
    0x03, 0xD6, 0xD5, 0x00, 0xDA, 0x0F, 0x0C, 0xD9, 0xD9, 0x0C, 0x0F, 0xDA, 0x00, 0xD5, 0xD6, 0x03,
    0xE9, 0x3C, 0x3F, 0xEA, 0x30, 0xE5, 0xE6, 0x33, 0x33, 0xE6, 0xE5, 0x30, 0xEA, 0x3F, 0x3C, 0xE9,
    0x0C, 0xD9, 0xDA, 0x0F, 0xD5, 0x00, 0x03, 0xD6, 0xD6, 0x03, 0x00, 0xD5, 0x0F, 0xDA, 0xD9, 0x0C,
    0x0F, 0xDA, 0xD9, 0x0C, 0xD6, 0x03, 0x00, 0xD5, 0xD5, 0x00, 0x03, 0xD6, 0x0C, 0xD9, 0xDA, 0x0F,
    0xEA, 0x3F, 0x3C, 0xE9, 0x33, 0xE6, 0xE5, 0x30, 0x30, 0xE5, 0xE6, 0x33, 0xE9, 0x3C, 0x3F, 0xEA,
    0xEA, 0x3F, 0x3C, 0xE9, 0x33, 0xE6, 0xE5, 0x30, 0x30, 0xE5, 0xE6, 0x33, 0xE9, 0x3C, 0x3F, 0xEA,
    0x0F, 0xDA, 0xD9, 0x0C, 0xD6, 0x03, 0x00, 0xD5, 0xD5, 0x00, 0x03, 0xD6, 0x0C, 0xD9, 0xDA, 0x0F,
    0x0C, 0xD9, 0xDA, 0x0F, 0xD5, 0x00, 0x03, 0xD6, 0xD6, 0x03, 0x00, 0xD5, 0x0F, 0xDA, 0xD9, 0x0C,
    0xE9, 0x3C, 0x3F, 0xEA, 0x30, 0xE5, 0xE6, 0x33, 0x33, 0xE6, 0xE5, 0x30, 0xEA, 0x3F, 0x3C, 0xE9,
    0x03, 0xD6, 0xD5, 0x00, 0xDA, 0x0F, 0x0C, 0xD9, 0xD9, 0x0C, 0x0F, 0xDA, 0x00, 0xD5, 0xD6, 0x03,
    0xE6, 0x33, 0x30, 0xE5, 0x3F, 0xEA, 0xE9, 0x3C, 0x3C, 0xE9, 0xEA, 0x3F, 0xE5, 0x30, 0x33, 0xE6,
    0xE5, 0x30, 0x33, 0xE6, 0x3C, 0xE9, 0xEA, 0x3F, 0x3F, 0xEA, 0xE9, 0x3C, 0xE6, 0x33, 0x30, 0xE5,
    0x00, 0xD5, 0xD6, 0x03, 0xD9, 0x0C, 0x0F, 0xDA, 0xDA, 0x0F, 0x0C, 0xD9, 0x03, 0xD6, 0xD5, 0x00,
};

#define         BIT0(x)         (((x)&0x01)>>0)
#define         BIT1(x)         (((x)&0x02)>>1)
#define         BIT2(x)         (((x)&0x04)>>2)
#define         BIT3(x)         (((x)&0x08)>>3)
#define         BIT4(x)         (((x)&0x10)>>4)
#define         BIT5(x)         (((x)&0x20)>>5)
#define         BIT6(x)         (((x)&0x40)>>6)
#define         BIT7(x)         (((x)&0x80)>>7)

void MakeEccTable(void)
{
    int i=;
    unsigned char xData;

    for(i=; i<; i++)
    {
        xData = ;
        if( (BIT0(i)^BIT2(i)^BIT4(i)^BIT6(i)) )   //CP0
            xData |= 0x01;
        if( (BIT1(i)^BIT3(i)^BIT5(i)^BIT7(i)) )   //CP1
            xData |= 0x02;
        if( (BIT0(i)^BIT1(i)^BIT4(i)^BIT5(i)) )   //CP2
            xData |= 0x04;
        if( (BIT2(i)^BIT3(i)^BIT6(i)^BIT7(i)) )   //CP3
            xData |= 0x08;
        if( (BIT0(i)^BIT1(i)^BIT2(i)^BIT3(i)) )   //CP4
            xData |= 0x10;
        if( (BIT4(i)^BIT5(i)^BIT6(i)^BIT7(i)) )   //CP5
            xData |= 0x20;
        if( (BIT0(i)^BIT1(i)^BIT2(i)^BIT3(i)^BIT4(i)^BIT5(i)^BIT6(i)^BIT7(i)) )
        {
            xData |= 0x40;
            xData |= 0x80;
        }

        nand_ecc_precalc_table[i] = xData;

    }
}

/*
 * nand_calculate_ecc - [NAND Interface] Calculate 3-byte ECC for 512-byte block
 * @buf:        raw data
 * @ecc:        buffer for ECC
 * @size:       the number of bytes to generate ECC
 *
 * size 应该是一个偶数，比如512、32
 */
int nand_calculate_ecc(u_char *buf, u_char *ecc, int size )
{
    u_char idx, reg1, reg2, reg3, tmp1, tmp2;
    int i;

    u_word *data = (u_word *)buf;

    reg1 = reg2 = reg3 = 0xff;

    for(i=; i<(size/); i++)
    {
        idx = nand_ecc_precalc_table[*data & 0xff];
        reg1 ^= (idx & 0x7f);
        idx = nand_ecc_precalc_table[(*data>>) & 0xff];
        reg1 ^= (idx & 0xBf);

        if((nand_ecc_precalc_table[*data & 0xff] ^ nand_ecc_precalc_table[(*data>>) & 0xff]) & 0xc0)
        {
            reg3 ^= (u_char) i;
            reg2 ^= ~((u_char) i);
        }
        data++;
    }

    tmp1  = (reg3 & 0x80) >> ; /* B7 -> B7 */
    tmp1 |= (reg2 & 0x80) >> ; /* B7 -> B6 */
    tmp1 |= (reg3 & 0x40) >> ; /* B6 -> B5 */
    tmp1 |= (reg2 & 0x40) >> ; /* B6 -> B4 */
    tmp1 |= (reg3 & 0x20) >> ; /* B5 -> B3 */
    tmp1 |= (reg2 & 0x20) >> ; /* B5 -> B2 */
    tmp1 |= (reg3 & 0x10) >> ; /* B4 -> B1 */
    tmp1 |= (reg2 & 0x10) >> ; /* B4 -> B0 */

    tmp2  = (reg3 & 0x08) << ; /* B3 -> B7 */
    tmp2 |= (reg2 & 0x08) << ; /* B3 -> B6 */
    tmp2 |= (reg3 & 0x04) << ; /* B2 -> B5 */
    tmp2 |= (reg2 & 0x04) << ; /* B2 -> B4 */
    tmp2 |= (reg3 & 0x02) << ; /* B1 -> B3 */
    tmp2 |= (reg2 & 0x02) << ; /* B1 -> B2 */
    tmp2 |= (reg3 & 0x01) << ; /* B0 -> B1 */
    tmp2 |= (reg2 & 0x01) << ; /* B7 -> B0 */

    ecc[] = reg1;
    ecc[] = tmp2;
    ecc[] = tmp1;
    ecc[] = 0xff;

    return ;
}

其中nand_ecc_precalc_table数组可以通过函数MakeEccTable生成。下面是在EXCEL中的截图，是要计算ECC的512B中的前三行，通过观察可以发现，每一行有16位，即两个字节，而对于256字节纠错1位的情况，每一行应该是8位。因此我们在读取源数据的时候必须要一次读取两个字节，第一个字节作为低8位，第二个字节作为高8位，其实使用一个unsigned short型的指针变量就可以了。

如果比较死板，生搬硬套256B纠1位的算法，在制作列极性表的时候会遇到麻烦，256B纠1位的算法将从0到255，每个数的列极性先算出来，将来使用的时候直接查表，原理是异或运算的最终结果跟运算的顺序没有关系。0到255一共256个数，不多。如果按照他的做法处理512纠1位时使用的列极性表，需要事先计算0到65535的列极性，可以想象，这张表得多大！如果我们仔细观察EXCEL表格：

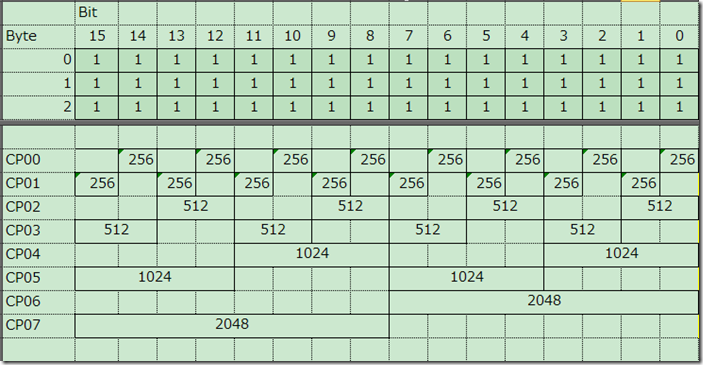
可以发现：CP00的低八位和高八位是对称的，同理CP01、CP02、CP03、CP04和CP05，他们的高低八位全都对称。同时还可以发现CP06和CP07分别计算了高低八位所有位的列极性。这下问题解决了：

只需要计算0到255就可以了，只不过计算方法有些不同，即：CP00~CP05的计算方法不变，CP06和CP07的值都是一个字节8个位全部异或的结果，即：

if( (BIT0(i)^BIT1(i)^BIT2(i)^BIT3(i)^BIT4(i)^BIT5(i)^BIT6(i)^BIT7(i)) )
        {
            xData |= 0x40;
            xData |= 0x80;
        }

从CP00到CP07正好八位，将一个字节占满，那么还有必要再填一位，用来存放他们的行极性吗?我觉得完全没有必要：得不偿失！仅仅为了那一位，列极性表占用的内存又得增加一倍，其实我们可以在查询时动态计算，不就是把低八位的列极性和高八位的列极性异或一下，看结果是否为1就可以了吗！体现在代码中就是：

if((nand_ecc_precalc_table[*data & 0xff] ^ nand_ecc_precalc_table[(*data>>) & 0xff]) & 0xc0)
        {
            reg3 ^= (u_char) i;
            reg2 ^= ~((u_char) i);
        }

这里需要注意的是异或后的结果需要再次与上0xC0，即只需要保留第6位和第7位就可以了。

由于CP06和CP07分别是低八位和高八位的列极性，在计算reg1的时候需要注意：

当计算低八位是需要先将查表得到的列极性值的第7位屏蔽，当计算高八位时，需要需要先将查表得到的列极性值的第6位屏蔽，体现在代码中就是：

        idx = nand_ecc_precalc_table[*data & 0xff];  // 低8位
        reg1 ^= (idx & 0x7f);  // 屏蔽第7位
        idx = nand_ecc_precalc_table[(*data>>) & 0xff]; //高8位
        reg1 ^= (idx & 0xBf);  // 屏蔽第6位

对于tmp1和tmp2的计算跟256纠1位没有区别。

这里还需要注意的一点是：reg1、reg2和reg3的初始值，在256纠1位中，将其初始化为了0，但是通过观察EXCEL表格，需要将其初始化为0xFF。通过观察EXCEL表格：

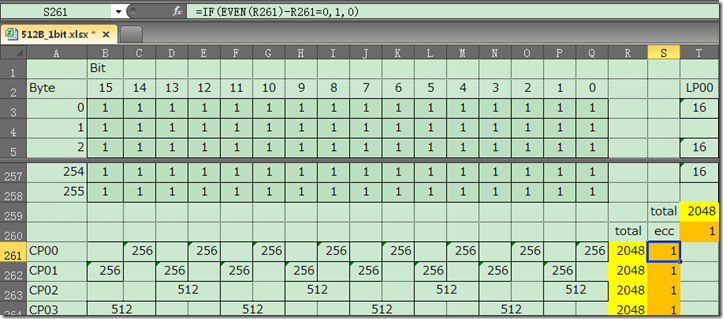
S261中的数值的计算公式是： =IF(EVEN(R261)-R261=0,1,0)

即如果R261是偶数，S261就是1，否则S261就是0。R261又是什么呢? R261 是SUM(B261:Q261)，B261是SUM(C3:C258)，……，Q261是SUM(Q3:Q258)。发现问题没有：使用异或的话，如果1的个数是偶数个，异或的结果是0，如果1的个数是奇数个，异或的结果是1，二者正好相反。

在uboot中一般都提供了nand dump命令，通过这个命令可以读到OOB中的ECC，这样可以测试自己算出的ECC是否正确，即将同样的内容一份写入NandFlash，另一份使用自己的ECC计算程序计算，将计算得到的ECC跟从NandFlash中的读到的ECC进行对比即可。

nand dump addr  其中addr需要页对齐

以上内容仅供参考。