C++描述基础算法之直接插入排序

由于此博文并不难，所以并不需要搬出C++特性的这些大山，所以就使用简单的C++代码描述了。^_^

直接插入排序是一种简单的插入排序法，所以适用于少量数据的排序，直接插入排序是比较稳定的一种排序算法。

其基本思想是：把待排序的纪录按其关键码值的大小逐个插入到一个已经排好序的有序序列中，直到所有的纪录插入完为止，得到一个新的有序序列。

插入排序：时间复杂度O(n^2)

直接插入排序是属于In-place sort（不占用额外内存或占用常数的内存），所以空间复杂度为O(1)。上一篇的冒泡排序同样如此

In-place sort的优点在于，当需要大量数据排序时，占用内存非常少。

步骤大概是这样的：

1.从第一个元素开始，该元素可以认为已经被排序          代码中   key = arr[i];就是这个意思 
2.取出下一个元素，在已经排序的元素序列中从后向前扫描
3.如果该元素（已排序）大于新元素，将该元素移到下一位置
4.重复步骤3，直到找到已排序的元素小于或者等于新元素的位置
5.将新元素插入到该位置后
6.重复步骤2~5

下面的图是动画演示，同样是从度娘那儿讨来的，毕竟自己不会做这种图。。。。

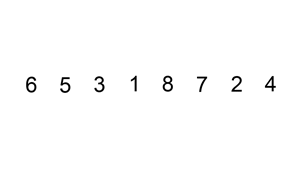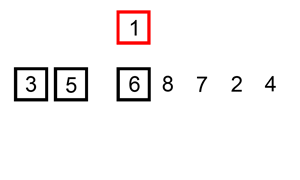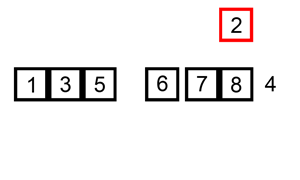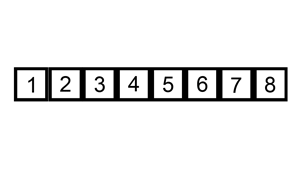
 #include <iostream>

 using namespace std;

 //// 写法1
 void insertSort_0(int arr[], int length)
 {
     int i, j, key;
     for (i = ; i < length; i++){
         key = arr[i];
         for (j = i - ; j >= ; j--){
             if (arr[j] > key) {
                 arr[j + ] = arr[j];
             }
             else
                 break;
         }
         arr[j + ] = key;
     }
 }

 //// 写法2
 void insertSort_1(int arr[], int length)
 {
     int j, key;
     for (int i = ; i < length; i++){
         key = arr[i];
         j = i - ;
         while (j >=  && arr[j] > key){
             arr[j + ] = arr[j];
             j--;
         }
         arr[j + ] = key;
     }
 }

 int main()
 {
     int iArr[] = { , , , , , , ,  };
     int len = sizeof iArr / sizeof(iArr[]);

     cout << "排序前：";
     for (int i = ; i < len; i++)    {
         cout <<  iArr[i] << " ";
     }

     cout << "\n排序后：";
     insertSort_0(iArr, len);
     for (int j = ; j < len; j++)    {
         cout << iArr[j] << " ";
     }
     cout << endl;

     system("pause");
     return ;
 }