朴素贝叶斯方法（Naive Bayes Method）

    朴素贝叶斯是一种很简单的分类方法，之所以称之为朴素，是因为它有着非常强的前提条件-其所有特征都是相互独立的，是一种典型的生成学习算法。所谓生成学习算法，是指由训练数据学习联合概率分布P(X,Y)，然后求得后验概率P(X|Y)。具体来说，利用训练数据学习P(X|Y)和p(Y)的估计，得到联合概率分布：

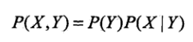
    概率估计可以是极大似然估计，或者贝叶斯估计。

    假设输入 X 为n维的向量集合，输出 Y 为类别，X 和 Y 都是随机变量。P（X,Y）是X和Y的联合概率分布，训练数据集为：

       

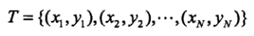
    首先，我们要明确我们求解的目标是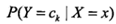：，即给定某个输入X，我们要判断其所属类别Ck。由概率论知识，我们有：

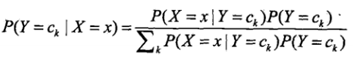
                            其中，

    代入公式得：

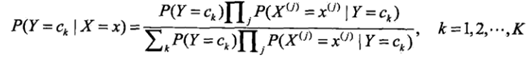
    这是朴素贝叶斯分类的基本公式。于是，朴素贝叶斯分类器可以表示为

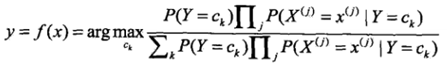
    由于，分母对所有的Ck都是相同的，所以

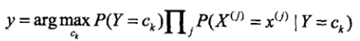
    那么如果给定一个输入 X，我们只需要找到一个类别Ck，使得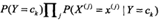最大。那么Ck，就是 X 的最佳类别了。

   

    下面我们来讲讲朴素贝叶斯法的参数估计，为什么要估计朴素贝叶斯的参数呢，这些参数是什么？首先，我们要明确。现实中，给定我们一批数据，我们就知道其分布，但是具体的数据分布的概率我们是不知道的。也就是说先验概率和条件概率我们是不知道的，这就需要我们来利用其数据的分布估计其先验概率和条件概率了。统计学习中最常用的参数估计就是极大似然估计了，这里我们也可以用贝叶斯估计，其实就是在极大似然估计基础上添加了拉普拉斯平滑（Laplace smoothing）。

    由于极大似然估计之前已经讲到过，这里公式我也没有具体来推，所以先验概率和条件概率直接给出来。

    先验概率P（Y = Ck）和条件概率的极大似然估计如下：

 

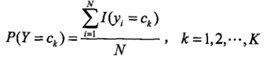
    这样，给定具体的数据，我们就可以估计其先验概率和条件概率，进而计算出后验概率得到所属类别。

    同样，贝叶斯估计和极大似然估计差不多，贝叶斯估计只是在极大似然估计上添加了一个拉普拉斯平滑。具体如下：

    条件概率的贝叶斯估计如下：

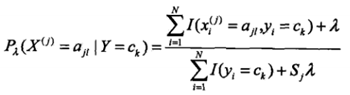
    先验概率的贝叶斯估计如下：

   

 

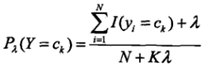
   下面来给出一个简单的朴素贝叶斯实现代码，代码比较容易理解。只是课本上给出的特征是离散的，而code里面的特征是连续的。原理上其实是一样一样的~

   1: % NAIVE BAYES CLASSIFIER

   2:  

   3: clear

   4: tic

   5: disp('--- start ---')

   6:  

   7: distr='normal';

   8: distr='kernel';

   9:  

  10: % read data

  11: White_Wine = dataset('xlsfile', 'White_Wine.xlsx');

  12: X = double(White_Wine(:,1:11));

  13: Y = double(White_Wine(:,12));

  14:  

  15: % Create a cvpartition object that defined the folds

  16: c = cvpartition(Y,'holdout',.2);

  17:  

  18: % Create a training set

  19: x = X(training(c,1),:);

  20: y = Y(training(c,1));

  21: % test set

  22: u=X(test(c,1),:);

  23: v=Y(test(c,1),:);

  24:  

  25: yu=unique(y);

  26: nc=length(yu); % number of classes

  27: ni=size(x,2); % independent variables

  28: ns=length(v); % test set

  29:  

  30: % compute class probability

  31: for i=1:nc

  32:     fy(i)=sum(double(y==yu(i)))/length(y);

  33: end

  34:  

  35: switch distr

  36:     

  37:     case 'normal'

  38:         

  39:         % normal distribution

  40:         % parameters from training set

  41:         for i=1:nc

  42:             xi=x((y==yu(i)),:);

  43:             mu(i,:)=mean(xi,1);

  44:             sigma(i,:)=std(xi,1);

  45:         end

  46:         % probability for test set

  47:         for j=1:ns

  48:             fu=normcdf(ones(nc,1)*u(j,:),mu,sigma);

  49:             P(j,:)=fy.*prod(fu,2)';

  50:         end

  51:  

  52:     case 'kernel'

  53:  

  54:         % kernel distribution

  55:         % probability of test set estimated from training set

  56:         for i=1:nc

  57:             for k=1:ni

  58:                 xi=x(y==yu(i),k);%the feature of dimension-k with respect to label yu(i)

  59:                 ui=u(:,k);

  60:                 fuStruct(i,k).f=ksdensity(xi,ui);

  61:             end

  62:         end

  63:         % re-structure

  64:         for i=1:ns

  65:             for j=1:nc

  66:                 for k=1:ni

  67:                     fu(j,k)=fuStruct(j,k).f(i);

  68:                 end

  69:             end

  70:             P(i,:)=fy.*prod(fu,2)';

  71:         end

  72:  

  73:     otherwise

  74:         

  75:         disp('invalid distribution stated')

  76:         return

  77:  

  78: end

  79:  

  80: % get predicted output for test set

  81: [pv0,id]=max(P,[],2);

  82: for i=1:length(id)

  83:     pv(i,1)=yu(id(i));

  84: end

  85:  

  86: % compare predicted output with actual output from test data

  87: confMat=myconfusionmat(v,pv);

  88: disp('confusion matrix:')

  89: disp(confMat)

  90: conf=sum(pv==v)/length(pv);

  91: disp(['accuracy = ',num2str(conf*100),'%'])

  92:  

  93: toc

   1: function confMat=myconfusionmat(v,pv)

   2:  

   3: yu=unique(v);

   4: confMat=zeros(length(yu));

   5: for i=1:length(yu)

   6:     for j=1:length(yu)

   7:         confMat(i,j)=sum(v==yu(i) & pv==yu(j));

   8:     end

   9: end

    如果想要实验数据的话，请在博客下面评论区域注明，我看到了会第一时间上传。