独树一帜的字符串匹配算法——RK算法

参加了雅虎2015校招，笔试成绩还不错，谁知初面第一题就被问了个字符串匹配，要求不能使用KMP，但要和KMP一样优，当时瞬间就呵呵了。后经过面试官的一再提示，也还是没有成功在面试现场写得。现将该算法记录如下，思想绝对是字符串匹配中独树一帜的

字符串匹配

存在长度为n的字符数组S[0...n-1]，长度为m的字符数组P[0...m-1]，是否存在i，使得S_iS_i+1...S_i+m-1等于P₀P₁...P_m-1，若存在，则匹配成功，若不存在则匹配失败。

RK算法思想

假设我们有某个hash函数可以将字符串转换为一个整数，则hash结果不同的字符串肯定不同，但hash结果相同的字符串则很有可能相同（存在小概率不同的可能）。

算法每次从S中取长度为m的子串，将其hash结果与P的hash结果进行比较，若相等，则有可能匹配成功，若不相等，则继续从S中选新的子串进行比较。

假设进行下面的匹配：

S0	S1	...	Si-m+1	Si-m+2	...	Si-1	Si	Si+1	...	Sn-1
			P0	P1		Pm-2	Pm-1

情况一、hash(S_i-m+1...S_i) == hash(P₀...P_m-1)，此时S_i-m+1...S_i与P₀...P_m-1有可能匹配成功。只需要逐字符对比就可以判断是否真的匹配成功，若匹配成功，则返回匹配成功点的下标i-m+1，若不成功，则继续取S的子串S_i-m+2...S_i+1进行hash

情况二、hash(S_i-m+1...S_i) != hash(P₀...P_m-1)，此时S_i-m+1...S_i与P₀...P_m-1不可能匹配成功，所以继续取S的子串S_i-m+2...S_i+1进行hash

可以看出，不论情况一还是情况二，都涉及一个共同的步骤，就是继续取S的子串S_i-m+2...S_i+1进行hash。如果每次都重新求hash结果的话，复杂度为O(m)，整体复杂度为O(mn)。如果可以利用上一个子串的hash结果hash(S_i-m+1...S_i)，在O(1)的时间内求出hash(S_i-m+2...S_i+1)，则可以将整体复杂度降低到线性时间

至此，问题的关键转换为如何根据hash(S_i-m+1...S_i)，在O(1)的时间内求出hash(S_i-m+2...S_i+1)

设计hash函数为：hash(S_i-m+1...S_i) = S_i-m+1*x^m-1 + S_i-m+2*x^m-2 + ... + S_i-1*x + S_i

则 hash(S_i-m+2...S_i+1) = S_i-m+2*x^m-1 + S_i-m+3*x^m-2 + ... + S_i*x + S_i+1 

　　　　　　　　　　　　= (hash(S_i-m+1...S_i) - S_i-m+1*x^m-1) * x + S_i+1

hash结果过大怎么办？对某个大素数取余数即可（经典方法），称其为HASHSIZE

所以，hash函数更新为：hash(S_i-m+1...S_i) = (S_i-m+1*x^m-1 + S_i-m+2*x^m-2 + ... + S_i-1*x + S_i) % HASHSIZE

则 hash(S_i-m+2...S_i+1) = (S_i-m+2*x^m-1 + S_i-m+3*x^m-2 + ... + S_i*x + S_i+1) % HASHSIZE 

　　　　　　　　　　　　= ((hash(S_i-m+1...S_i) - S_i-m+1*x^m-1) * x + S_i+1) % HASHSIZE

设计算法时需要注意的几点：

1、可提前计算出hash(P₀...P_m-1)和x^m-1并保存

2、char c 的取值范围为0~255，计算hash结果时会自动类型提升为int，为避免符号位扩展，使用 (unsigned int)c & 0x000000FF

3、hash(S_i-m+1...S_i) - S_i-m+1*x^m-1 的结果可能为负数，需先加上 S_i-m+1*HASHSIZE 并最后 % HASHSIZE 来保证结果非负

具体代码如下：

 #define UNSIGNED(x) ((unsigned int)x & 0x000000FF)
 #define HASHSIZE 10000019

 int hashMatch(char* s, char* p) {
     int n = strlen(s);
     int m = strlen(p);
     if (m > n || m ==  || n == )
         return -;
     // sv为S子串的hash结果，pv为字符串p的hash结果，base为x的m-1次方
     unsigned int sv = UNSIGNED(s[]), pv = UNSIGNED(p[]), base = ;
     int i, j;
     // 初始化 sv, pv, base
     for (i = ; i < m; i++) {
         pv = (pv *  + UNSIGNED(p[i])) % HASHSIZE;
         sv = (sv *  + UNSIGNED(s[i])) % HASHSIZE;
         base = (base * ) % HASHSIZE;
     }
     i = m - ;
     do {
         // 情况一、hash结果相等
         if (sv == pv) {
             for (j = ; j < m && s[i - m +  + j] == p[j]; j++)
                 ;
             if (j == m)
                 return i - m + ;
         }
         i++;
         if (i >= n)
             break;
         // O(1)时间更新S子串的hash结果
         sv = (sv + UNSIGNED(s[i - m]) * (HASHSIZE - base)) % HASHSIZE;
         sv = (sv *  + UNSIGNED(s[i])) % HASHSIZE;
     } while (i < n);

     return -;
 }

时间复杂度分析：循环复杂度O(n)，hash结果相等时的逐字符匹配复杂度为O(m)，整体时间复杂度为O(m+n)。空间复杂度为O(1)

运行时间PK

随机生成10亿字节（1024*1024*1023）的字符串保存到文件num.txt中，读出到字符串S中，P长度为1024*10字节，分别使用RK算法和KMP算法进行实验

从文件num.txt中读取字符串到S中所需时间为：

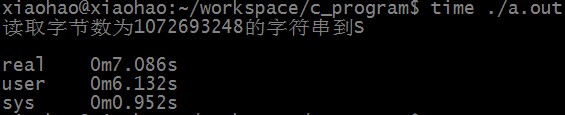
匹配成功时，RK算法匹配所需时间为：

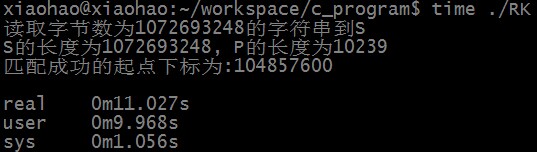
匹配成功时，KMP算法匹配所需时间为：

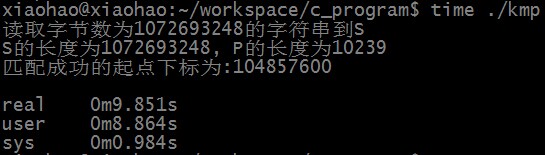
匹配不成功时，RK算法匹配所需时间为：

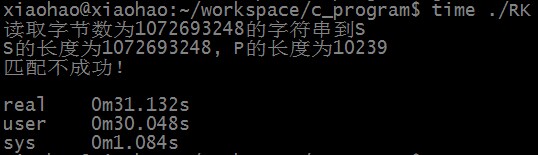
匹配不成功时，KMP算法匹配所需时间为：

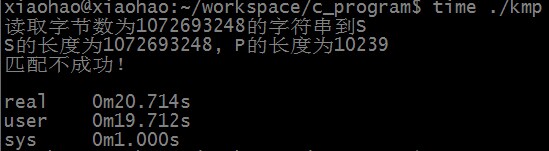
可以看出，RK算法和KMP算法均可以在线性时间内完成匹配，RK算法时间稍慢的原因主要有两点，一是数学取模运算，二是hash结果相同不一定完全匹配，需要再逐字符进行对比。统计hash结果相等但字符串不一定匹配的情况发现，匹配不成功时有105次hash结果相等但字符串不匹配的情况。S中长度为10239的子串个数大约为10亿，所以hash结果相等但不匹配的概率大约为一千万分之一（刚好约等于1/HASHSIZE），所以时间复杂度精确值应为O(n) + O(m*n/HASHSIZE)。

算法优化

在上面的测试中RK算法还是慢于KMP的，优化从两点出发：一是用其他运算代替取模运算，二是降低hash冲突。

先解决降低冲突的问题，在之前的代码中，我们使用了x=10，假设存在char值为2,20,200的三个字符a,b,c，可以发现a*1000，b*100，c*10的hash结果是相同的，也就是发生了冲突，所以取大于等于256的数做x则可以避免这种冲突。另外HASHSIZE的大小也会决定冲突发生的概率，HASHSIZE最大可以多大呢？对于unsigned int来说，总共有2^32次方个，所以可以取HASHSIZE为2^32次方。而计算机对于大于等于2^32次方的数会自动舍弃高位，其刚好等价于对2^32次方取模，即对HASHSIZE取模，所以便可以从代码中去掉取模运算。

优化后的代码如下（代码中d即上文中的x）：

 #define UNSIGNED(x) ((unsigned char)x)
 #define d 257

 int hashMatch(char* s, char* p) {
     int n = strlen(s);
     int m = strlen(p);
     if (m > n || m ==  || n == )
         return -;
     // sv为s子串的hash结果，pv为p的hash结果，base为d的m-1次方
     unsigned int sv = UNSIGNED(s[]), pv = UNSIGNED(p[]), base = ;
     int i, j;
     int count = ;
     // 初始化sv, pv, base
     for (i = ; i < m; i++) {
         pv = pv * d + UNSIGNED(p[i]);
         sv = sv * d + UNSIGNED(s[i]);
         base = base * d;
     }
     i = m - ;
     do {
         // 情况一，hash结果相等
         if (!(sv ^ pv)) {
             for (j = ; j < m && s[i - m +  + j] == p[j]; j++)
                 ;
             if (j == m)
                 return i - m + ;
         }
         i++;
         if (i >= n)
             break;
         // O(1)时间内更新sv, sv + UNSIGNED(s[i - m]) * (~base + 1)等价于sv - UNSIGNED(s[i - m]) * base
         sv = (sv + UNSIGNED(s[i - m]) * (~base + )) * d + UNSIGNED(s[i]);
     } while (i < n);

     return -;
 }

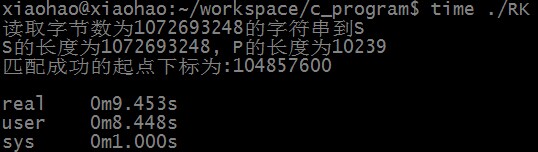
匹配成功时，优化后RK算法匹配所需时间为：

匹配不成功时，优化后RK算法匹配所需时间为：

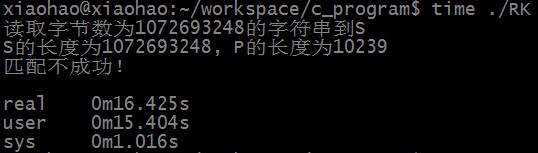
可以看出，优化后的RK算法已经在时间上优于KMP了。而且大小为2^32次方的HASHSIZE也保证了S的10亿个子串基本不会发生冲突。