CF 486D vailid set 树形DP

As you know, an undirected connected graph with n nodes and n - 1 edges is called a tree. You are given an integer d and a tree consisting of n nodes. Each node i has a value ai associated with it.

We call a set S of tree nodes valid if following conditions are satisfied:

1. S is non-empty.
2. S is connected. In other words, if nodes u and v are in S, then all nodes lying on the simple path between u and vshould also be presented in S.
3. .

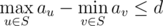Your task is to count the number of valid sets. Since the result can be very large, you must print its remainder modulo1000000007 (109 + 7).

Input

The first line contains two space-separated integers d (0 ≤ d ≤ 2000) and n (1 ≤ n ≤ 2000).

The second line contains n space-separated positive integers a1, a2, ..., an(1 ≤ ai ≤ 2000).

Then the next n - 1 line each contain pair of integers u and v (1 ≤ u, v ≤ n) denoting that there is an edge between u and v. It is guaranteed that these edges form a tree.

Output

Print the number of valid sets modulo 1000000007.

Sample test(s)

input

1 4
2 1 3 2
1 2
1 3
3 4

output

8

input

0 3
1 2 3
1 2
2 3

output

3

input

4 8
7 8 7 5 4 6 4 10
1 6
1 2
5 8
1 3
3 5
6 7
3 4

output

41

Note

In the first sample, there are exactly 8 valid sets: {1}, {2}, {3}, {4}, {1, 2}, {1, 3}, {3, 4} and {1, 3, 4}. Set{1, 2, 3, 4} is not valid, because the third condition isn't satisfied. Set {1, 4} satisfies the third condition, but conflicts with the second condition.

题意：

给定一棵树，树有点权，现在有树中有多少个有效的集合

有效的集合：

1.集合非空

2.集合是连通的，也就是说集合组成的还是一棵树

3.集合中，最大点权-最下点权<=d

这道题暑假的时候有想过，没有想出来

今天一想，其实就是一道简单的计数问题

由于n很小，O(n^2)是可以的

要max-min<=d

也就是要max<=min+d

dp[i]:i在集合里面，并且集合的最小点权就是i的点权的有效集合的个数

则：ans=sigma(dp[i])

对于一个节点root，我们考虑这个点的点权是他所在的有效集合中的最小点权,并且以root为根开始进行树形DP

如果节点i的点权>=a[root]&& 点权<=a[root]+d

我们就认为root可以扩展到i，不断扩展

并且有dp[u]=dp[u]*(1LL+dp[v])%mod

这样dfs一遍就可以在O(n)算出dp[root]了

以每一个点作为root 来dfs一遍，累加就可以得到ans了

注意一个问题：

有可能a[u]==a[v]

我们以root=u时扩展到v，并且加入了v，算了一遍

然后以root=v时扩展到u，这个时候我们如果把u加入，就会重复计算了

那么在有多个点的点权相等时，我们怎么避免重复计算，只算一次呢？

其实只要我们设一个数组vis[i][j],算第一次的时候我们把数组标记为true，后面就不再加入了

#include<cstdio>
#include<cstring>
#include<algorithm>
#include<iostream>

#define LL long long

using namespace std;

const int maxn=;
const int mod=1e9+;

LL dp[maxn];
int a[maxn];
bool vis[maxn][maxn];
int sum;
int root;

struct Edge
{
    int to,next;
};
Edge edge[maxn<<];
int head[maxn];
int tot;

void init()
{
    memset(head,-,sizeof head);
    tot=;
}

void addedge(int u,int v)
{
    edge[tot].to=v;
    edge[tot].next=head[u];
    head[u]=tot++;
}

void solve(int ,int d);

int main()
{
    init();
    int n,d;
    scanf("%d %d",&d,&n);
    for(int i=;i<=n;i++){
        scanf("%d",&a[i]);
    }
    for(int i=;i<n;i++){
        int u,v;
        scanf("%d %d",&u,&v);
        addedge(u,v);
        addedge(v,u);
    }
    solve(n,d);

    return ;
}

void dfs(int u,int pre)
{
    dp[u]=;
    for(int i=head[u];~i;i=edge[i].next){
        int v=edge[i].to;

        if(v==pre || a[v]<a[root] || a[v]>sum)
            continue;

        if(a[v]==a[root]){
            if(!vis[v][root]){
                vis[v][root]=true;
                vis[root][v]=true;
                dfs(v,u);
            }
            else
                continue;
        }
        else{
            dfs(v,u);
        }
        dp[u]=dp[u]*(1LL+dp[v])%mod;
    }
}

void solve(int n,int d)
{
    memset(vis,false,sizeof vis);
    LL ans=;
    for(int i=;i<=n;i++){
        sum=a[i]+d;
        root=i;
        dfs(root,root);
        ans=(ans+dp[root])%mod;
        ans=(ans+mod)%mod;
        //cout<<dp[root]<<endl;
    }

    printf("%I64d\n",ans);
    return ;
}