sdut 2153 Clockwise (2010年山东省第一届ACM大学生程序设计竞赛)

题目大意:

n个点，第i个点和第i+1个点可以构成向量，问最少删除多少个点可以让构成的向量顺时针旋转或者逆时针旋转。

分析：

dp很好想，dp[j][i]表示以向量ji（第j个点到第i个点构成的向量）为终点的最大顺时针/逆时针向量数。状态转移方程为 dp[j][i] = max{dp[k][j]+1}。

问题个关键是如何判断2个向量是顺时针还是逆时针。

计算几何用的知识是求叉积和点积，叉积的作用是判断两个向量的左右（顺逆），点积的作用是判断两个向量的前后。举个例子，假设有2个向量v1，v2，‘*’暂时代表叉积运算，‘·’暂时代表点积运算。叉积判定：如果v1*v2>0，则v1在v2的顺时针方向；如果v1*v2=0，则v1、v2共线；如果v1*v2<0，则v1在v2的逆时针方向。点积判定：如果v1·v2>0，则v1和v2都指向同一侧面；如果v1·v2=0，则v1和v2垂直；如果v1·v2<0，则v1和v2都指向相反的侧面。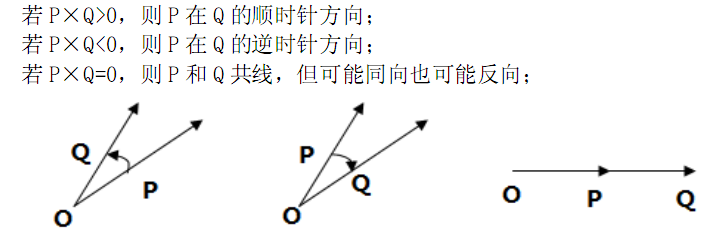

顺时针的旋转范围是(0<=T<180)，逆时针的旋转范围是(0<T<=180)，也就是说如果两条向量共线的话，顺时针旋转可以同方向（T=0），不能反方向；逆时针旋转可以反方向（T=180），不能同方向。

 #include<cstdio>
 #include<cstring>
 #include<iostream>
 #include<cmath>
 #include<algorithm>
 #include<set>
 #include<queue>
 #include<stack>
 #define MAXN 310

 using namespace std;
 int dp[MAXN][MAXN],n;
 struct Point
 {
     int x,y;
     Point (int x_=,int y_=):x(x_),y(y_) {}
 } p[MAXN];
 typedef Point Vector;
 Vector operator -(Point a,Point b)
 {
     return Vector(a.x-b.x,a.y-b.y);
 }
 int  Cross(Vector a,Vector b)//向量叉积
 {
     return a.x*b.y-a.y*b.x;
 }
 int Dot(Vector a,Vector b)//向量点乘
 {
     return a.x*b.x+a.y*b.y;
 }
 int if_shun(int i,int j,int k)//判断顺时针
 {

     Vector v1=p[i]-p[j];
     Vector v2=p[j]-p[k];
     int tem=Cross(v1,v2);
     if(tem>)
         return ;
     else if(tem<)
         return ;
     if(tem==)
     {
         int tem1=Dot(v1,v2);
         if(tem1<)
             return ;
         return ;
     }
 }
 int if_ni(int i,int j,int k)//判断逆时针
 {

     Vector v1=p[i]-p[j];
     Vector v2=p[j]-p[k];
     int tem=Cross(v1,v2);
     if(tem>)
         return ;
     else if(tem<)
         return ;
     if(tem==)
     {
         int tem1=Dot(v1,v2);//向量共线，判断一下方向
         if(tem1<)
             return ;
         return ;
     }
 }
 int puan_shun()
 {
     int ans=;
     //dp[0][1]=1;
     for(int i=; i<n; i++)
     {
         for(int j=; j<i; j++)
         {
             dp[j][i]=;
             for(int k=; k<j; k++)
             {
                 if(if_shun(i,j,k))
                     dp[j][i]=max(dp[j][i],dp[k][j]+);
             }
             ans=max(ans,dp[j][i]);
         }

     }
     return ans;
 }
 int puan_ni()
 {
     int ans=;
     //dp[0][1]=1;
     for(int i=; i<n; i++)
     {
         for(int j=; j<i; j++)
         {
             dp[j][i]=;
             for(int k=; k<j; k++)
             {
                 if(if_ni(i,j,k))
                     dp[j][i]=max(dp[j][i],dp[k][j]+);
             }
             ans=max(ans,dp[j][i]);
         }

     }
     return ans;
 }

 int main()
 {
     while(scanf("%d",&n)!=EOF&&n)
     {
         for(int i=; i<n; i++)
             scanf("%d %d",&p[i].x,&p[i].y);
         memset(dp,,sizeof(dp));
         int ans1=puan_shun();
         memset(dp,,sizeof(dp));
         int ans2=puan_ni();
         //printf("%d %d==\n",ans1,ans2);
         if(ans1==n-)
             printf("C\n");
         else if(ans2==n-)
             printf("CC\n");
         else if(ans1>=ans2)
             printf("Remove %d bead(s), C\n",n-ans1-);
         else
             printf("Remove %d bead(s), CC\n",n-ans2-);
         printf("\n");
     }
     return ;
 }