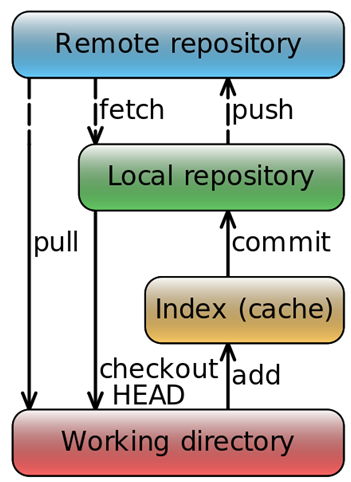
git图解
git图解的更多相关文章
- [转]git图解(3):分支操作
本文转自:https://www.jianshu.com/p/342a9f8db004 title_img.png git 的分支是它最明显的特性, 大部分人听别人推荐使用git都会听到“git分 ...
- [git]图解git常用命令
本文图解git中最常用的命令.如果你稍微理解git的工作原理,这篇文章能够让你理解的更透彻. 基本用法 约定 命令详解 Diff Commit Checkout Detached HEAD(匿名分支提 ...
- git图解:代码区域总结
本文背景,在实际项目中使用git已有一年多,发现不少同事虽然会使用常用git指令,但并不理解每个指令对应的作用原理.今天静下心总结下git 的基本理解:代码的存在区域:本文以实际项目出发,理清使用gi ...
- Git 图解剖析
git中文件内容并没有真正存储在索引(.git/index)或者提交对象中,而是以blob的形式分别存储在数据库中(.git/objects),并用SHA-1值来校验. 索引文件用识别码列出相关的bl ...
- Git 图解剖析(转)
git中文件内容并没有真正存储在索引(.git/index)或者提交对象中,而是以blob的形式分别存储在数据库中(.git/objects),并用SHA-1值来校验. 索引文件用识别码列出相关的bl ...
- ###Git 基础图解、分支图解、全面教程、常用命令###
一.Git 基础图解 转自:http://www.cnblogs.com/yaozhongxiao/p/3811130.html Git 图解剖析 git中文件内容并没有真正存储在索引(.git/in ...
- Git学习笔记(10)——搭建Git服务器
本文主要记录了Git服务器的搭建,以及一些其他的配置,和最后的小总结. Git远程仓库服务器 其实远程仓库和本地仓库没啥不同,远程仓库只是每天24小时开机为大家服务,所以叫做服务器.我们完全可以把自己 ...
- Git详解之三 Git分支
相关文档 — 更多 Git 基础培训.ppt GIT 使用经验.ppt GIT 介绍.pptx GIT 分支管理是一门艺术.docx Eclipse上GIT插件EGIT使用手册.docx git/gi ...
- 一个小时学会Git
一.版本控制概要 Git 是一种在全球范围都广受欢迎的版本控制系统.在开发过程中,为了跟踪代码,文档,项目等信息中的变化,版本控制变得前所未有的重要.但跟踪变化远远不能满足现代软件开发行业的协同需求, ...
随机推荐
- 2、Qt Project之鼠标事件监控
鼠标事件监控: 对于鼠标时间监控的相关操作,我们在简历工程的时候需要选择的是QWidget基类,不选择QMainWindow基类,如下所示: Base class:QWidget Step1:我们首先 ...
- Kafka 概念、单机搭建与使用
目录 Kafka 概念.单机搭建与使用 基本概念介绍 Topic Producer Consumer Kafka单机配置,一个Broker 环境: 配置zookeeper 配置Kafka 使用Kafk ...
- node.js爬取数据并定时发送HTML邮件
node.js是前端程序员不可不学的一个框架,我们可以通过它来爬取数据.发送邮件.存取数据等等.下面我们通过koa2框架简单的只有一个小爬虫并使用定时任务来发送小邮件! 首先我们先来看一下效果图 差不 ...
- 使用SpringSecurity
前几天写了一个SpringBoot对拦截器的使用,在实际项目中,对一些情况需要做一些安全验证,比如在没有登录的情况下访问特定的页面应该解释的拦截处理.这一篇介绍使用SpringSecurity来做简单 ...
- CodeForces - 1016D 补零思想
题目连接: https://vjudge.net/problem/1753263/origin 其实这道题跟行列式里的分块发有点类似,但也是类似罢了. 主要的思想是每一行,每一列的第一行(或者最后一行 ...
- Java笔记(五)泛型
泛型 一.基本概念和原理 泛型将接口的概念进一步延申,“泛型”的字面意思是广泛的类型. 类.接口和方法都可以应用于非常广泛的类型,代码与它们能够操作 的数据类型不再绑定到一起,同一套代码可以应用到多种 ...
- [PA2014]Żarówki
[PA2014]Żarówki 题目大意: 有\(n(n\le5\times10^5)\)个房间和\(n\)盏灯,你需要在每个房间里放入一盏灯.每盏灯都有一定功率\(p_i\),每间房间都需要功率不小 ...
- BZOJ3565 : [SHOI2014]超能粒子炮
若$a\leq 1000$,则整个$f$数列会形成$O(a)$段公差为$a$的等差数列. 否则$a^{-1}\leq 1000$,设$ai+b=f(i)$,那么有$i=a^{-1}f(i)-ba^{- ...
- Flask 三方组件 WTForms
WTForms是一个支持多个web框架的form组件,主要用于对用户请求数据进行验证 from flask import Blueprint from flask import request fro ...
- 创建触发器(trigger)
创建触发器 DROP TRIGGER IF EXISTS `ins_table_name`; DELIMITER ;; CREATE TRIGGER `ins_table_name` AFTER IN ...
